Машина переменного тока (асинхронная)

Математическое описание обобщенной асинхронной машины

Токи и напряжения фаз статора (ротора тоже) асинхронного двигателя можно представить в виде пространственного вектора [4], что приводит к сокращению числа и упрощению структуры уравнений, описывающих рабочие процессы асинхронного двигателя.

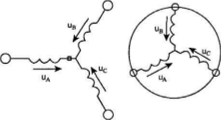
В общем случае на трёхфазной обмотке статора действует трёхфазная система напряжений:

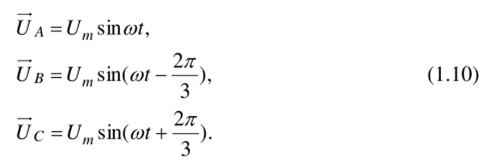
Суммарный вектор напряжения можно представить в виде:

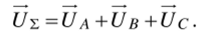
Если ось А координатной системы А, В, С совместить с вещественной осью комплексной плоскости, расположенной перпендикулярно валу машины, то пространственный (обобщенный) вектор напряжения на обмотках статора асинхронного двигателя определяется уравнением:

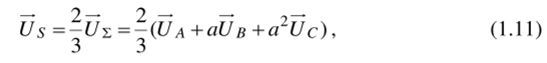
где Uл, U_в, Uс — мгновенные значения фазных напряжений (1.10); а — оператор поворота.

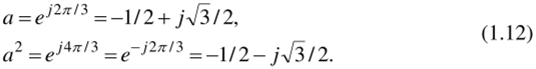
Подставим в формулу для пространственного вектора (1.11) выражения (1.10) и (1.12):

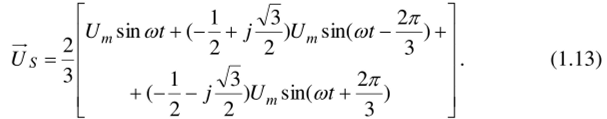
При преобразовании полученного выражения использованы следующие соотношения:

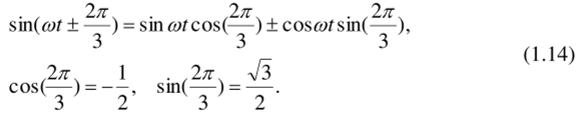
После преобразования (1.13) получим:

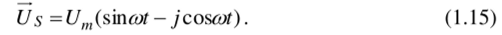
Приведем полученное комплексное выражение к стандартной тригонометрической форме, заменив sinсоt — cos (ж/2-ajt) и coscot=sin (ic/2-cot)

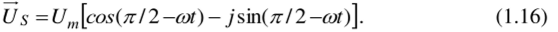
Переведем полученное выражение из тригонометрической формы в показательную:

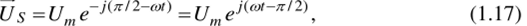
что указывает на возникновение постоянной по амплитуде U_m пространственной волны напряжения, вращающейся в положительном направлении с частотой со. Начальное положение пространственного вектора при t-О соответствует углу (-л/2), что позволяет получить его проекции при вращении на оси А, В, С, изменяющиеся в соответствии с формулами (1.10).

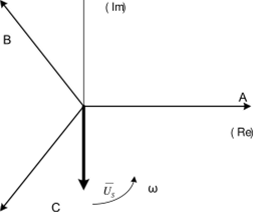
Рис. 1.38. Пространственный вектор напряжения

На рис. 1.38 представлена геометрическая интерпретация пространственного вектора напряжения — это вектор на комплексной плоскости с модулем (длиной) U"" вращающийся с угловой скоростью со в положительном направлении. Проекции вектора U_s на фазные оси А, В, С определяют мгновенные напряжения в фазах. Аналогично пространственными векторами можно представить все напряжения, токи и потокосцепления, входящие в уравнения, описывающие работу асинхронного двигателя.

При построении реальных систем электропривода переменного тока, как асинхронных, так и синхронных, практически всегда в систему управления включают преобразователи фаз 3/2 и 2/3 [2].

Первый (3/2) преобразовывает фазные напряжения трёхфазной системы в напряжения двухфазной системы в координатах а, /1. Отмстим, что как трёхосная координатная система А, В, С, так и двухосная а, [} являются неподвижными системами. Пространственный вектор изображает результат совместного действия трёхфазной системы токов любой эквивалентной т — фазной и, в частности, двухфазной системы. Переход к двухфазной системе в математическом отношении эквивалентен рассмотрению пространственного вектора в новой прямоугольной системе координат а, [1. Физический смысл такого преобразования координат состоит в замене реальной трёхфазной машины эквивалентной двухфазной моделью, характеризующейся тем же значением пространственного вектора. Такая замена переменных широко используется при математическом исследовании электрических машин с целью упрощения систем дифференциальных уравнений электрического равновесия статорных и роторных цепей.

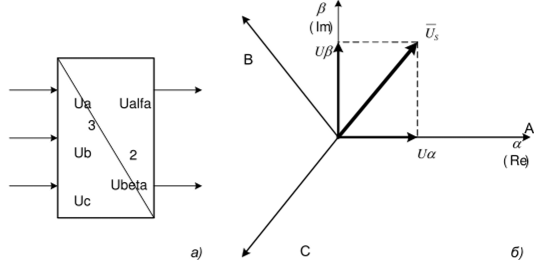
Рис. 1.39. Преобразование координат: а) условное графическое обозначение преобразователя: б) координаты

Преобразователь (3/2) осуществляет преобразование трёхфазных напряжений U_A, U_B, U_c (1.10) в двухфазные напряжения U_№ Up в соответствии с выражениями (1.11) и (1.12):

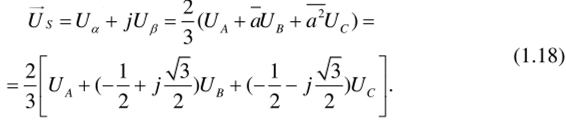
После преобразования (1.18) получим.

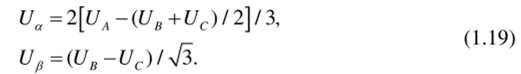
При этом следует иметь в виду, что фазная ось а прямоугольной (двухфазной) системы совмещена с фазной осью А трёхфазной системы (рис. 1.39, б).

На рис. 1.40 показана модель преобразователя (3/2) в Simulink (Matlcib) [2].

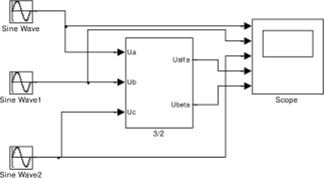
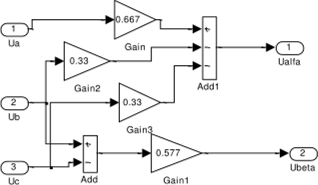
Рис. 1.40. Модель преобразоватечя (3/2) (Figl₄₀)

Амплитуда напряжения принята (/," = 1 В, частота со = 314 рад/сек (f= 50 Гц). Не трудно отметить, что пространственный вектор напряжения в координатах а, /3 описывается выражением (1.15), полученным для трёхфазной системы напряжений U =U_m(sincaf- jcoscot). Из (1.15) следует, что в двухфазной системе напряжения вычисляются, как U _а =U_ms cot и U р = -U_m coscot. Результаты расчета напряжений U_a и.

Ufj на модели позволяют сделать вывод, что пространственный вектор для трёхфазной и эквивалентной двухфазной систем одинаков и имеет выражение Us = U_me^

~'^T/2

На рис. 1.41 показан результат преобразования трёхфазиого напряжения в двухфазное.



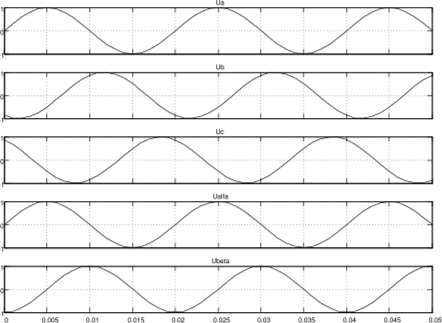
Рис. 1.41. Результаты преобразования 3-хфазной системы напряжений (U," = 1 В. /= 50 Гц) на модечи, показанной на рис. 1.40.

пространственного вектора У 5 на оси А, В. С. Выражения для фазных напряжений Ua, U _в, Uс представляют действительную часть проекции пространственного вектора Us на фазные оси А, В, С.

В соответствии с этим, имеем [2]:




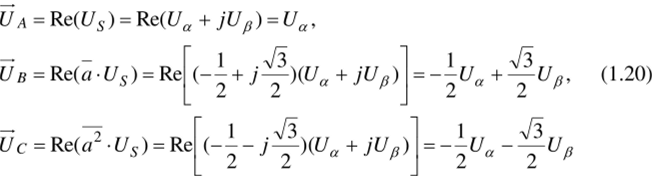
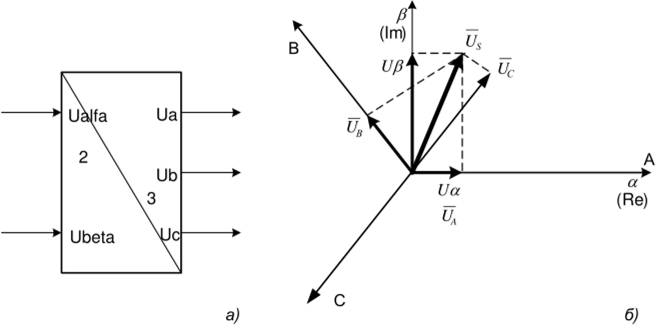
Рис. 1.42. Графическая интерпретация работы преобразователя (2/3): а) условное графическое изображение преобразователя (2/3), б) преобразование координат.

На рис. 1.42 показан процесс графического формирования мгновенного состояния векторов фазных напряжений Ua, Ug, Uc для произвольного положения пространственного вектора Us ?

Полученные выражения (1.20) использованы при разработке модели преобразователя фаз (2/3) в Simulink |2], показанной на рис. 1.43.

На рис. 1.44 показаны результаты моделирования эквивалентного обратного преобразования двухфазной системы в трёхфазную.

Так же приняты: амплитудное напряжение U_m- 1 В и частота 50 Гц. На выходе получена трёхфазная система напряжений с прямым чередованием фаз.



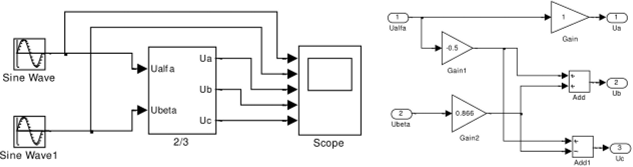
Рис. 1.43. Модель преобразователя фаз с раскрытой подсистемой 2/3 (Figl₄₃)



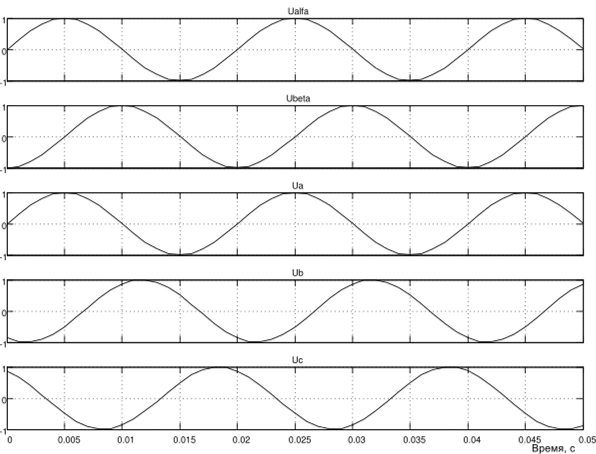
Рис. 1.44. Результаты моделирования работы преобразователя фаз (2/3)

Вращающаяся система координат в общем случае может перемещаться относительно неподвижной с произвольной скоростью со_к. Мгновенное положение такой системы координат относительно неподвижной определяется углом у между вещественными осями систем координат. Положение пространственного вектора напряжения во вращающейся системе координат можно определить путем его поворота на угол у против направления вращения. Поэтому между выражениями пространственного вектора Us в неподвижной и Usk во вращающейся системах координат имеют место следующие соотношения [2]:

Математическая основа преобразования координат поясняется на рис. 1.45.



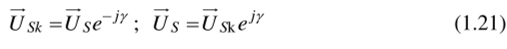
В неподвижной системе координат (а, /?) пространственный вектор напряжения может быть представлен в алгебраической и показательной форме Us=U_a + jU_p=U_me^jv.



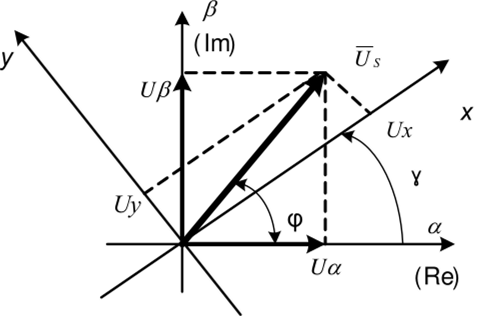
Рис. 1.45. Преобразование координат

Аналогично в системе вращающихся координат (х, у) тот же самый вектор может быть представлен в виде:



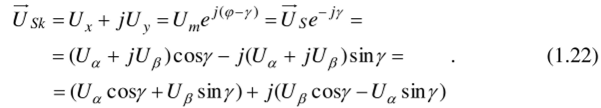
Из выражения (1.22) получаем уравнения перехода от неподвижной системы координат к вращающейся:



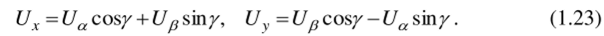
Аналогично получаем уравнения перехода от вращающейся системы координат к неподвижной с учетом (1.21):



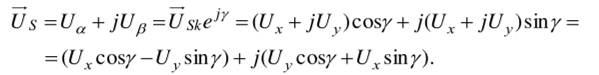
Тогда.



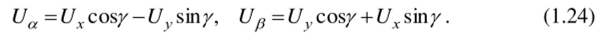
На рис. 1.46 представлена модель преобразователя неподвижной системы координат во вращающуюся, реализованную по уравнениям (1.23).



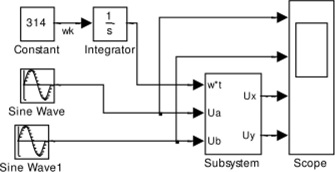
Рис. 1.46. Модель преобразователя из неподвижной системы координат во вращающуюся, схема Subsystem (Figl₄₆)



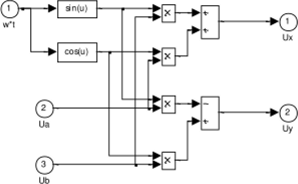
На рис. 1.47 представлены результаты моделирования. На экране осциллоскопа представлены синусоидальные напряжения Ua и Ub в неподвижной системе и постоянные напряжения Ux = 0, Uy = -1 во вращающейся, подтверждающие предположение, сделанное ниже.



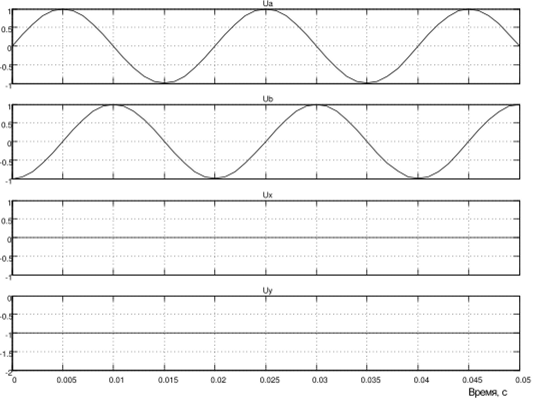
Рис. 1.47. Результаты моделирования

На вход модели поданы проекции пространственного вектора напряжения на оси (а, /?) в виде синусоидальных напряжений частоты 314рад/сек и текущий угол поворота координатной оси от блока.

Integrator. Угол y = co_kt, где w_k представляет частоту вращения системы координат. Частота вращения в рад/сек задаётся константой на входе интегратора. Следует заметить, что в этом случае на вход модели подаются синусоидальные функции времени с частотой 314 рад/сек в неподвижной системе координат и задаётся вращение координат с частотой 314 рад/сек. Следовательно, на выходах Ux, Uy должны получиться неподвижные векторы, характеризуемые постоянными величинами на выходах Ux и Uy. Преобразователь координат реализован в блоке Subsystem, содержание которого представлено на рис. 1.46.

Если частоту вращения координат со_к задать отличной от частоты входного напряжения, то на выходе преобразователя появляются синусоидальные напряжения разностной частоты со — со_к. Следовательно, пространственный вектор вращается во вращающейся системе координат с частотой (о — со_к.

Аналогичная модель строится и для преобразования переменных в вращающейся системе координат в неподвижную в соответствии с уравнениями (1.24) [2].

Па рис. 1.48 представлена модель преобразователя вращающейся системы координат в неподвижную, реализованную по уравнениям (1.24). На вход модели поданы проекции пространственного вектора напряжения на вращающиеся оси (х, у) и текущий угол поворота системы координат. На выходе модели получены составляющие пространственного вектора (Ua, Ub) в неподвижной системе координат. Преобразователь координат реализован в блоке Subsystem, содержание которого представлено на рис. 1.48.




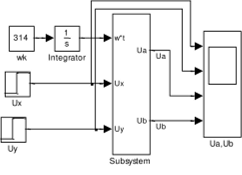
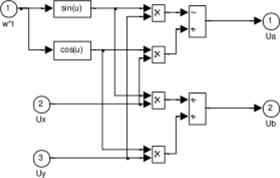
Рис. 1.48. Модель преобразователя вращающихся координат в неподвижные, схема блока Subsystem (Figl₄₈)

На рис. 1.49 представлены результаты моделирования. Напряжения U_и, U/, видны на экране осциллоскопа. Следует заметить, что в этом случае на вход интегратора подаётся сигнал частоты вращения координат 314 1/с, и на выходе получаются синусоидальные напряжения частотой 50 Гц.



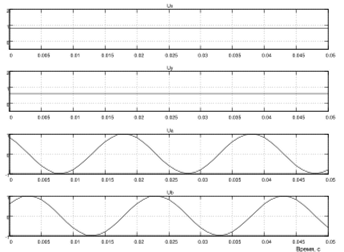
Рис. 1.49. Результат моделирования процесса преобразования вращающихся координат в неподвижные

Между выражениями пространственного вектора Us в неподвижной и U sk во вращающейся системах координат имеют место соотношения (1.21).

Второе уравнение (1.21) используется обычно для замены переменных при переходе к новой системе координат, а первое — для выражения в новой системе координат возмущающих функций, описанных переменными прежней системы.

Например, уравнение электрического равновесия цепи статора, записанное через обобщенные векторы напряжений, токов и потокосцеплений в неподвижной системе координат, имеет вид:



где Us =U_me^{J (0}" ^!; со₀ — угловая частота питающей сети.

То же уравнение в системе координат, вращающейся со скоростью ротора <�у,., когда со_к =ы_г и y = co_rt, согласно второго уравнения (1.21):



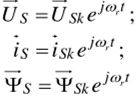
будет иметь вид:



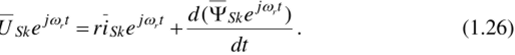
Распишем производную сложной функции.



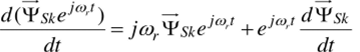
и подставим в выражение (1.26):



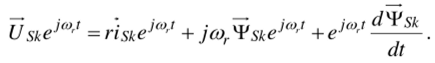
Сократив левую и правую часть полученного выражения на e^^{, окончательно получим уравнение электрического равновесия во вращающейся системе координат}



^{где (/" согласно первого выражения (1.21) следует определить как}



^{В приведенном уравнении (1.27) индекс к указывает на замену переменных в связи с переходом к новой системе координат. В дальнейшем, если переход к новой системе координат поясняется сопровождающим текстом, индекс А: для упрощения записи будет опущен. При этом пространственный вектор будет определен как выражение (1.28).}

^{В теории электромагнитных переходных процессов электрических машин применяются обычно три координатные системы, являющиеся частными случаями координатной системы, вращающейся с произвольной скоростью со_к: система координат d, q, неподвижная относительно ротора и вращающаяся вместе с ротором (со_к = со_г); система координат а, // неподвижная относительно статора (а>_к =0); система координат х, у вращающаяся в пространстве с произвольной скоростью (о_к. Замена переменных в уравнениях электрического равновесия машины производится с целью исключения периодически изменяющихся коэффициентов в уравнениях потокосцеплений. Достижение поставленной цели возможно только в том случае, если новая система координат неподвижна относительно цепей, обладающих электрической или магнитной несимметрией.}

^{Поэтому систему координат d, q, используют преимущественно для исследования режимов синхронных машин, а систему а, /? — для исследования режимов асинхронных машин. Систему координат х, у целесообразно использовать только для исследования симметричных режимов асинхронных машин, если ес применение приводит к упрощению описаний возмущающих воздействий. Например, пространственный вектор питающего двигатель напряжения в системе координат а, /? имеет вид:}



^{а при переходе к системе координат х, у, вращающейся со скоростью со_к = (о₀, это напряжение согласно (1.21), преобразуется к виду U s = U_m.}

^{Рассмотрим описание процессов в абсолютных единицах. Обобщенная асинхронная машина показана на рис. 1.50.}



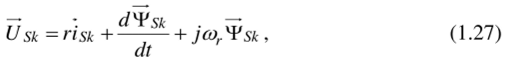
^{Рис. 1.50. Обобщенная асинхронная машина}

^{Машина содержит трехфазную обмотку на статоре и трехфазную обмотку на роторе. Обмотки статора и ротора подключены к симметричным трехфазным источникам напряжения. Уравнения равновесия э.д.с. на обмотках статора и ротора базируются на втором законе Кирхгофа [2].}



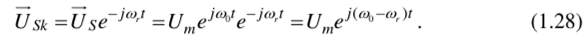
^{В уравнениях (1.29) фигурируют мгновенные напряжения, гоки и потокосцепления статора и ротора, а также активные сопротивления обмоток. Обычно обмотки выполняются симметричными, и поэтому R_a-R_b-Rc-Rs — активное сопротивление статорной обмотки, R_a — Ri, = Rс — Rr — активное сопротивление роторной обмотки.}

^{Вторым используемым законом является закон Ампера, который связывает потокосцепления обмоток с токами, протекающими по обмоткам:}



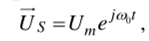
^{Уравнения для определения потокоспеплений показывают, что потокосцепление каждой обмотки зависит от токов во всех обмотках; зги зависимости проявляются через взаимоиндукцию. В уравнениях (1.30) L_Aa, Lbb, Leo L_aa, L_bb, L_cc являются собственными индуктивностями соответствующих обмоток, все остальные — взаимоиндуктивностями между соответствующими обмотками.}

^{Третьим законом, лежащим в основе анализа, является второй закон Ньютона — закон равновесия моментов на валу машины:}



^{где J (кГм2) — момент инерции на валу машины, учитывающий инерционность как самой машины, так и приведенной к валу инерционности рабочего механизма и редуктора; со_п,(рад/с) — угловая скорость вала машины; Мс (Нм) — момент сопротивления рабочего механизма, приведенный к валу, в общем случае он может быть функцией скорости и угла поворота.}

Наконец, четвертым и последним законом, лежащим в основе анализа машины, является закон, сформулированный Ленцем, как правило левой руки. Этот закон связывает векторные величины момента, потокосцепления и тока:



Отметим, что, несмотря на полное и строгое математическое описание, использование уравнений (1.29)—(1.32) для исследования машины встречает серьезные трудности.

Перечислим основные:

• — в уравнениях (1.31 и 1.32) фигурируют векторные величины, а в уравнениях (1.29 и 1.30) скалярные;
• — количество взаимосвязанных уравнений равно 16, а количество коэффициентов — 44;
• — коэффициенты взаимоиндукции между обмотками статора и ротора в уравнениях (1.30) являются функцией угла поворота ротора относительно статора, то есть уравнения (1.30) являются уравнениями с переменными коэффициентами;
• — уравнение (1.32) является нелинейным, так как в нем перемножаются переменные.

На пути упрощения математического описания асинхронной машины, да и вообще всех машин переменного тока, удачным оказался метод пространственного вектора [4], который позволил существенно упростить и сократить вышеприведенную систему уравнений; метод позволяет связать уравнения (1.29−1.32) в единую систему с векторными переменными состояния. Суть метода состоит в том, что мгновенные значения симметричных трехфазных переменных состояния (напряжения, токи, потокосцепления) можно математически преобразовать так, чтобы они были представлены одним пространственным вектором.

Для преобразования уравнений (1.29) в мгновенных значениях к уравнениям в пространственных векторах умножим их на выражения: первые уравнения для фаз А и а на 2/3, вторые для фаз В и b — на 2/3а, третьи для фаз С и с — на 2/3 а , и сложим раздельно для статора и ротора. Тогда получим:



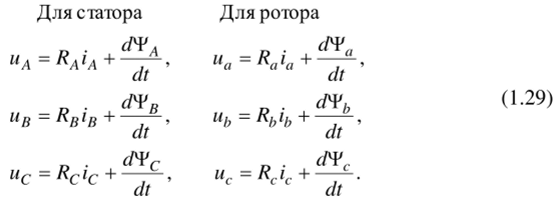
где L" L_r — собственные индуктивности статора и ротора; L_m(в) — взаимная индуктивность между статором и ротором.

Таким образом, вместо двенадцати уравнений (1.29, 1.30) получено лишь четыре уравнения (1.33).

Переменные коэффициенты взаимной индукции в уравнениях для потокосцеплений (1.33) являются результатом того, что уравнения равновесия эдс для статора записаны в неподвижной системе координат, связанной со статором, а уравнения равновесия эдс для ротора записаны во вращающейся системе координат, связанной с ротором. Метод пространственного вектора позволяет записать эти уравнения в единой системе координат, вращающейся с произвольной скоростью ы_к. В этом случае уравнения (1.33) преобразуются к виду:



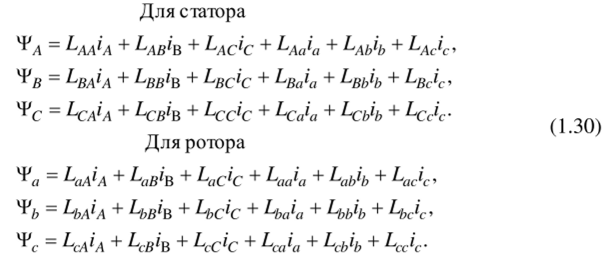
гдеco_m — частота вращения ротора; p — число пар полюсов в машине.

В уравнениях (1.34) все коэффициенты являются величинами постоянными, имеют четкий физический смысл и могут быть определены по паспортным данным двигателя, либо экспериментально.

Момент в уравнении (1.32) является векторным произведением любой пары векторов. Из уравнения (1.34) следует, что таких пар может быть шесть (is, iK); (Ts,^*); (is,'Vs); (is^r); (ir^s); (ir^s) — Часто в рассмотрение вводится иотокосцеиление взаимной индукции ЧЛи = L_m(is + /'/?). В этом случае появляется ещё четыре возможности представления электромагнитного момента машины через следующие пары: (is.'f'm); (г", Ч'_ш); ('Fs.'FmA (Ч-'я.Ч'ш). После выбора той или иной пары уравнение момента приобретает определенность, а количество уравнений в системе (1.34) сокращается до двух.



Кроме того, в уравнениях (1.31) и (1.32) векторные величины момента и скорости могут быть заменены их модульными значениями. Это является следствием того, что пространственные векторы токов и потокосцеплений расположены в плоскости, перпендикулярной оси вращения, а векторы момента и угловой скорости совпадают с осью. В качестве примера покажем запись уравнений момента через некоторые пары переменных состояния машины (1.35).

Приведём описание в относительных единицах.

На этом этапе уравнения (1.31), (1.34) и (1.35) приводятся к безразмерным (относительным) величинам [2]. В качестве основных базовых величин выбираются амплитудные номинальные значения фазного напряжения и тока, а также номинальное значение угловой частоты:

на этой основе определяются базовые значения всех переменных и коэффициентов, входящих в уравнения, а также базового времени:



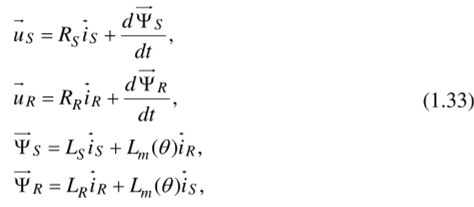
Обобщенная система уравнений для описания асинхронной машины принимает вид:



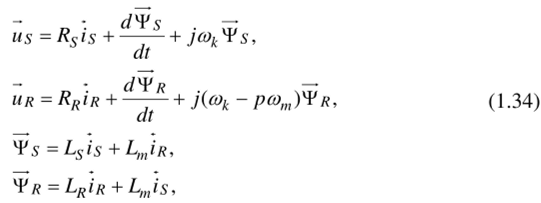
В этих уравнениях все переменные относительные, полученные как результат деления реальных значений на базовые, все коэффициенты также безразмерные, полученные аналогично.

Переменные и параметры в относительных единицах:

-и — / - Ф.

и =—, i=—, у/=— - относительные электромагнитные переменяй h %.

ные состояния;

ОЛ _ (О

а_к = —-, Э_т =-^ш- — относительная частота вращения системы коорди;

Щ, Щ>

нат и относительная частота вращения ротора;

М

т =—относительный момент на валу машины;

г =^, г = **-, _х = 3*3. _г x_R =^, Х_т=^, Т_т — относи;

я* /?" м"

тельные (безразмерные) параметры.

Расчет параметров асинхронной машины приведен ниже.

В уравнениях (1.38) время принято безразмерным t = — = co_ht, и.

h

единицей измерения времени является не секунда, a t_h = —. Следует.

(0_Ь

заметить, что введение относительных величин существенно сокращает время моделирования и позволяет устранить многие проблемы при моделировании.

Выводы:

• — существенное упрощение системы уравнений предлагает применение пространственного вектора;
• — применение системы координат (например, вращающейся с произвольной скоростью) позволяет избавиться от переменных коэффициентов при описании процессов в асинхронном двигателе;
• — использование безразмерной формы записи системы уравнений упрощает структуру уравнений и сокращает затраты времени на моделирование.