Цвет и его представления в компьютере

Одним из базовых терминов в компьютерной графике является цвет. Далее мы будем постоянно сталкиваться с ним, поэтому необходимо дать ему корректное определение. Несмотря на то что цвет является базовым понятием, интуитивно понятным каждому, строго определить его довольно сложно.

Есть несколько вариантов подхода к цвету, и наиболее очевидным из них является подход, основанный на физике. Как известно, свет — это поток электромагнитных волн. Попробуем дать определение цвета подобным образом.

Определим поток электромагнитных волн, содержащий волны различной длины X, с помощью плотности энергии (SPD, spectral power distribution) — функции 1(Х). Задав длину волны X и некоторую малую величину АХ, можно найти общую энергию, которая заключена в волнах с длинами от X до X + АХ, с помощью следующего интеграла: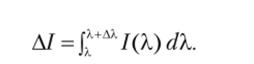

На рис. 3.1 приведена спектральная функция для дневного света, называемая Z)₆₅.

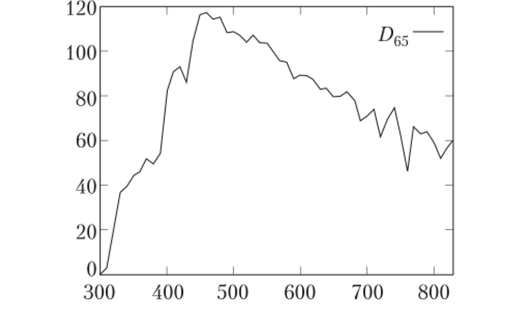
Рис. 3.1. Спектральная функция для дневного света.

Кажется, что мы можем сопоставить каждому цвету свою спектральную функцию 1(Х) и определять далее цвет с ее помощью. Такой подход обладает удобным свойством аддитивности: если мы хотим сложить два цвета (например, точка освещается двумя источниками разных цветов), то просто складываем соответствующие спектральные функции. Однако в действительности такой подход для представления цветов не работает. Одно и то же ощущение цвета (как его воспринимает человек) вызывается бесконечным количеством различных спектральных функций. Такие спектральные функции, вызывающие одно и то же ощущение цвета, называются метамерами. Подход, основанный на представлении цвета при помощи спектральной кривой, не подходит, поскольку мы даже не можем однозначно сопоставить каждому цвету единственную спектральную кривую.

Из этого следует, что для построения модели цвета мы должны опираться в первую очередь на то, как работает человеческий глаз. Можно представить глаз человека как оптический прибор, в котором есть свой аналог объектива — хрусталик — и светочувствительный элемент — сетчатка (рис. 3.2). С помощью глаза мы можем видеть не все электромагнитные волны, а только те, длина которых находится примерно в диапазоне 400—700 нм.

Рис. 3.2. Устройство человеческого глаза.

Хрусталик проектирует видимое изображение на сетчатку, покрытую светочувствительными клетками — палочками и колбочками. Палочки, расположенные в основном, но периферии сетчатки, обладают крайне высокой светочувствительностью, но при этом слабо различают длину волны. Именно палочки отвечают за так называемое ночное зрение и позволяют видеть при плохом освещении, но при этом мы не различаем цвета.

Если необходимо разглядеть что-то в темноте, то лучше не смотреть прямо на объект, а постараться увидеть его боковым зрением. При этом изображение попадет на периферию сетчатки, где находится большое количество палочек, обладающих высокой светочувствительностью.

Колбочки, расположенные в основном в центре сетчатки, обладают низкой светочувствительностью и узким диапазоном воспринимаемых длин волн. Именно за счет этих клеток мы различаем цвета, однако в силу их низкой светочувствительности мы плохо различаем цвета в темноте. Существуют три типа колбочек, чувствительных соответственно к коротким, средним и длинным волнам. Эти длины примерно соответствуют красному, зеленому и синему цветам. На рис. 3.3 приведены нормализованные чувствительности колбочек к волнам различных длин.

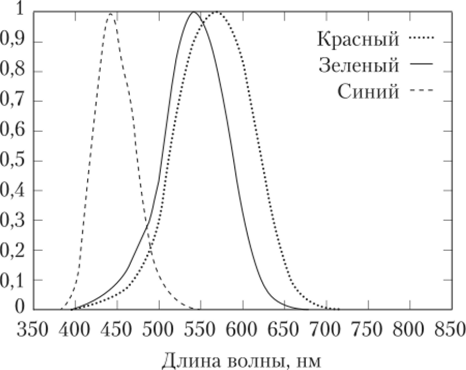
Рис. 33. Графики чувствительности колбочек к волнам различных длин Таким образом, мы приходим к следующему принципу: каждый цвет будем представлять как сумму трех базовых цветов — красного (Red, г), зеленого (Green, g) и синего (Blue, b) — с заданными весами. Именно эта тройка весов (г, g, b) и будет задавать цвет.

Соответствующая модель получила название RGB, и множество всех представимых цветов является единичным кубом (рис. 3.4). Таким образом, каждый цвет представляется как трехмерный вектор, компоненты которого определяют доли красного, зеленого и синего цветов, которые нужно смешать, чтобы получить заданный цвет.

В этой цветовой модели черный цвет представлен тройкой чисел (0, 0, 0), белый — тройкой (1, 1, 1), а диагональ куба, соединяющая соответствующие этим цветам вершины куба, соответствует оттенкам серого цвета.

Легко понять, что эта модель представления цвета также является аддитивной. При этом мы не определили сами базовые цвета: в зависимости от выбора этих базовых цветов будет меняться сам вектор, представляющий какой-либо конкретный цвет, т. е. эта модель должна быть привязанной к конкретным базовым цветам.

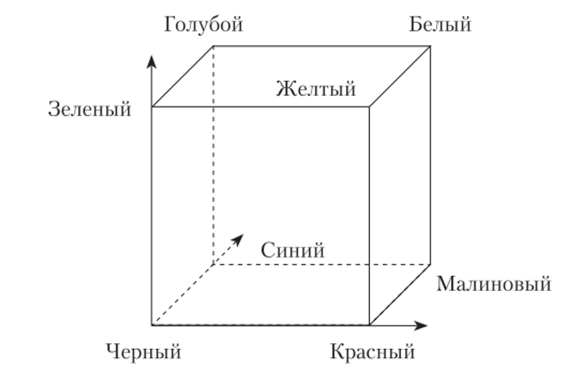
Рис. 3.4. Множество всех цветов для модели RGB.

Другим, гораздо более серьезным, недостатком модели RGB является следующий. В 1920;х гг. У. Д. Райт и Дж. Гилд провели серию опытов с привлечением групп наблюдателей. Задачей этих опытов было получение ЛСВ-представлений для большой группы цветов, в первую очередь чистых спектральных (т.е. состоящих из волн с одной и той же длиной волны) цветов.

В проводимых опытах наблюдателям показывали две точки: одна соответствовала разлагаемому цвету, а другая строилась как результат наложения точек от трех источников — красного, зеленого и синего цветов. Задачей наблюдателей было добиться идентичности цветов обеих точек путем изменения пропорций красного, зеленого и синего.

В результате этих опытов выяснилось, что далеко не все цвета можно представить в виде суммы красного, зеленого и синего. Более того, чистые спектральные цвета также нельзя представить таким образом. Однако при этом обнаружилось, что если к разлагаемому цвету прибавить определенный базовый цвет, то получившийся в результате цвет уже можно разложить на сумму базовых. Фактически это соответствует тому, что для представления некоторых цветов иногда получаются отрицательные веса.

Поскольку использование отрицательных весов крайне неудобно, в 1931 г. была создана модель CIE XYZ — стандарт представления цвета. В этой модели каждый видимый человеком цвет однозначно представлялся с помощью тройки неотрицательных чисел (X, У, Z), причем У-компонента соответствовала воспринимаемой человеком яркости.

На рис. 3.5 приведены весовые функции для определения цвета по его спектральной функции.

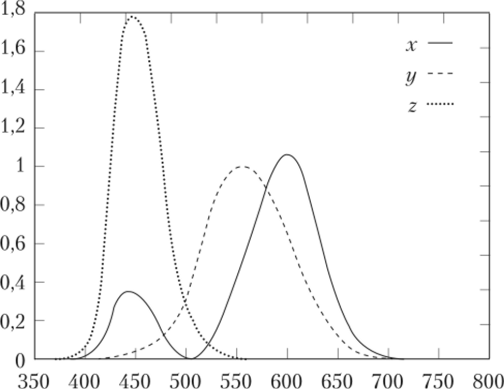
Рис. 35. Весовые функции для модели XYZ.

Для получения .XYZ-координат цвета по спектральной функции используют следующие формулы:

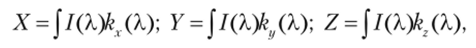
где k_x(k), k_y(X) и k₂()S) — определенные стандартом весовые функции.

Модель CIE XYZ является стандартом для представления цвета, и все остальные цветовые модели выражаются через нее. В частности, существует стандарт для телевидения высокой четкости (так называемый Rec 709), который явно задает используемые цвета (красный, зеленый и синий) их .XYZ-координатами:

В моделях CIE XYZ и RGB информация о цвете «размазана» по всем трем компонентам. Соответственно, существуют цветовые модели, в которых имеет место явное деление координат на яркость и так называемые хроматические координаты, задающие цвет без учета яркости. Одной из таких моделей является Yxy, определяемая по следующим формулам:

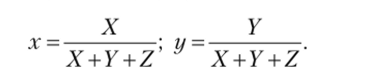
Хроматические координаты х и у полностью определяют цвет без учета его яркости. На рис. 3.6 приведена фигура (называемая хроматической диаграммой), которая содержит хроматические координаты всех видимых человеком цветов. На этом изображении дуга соответствует чистым спектральным цветам, а отрезок — цветам, получающимся при смешивании красного и синего цветов.

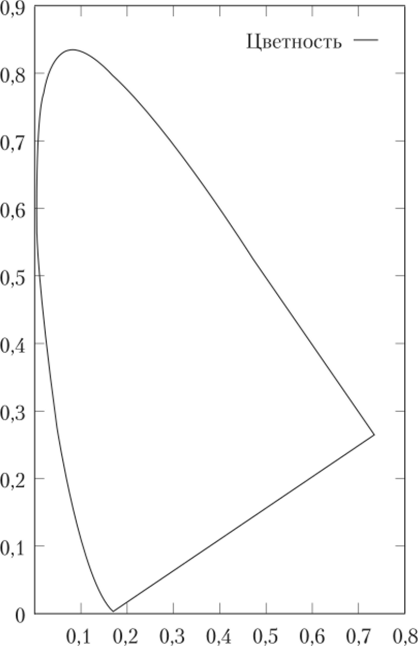
Рис. 3.6. Хроматическая диаграмма.

Если у нас есть два разных цвета, то им соответствуют две точки на хроматической диаграмме. Рассмотрим все множество цветов, которые получаются путем смешивания этих двух заданных цветов. Данному множеству будет соответствовать отрезок на хроматической диаграмме, причем концы этого отрезка соответствуют двум нашим цветам.

Аналогично, если у нас есть три цвета, то множество всех цветов, представимых при помощи их смешивания, будет являться треугольником на хроматической диаграмме, при этом вершины треугольника будут соответствовать этим трем базовым цветам.

Отсюда следует вывод — никакие три цвета (и вообще никакое конечное количество цветов) не могут дать при смешивании все видимые человеком цвета.

Несмотря на то что цветовое пространство CIE XYZ является стандартом, на практике почти для всех светоизлучающих устройств используют модель RGB, поскольку она проста и удобна. Хотя эта модель не может дать все видимые человеком цвета, ее, как правило, бывает достаточно. Глядя на экран монитора, человек обычно не замечает, что далеко не все цвета могут быть отображены на нем. Однако при печати цветных изображений обычно применяют совсем другую модель цвета. Рассмотрим, почему это происходит.

При цветной печати на поверхность белой бумаги наносятся слои красителей, каждый из которых отражает волны определенной длины, а остальные волны — поглощает. Например, когда мы видим красную точку на листе бумаги, это означает, что все волны, кроме соответствующих красному цвету, были поглощены. Поэтому нанесение цветного красителя на поверхность бумаги удобнее рассматривать как операцию вычитания какого-то цвета из белого цвета бумаги. Подобные цветовые модели обычно называются субтрактивными.

Как и в RGB-модели, здесь достаточно всего трех красителей для получения различных цветов. При этом в качестве базовых цветов (т.е. цветов красителей) используют цвета, получаемые при вычитании красного, зеленого и синего из белого цвета. Так, вычитая красный цвет (с координатами (1, 0, ())) из белого (имеющего координаты (1, 1, 1)), мы получаем цвет с RGB- представлением (0, 1, 1), т. е. голубой {Cyan). Аналогично, вычитая зеленый цвет из белого, получаем малиновый цвет (Magenta), а при вычитании синего из белого — желтый цвет {Yellow). При цветной печати обычно используют чернила этих трех цветов, и соответствующая цветовая модель получила название CMY. В этой модели каждый цвет определяется количеством чернил, которое нужно нанести на белую бумагу для получения заданного цвета. Для перевода между моделями RGB и CMY служит следующая формула:

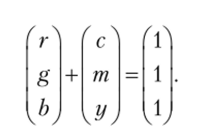
В этой цветовой модели белый цвет имеет координаты (0, 0, 0), а черный — (1,1,1). Оттенки серого цвета имеют вид (х, х, х).

Однако такое представление оттенков серого цвета имеет ряд недостатков. Прежде всего, цветные чернила довольно дорогостоящие. Кроме того, если мы хотим вывести точку черного цвета, то нам нужно наложить друг на друга три точки разных цветов. Если это наложение будет не очень точным, то вокруг черной точки мы увидим радужный край, что на практике очень заметно. Поэтому часто к трем базовым цветам модели CMY добавляют четвертый цвет — черный (ЫасК), получая модель, называемую CMYK. Ниже приведена формула для перевода из CMY в CMYK:

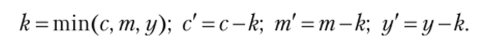
Кроме этих представлений (моделей) цвета, существуют и другие, более подходящие для каких-то определенных целей. Так, представление цвета в RGB (или CIE XYZ) удобно программистам, но художники часто представляют цвета другим образом — с помощью яркости (Value), насыщенности (Saturation) и тона (Hue). Такая цветовая модель называется HSV. При этом насыщенность цвета отражает, насколько данный цвет близок к серому цвету той же яркости, и меняется от 0 (серый цвет) до 1 (чистый цвет). Тон задает оттенок чистого цвета и является углом, изменяющимся от 0 до 360° (рис. 3.7).

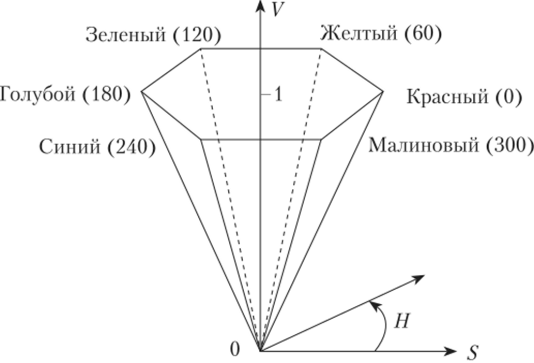
Рис. 3.7. Цветовое пространство HSV.

Таким образом, все множество допустимых цветов является перевернутой шестигранной пирамидой. Вершина этой пирамиды соответствует черному цвету (для него тон и насыщенность не определены), основание — цветам с наибольшей яркостью, боковые грани — чистым цветам различной яркости, высота — оттенкам серого цвета.

Ряд графических пакетов поддерживает работу с цветом в формате HSV. На рис. 3.8 приведен диалог выбора цвета из пакета Paint.net.

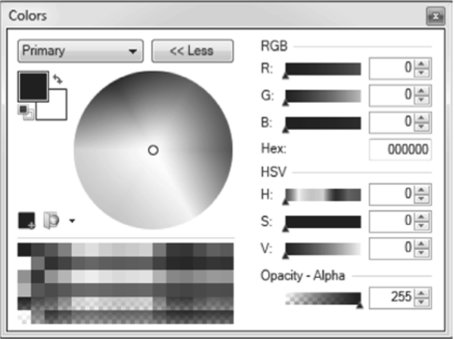
Рис. 3.8. Выбор цветов в пакете Paint.net.

Для преобразования из формата RGB в HSV используют следующие формулы:

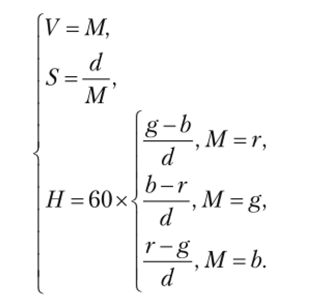
Используемая в модели HSV величина V не является воспринимаемой яркостью цвета, которая обычно представляет собой взвешенную сумму /?67?-компонент:

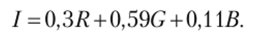
Здесь используются следующие величины:

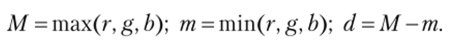
Помимо модели HSV еще существует модель HSL (Hue, Saturation, Lightness). Цветовое пространство, соответствующее этой модели, изображено на рис. 3.9.

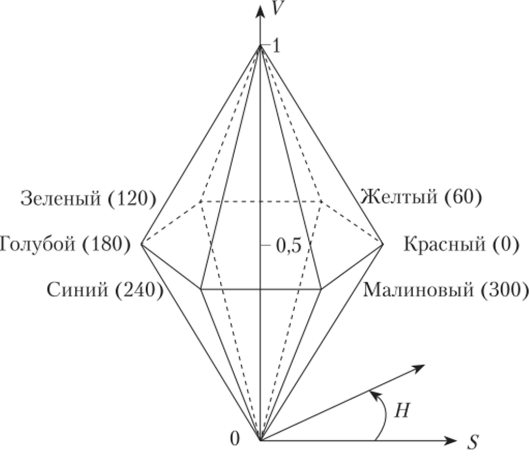
Рис. 3.9. Цветовое пространство HSL.

Для этой модели параметр L определяют по следующей формуле (все остальные параметры вычисляют так же, как и для HSV):

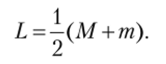
Так же, как и для модели HSV, величина L не является воспринимаемой яркостью цвета.

В рассмотренных моделях яркость — линейная функция от входного сигнала. Однако если мы рассмотрим основные графические устройства, такие как мониторы, то мы столкнемся с иной ситуацией. Между входным сигналом (например, подаваемым на вход напряжением) и выходным сигналом (яркостью) существует нелинейная зависимость, обычно записываемая в виде функции.

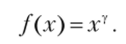
Соответственно, если мы хотим получить на экране вдвое большую яркость, то /?&В-компоненты цвета (т.е. входной сигнал, подаваемый на монитор) нужно увеличить не в два раза. Поэтому часто к вычисленному значению цвета применяют преобразование, обратное к хУ, для того чтобы компенсировать искажение, вносимое монитором. Этот процесс называется гамма-коррекцией.

Важным шагом в гамма-коррекции является определение истинного значения степени у для данного устройства. Для определения у на мониторах обычно прибегают к следующему способу: пользователю показывается два квадрата — один заполнен черными и белыми точками (обычно используется шаблон, как на шахматной доске), а второй заполнен точками одного и того же оттенка серого цвета. Пользователь может управлять яркостью серых точек, его задача — подобрать такую яркость, чтобы эти два квадрата имели одинаковую среднюю яркость. Для первого квадрата средняя яркость равна 0,5, для второго — хУ. Подбор яркости — это подбор такого х, что X* = 0,5. Найдя необходимое значение х, можно рассчитать и у.

Кроме такого способа, существуют и аппаратные способы определения у.

Контрольные вопросы и упражнения

• 1. Почему спектральные функции плохо подходят для представления цвета?
• 2. Что такое метамеры?
• 3. Какие цветовые модели вы знаете? Укажите различия между ними.
• 4. Напишите на языке C++ код для перевода цвета между CIE XYZ и Rec 709.
• 5. Напишите на C++ код для перевода цвета между RGB и CMY.
• 6. Напишите на C++ код для перевода цвета между RGB и CMYK.
• 7. Напишите на C++ функцию для перевода цвета между моделями RGB и HSV.
• 8. Напишите на C++ код для перевода цвета между RGB и HSL.
• 9. Объясните, исходя из хроматической диаграммы, почему нельзя представить все видимые человеком цвета с помощью взвешенной суммы трех цветов.
• 10. Напишите функцию, изменяющую яркость цвета, заданного в модели RGB, в k раз.
• 11. Напишите функцию, изменяющую насыщенность цвета, заданного в модели RGB, в k раз.
• 12. Напишите функцию, определяющую, является ли заданный в модели RGB цвет зеленым без учета яркости.