Бесконечные структуры данных

«Ленивость» конструкторов позволяет записывать и обрабатывать такие выражения, которые представляют собой потенциально бесконечные структуры данных. Элементов в такой структуре бесконечно много, но если в вычислениях требуется лишь конечное их число, то вычисление вполне может закончиться успешно, так как остальные «ненужные» элементы просто не будут никогда созданы. Такова, например, техника обработки потенциально бесконечных списков. В языке Haskell вполне корректным будет следующее определение бесконечного списка из единиц:

units: [Integer] units = liunits.

Это определение «зацикливается» самым примитивным образом, однако при ленивой схеме вычислений конструктор (:) не будет пытаться вычислять свои аргументы, так что элементы, расположенные после первой единицы, могут и не потребоваться. Конечно, если вы попробуете найти сумму всех элементов такого списка или обработать его иным способом, в котором потребуются все элементы списка, то программа зациклится в безнадежной попытке вычислить все единицы в этом списке. Однако функция, которая суммирует лишь первые несколько элементов, вполне может быть применена к такому «бесконечному» списку. Действительно, пусть имеется следующая функция, вычисляющая сумму первых п элементов числового списка:

summa:: Num, а => Int -> [а] -> а summa 0 _ = О.

summa n (x:list) = х + summa (n-1) list.

Попробуем теперь вычислить значение summa 3 units, учитывая, что вычисления в Haskell — ленивые. Мы получим следующую цепочку преобразований:

summa 3 units.

Здесь для вычисления результата нужно произвести сопоставление с образцом. Первое уравнение, очевидно, не подходит, а во втором для успешного сопоставления следует произвести подстановку определяющего выражения для units: summa 3 (lrunits).

Теперь сопоставление с образцом может быть произведено, х получает значение 1, a list — значение нашего бесконечного списка units. Используем второе уравнение:

1 + summa (3−1) units.

Функция арифметического сложения строгая, так что для получения окончательного значения ее второй аргумент необходимо вычислить. При новом сопоставлении с образцом первый аргумент функции summa — выражение (3−1) — также будет вычислен. Продолжим цепочку преобразований без комментариев:

• 1 + (1 + summa (2−1) units)
• 1 + (1 + (1 + summa (1−1) units))

Теперь уже при сопоставлении с первым образцом в определении функции summa будет выбрано первое уравнение, и мы получим выражение 1 + (1 + (1 + 0)).

которое будет успешно редуцировано до окончательного значения 3.

Итак, оказалось, что работа с бесконечным списком окончилась вполне успешно. Это произошло потому, что на самом деле нам не потребовался бесконечный список; после вычисления первых трех элементов остальные нс понадобились. Подобная техника может применяться в Haskell всегда, когда это удобно. Следующая функция выдает в качестве результата бесконечный список последовательных целых значений, начинающийся с заданного значения:

fromlnt: Integer -> [Integer] fromlnt n = n: fromlnt (n+1).

Теперь вызов этой функции fromlnt 1 дает в результате весь натуральный ряд. Однако запрашивать поиск последнего элемента в этом списке бесполезно; соответствующая программа просто зациклится. Вообще, бесконечную арифметическую прогрессию, подобную только что полученной, можно получить в Haskell еще проще, используя обычное синтаксическое обозначение для арифметической прогрессии [1.. ]. От конечной прогрессии это обозначение отличается тем, что верхняя граница прогрессии не указана. Бесконечные списки можно использовать везде, где можно применять и обычные конечные списки, до тех пор, пока не потребуется вычисление всех его элементов. Вот как, например, получить сумму первых 10 квадратов натуральных чисел с использованием нашей функции summa: summa 10 [х*х | х <- [1.]].

Нетрудно получить и более сложные списки, чем список квадратов. Например, ранее мы строили множество простых чисел, не превышающих заданного значения с помощью алгоритма решета Эратосфена. Функция получилась не очень простой, однако оказывается, что при работе с бесконечными списками тот же самый алгоритм можно реализовать значительно проще, чем представляя множество чисел характеристической функцией. Основой для реализации этого алгоритма может послужить конструкция, выкидывающая из списка s все числа, кратные заданному числу п: [х | х <- s, х 'mod⁴ п /= 0]. Тогда алгоритм решета Эратосфена может быть выражен с помощью рекурсивной функции просеивания sieve: sieve: [Integer] -> [Integer].

sieve (n:s) = n: sieve [x | x <- s, x 'mod' n /= 0].

Функция просеивания берет первый элемент некоторого, вообще говоря, бесконечного списка, и выкидывает из хвоста этого списка все элементы, делящиеся на первый элемент. После этого к результату фильтрации снова применяется функция просеивания, а первый элемент вновь присоединяется к результату этого просеивания.

Теперь список всех простых чисел получается применением функции просеивания к бесконечному списку чисел, начиная с двойки: primes = sieve [2.. ]. Отметим, что функция работает достаточно эффективно, последовательно удаляя из списка всех натуральных чисел те из них, которые делятся хотя бы на одно из уже полученных простых чисел.

Помимо бесконечной арифметической прогрессии имеется еще довольно много стандартных функций, с помощью которых можно построить бесконечные списки из конечных списков или отдельных значений. Приведем некоторые из них.

Функция repeat строит бесконечный список, содержащий один и тот же элемент в бесконечном числе экземпляров. Например, выражение (repeat 1) задает бесконечный список из единиц: (1: (1: (1:…))) > такой же, какой мы строили раньше с помощью функции units и какой может быть также определен с помощью бесконечной арифметической прогрессии с нулевой разностью [1,1.. ].

Функция cycle строит бесконечный список, повторяя бесконечно один и тот же фрагмент, заданный конечным списком — аргументом функции. Например, выражение (cycle [1.. 3]) задает бесконечный список [1,2,3,1,2,3,1,2,.. .].

Функция высшего порядка iterate строит бесконечный список из начального элемента, последовательно применяя заданную функцию к элементам строящегося списка. Каждый следующий элемент списка получается применением этой функции к предыдущему. Например, бесконечную геометрическую прогрессию со знаменателем 2 можно построить с помощью применения функции iterate следующим образом: iterate (*2) 1.

Еще один простой, но интересный пример — это получение списка, представляющего собой последовательность чисел Фибоначчи. Если мы уже имеем последовательность чисел Фибоначчи в виде бесконечного списка (обозначим его fib), то прежде всего образуем еще один бесконечный список, fib0, приписав ноль к началу последовательности чисел Фибоначчи: fibO = (0: fib). Теперь заметим, что если сложить почленно две наши последовательности fib и fibO, то в результате опять получится последовательность чисел Фибоначчи, только без первого члена. Операция почленного сложения списков может быть реализована с помощью стандартной функции над списками zipWith. Функция почленного сложения двух списков — это просто zipWith (+). Теперь последовательность чисел Фибоначчи можно будет сформировать с помощью следующей несложной конструкции:

fib = 1: zipWith (+) fib (0: fib).

Эту строчку можно прочитать так: «последовательность чисел Фибоначчи получается, если приписать единицу к результату почленного сложения самой этой последовательности и той же последовательности, к которой приписан в начале нулевой элемент». Данное определение рекурсивно определяет последовательность Фибоначчи и действительно порождает бесконечный список чисел Фибоначчи, но, конечно, только благодаря ленивым вычислениям в программах на языке Haskell.

Стоит упомянуть еще одну интересную технику написания программ для работы с бесконечными списками. В этой технике, называемой завязыванием узлов, программа сначала представляется в виде схемы, на которой бесконечные списки представлены в виде потоков и изображаются на схеме стрелочками. Например, упомянутая выше последовательность чисел Фибоначчи будет представлена в виде потока, изображенного на рис. 7.1.

Рис. 7.1. Изображение потока.

Потоки могут обрабатываться почленно функциями, подобными показанной выше функции zipWith (+), при этом из одного или нескольких потоков образуется новый поток. Например, если потоки нужно почленно складывать, то на схеме изображается элемент, выполняющий сложение, в виде прямоугольника, содержащего обозначение операции сложения. Потоки-операнды входят в этот прямоугольник, а поток-результат — выходит из нее. Часть схемы, содержащая такую обработку, будет выглядеть так, как показано на рис. 7.2.

Рис. 7.2. Сложение потоков

Наконец, если к потоку нужно приписать дополнительный первый элемент (это соответствует применению конструктора списков (:)), то на схеме рисуют треугольник, входами в который являются поток и добавляемый в него элемент, а выходом будет результирующий поток с добавленным первым элементом. Например, приписывание нуля к потоку, изображающему последовательность чисел Фибоначчи, на схеме будет выглядеть так, как показано на рис. 7.3.

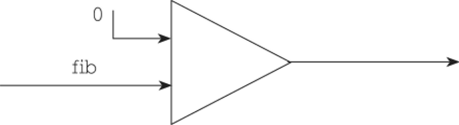
Рис. 73. Приписывание элемента к потоку

Описанное выше взаимодействие потоков, в результате которого получается последовательность чисел Фибоначчи, можно теперь изобразить в виде схемы, показанной на рис. 7.4.

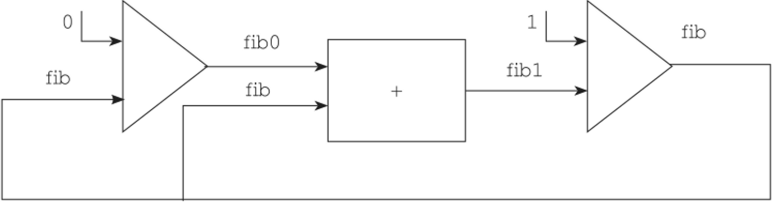
Рис. 7.4. Схема потоков для вычисления последовательности чисел Фибоначчи.

Теперь программу на языке Haskell, реализующую изображенную схему взаимодействия потоков, можно получить автоматически. Для этого нужно просто описать все узлы данной схемы в виде серии взаимно-рекурсивных определений. В этих определениях каждый поток получается как результат применения функций к другим потокам и отдельным значениям. Например, поток, выдающий последовательность чисел Фибоначчи, описывается следующим выражением, которое в точности следует нарисованной схеме: fibonacci = let fibO = 0: fib.

fibl = zipWith (+) fibO fib fib = 1: fib 1 in fib.