Формулы Гаусса — Кристоффеля

В этом параграфе мы рассмотрим вычисление интегралов специального вида.

где р (х) называется весовой функцией. До сих пор в этой главе мы имели дело с квадратурными формулами, в которых подынтегральная функция вычислялась в заданных точках (узлах). Теперь мы обсудим некоторые специальные формулы для интеграла (5.13), которые имеют следующий вид (формулы Гаусса — Кристоффеля):

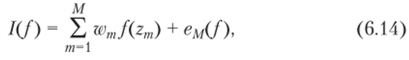
где веса W,…, w_M и узлы z_t, …, z_M — свободные параметры. Следует заметить, что весовая функция р (х) не участвует в вычислениях явным образом. Как мы увидим позднее, она влияет на выбор весов и узлов в формуле (6.14). Наша цель состоит в определении этих параметров таким образом, чтобы квадратурная формула (6.14) имела наименьшую возможную погрешность. Так как теперь мы имеем 2 М параметров w_m и z_m то можем построить формулу, которая дает точное значение интеграла (&м (/) = 0) от всех полиномов степени не выше чем 2М — 1. Поясним это утверждение на примере. Пусть функция /(х) есть полином третьей степени: f (x) = а₃х³ + а₂х² +р_{х + р₀ и [с, d = [0, 1]. Пусть также р (х) = 1 и М = 2. Предположим, что квадратурная (формула.

(6.14) дает точное значение интеграла (6.13). Тогда мы имеем.

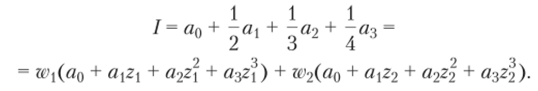
Перепишем это выражение в виде.

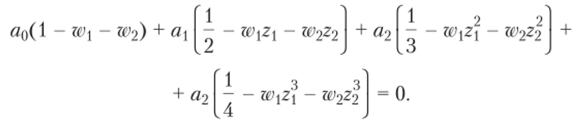
Решение системы уравнений.

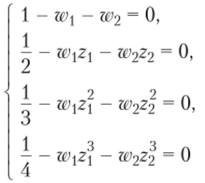
дает веса w, w₂ и узлы z_h z₂ квадратурной формулы, которая точна для полиномов третьей степени.

Возвратимся теперь к интегралу (6.13). Если.

• 1) р (дг) > 0 на интервале [с, d] и р (х) g С⁽⁰⁾[с, d]; d
• 2) fp (x)dx существует,

с

тогда существует набор полиномов Р_п(х)_у ортогональных на отрезке [с, d] с весовой функцией р (х), т. е.

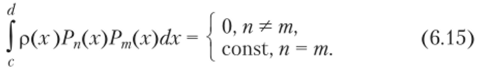
Все нули этих полиномов вещественны и расположены внутри отрезка [с, d]. Составим полином степени М по узлам квадратурной формулы:

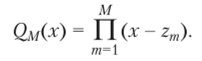
Пусть f (x) = Q (x)P_m(x) и если т< М — 1, то функция /(х) есть полином степени не выше 2М — 1. Следовательно, формула (6.14) точна для этой функции. Это даст.

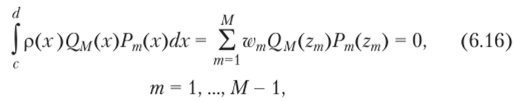
так как Qm (z,") ⁼ 0- Значит, полином Qm (x) ортогонален ко всем полиномам Р_т(х) степени т < М — 1. Разложим теперь Ом (х) по полиномам Р_п(х):

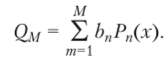
Подставим это выражение в (6.16) и, учитывая (6.15), получим.

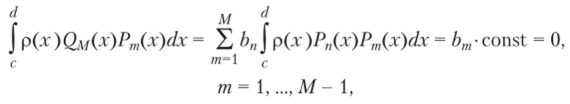
т.е. Ь_т = 0 когда т < М — 1. Тогда согласно нашему разложению Qm (x) совпадает с P (x):

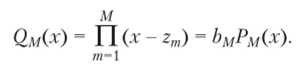
Следовательно, узлы квадратурной формулы (нули полинома Qm (x)) являются нулями Р_м(х). Получим выражение для весов квадратурной формулы. Составим полином.

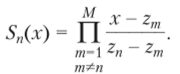
Это полином степени М — 1, и формула (6.14) для него точна. Учитывая, что S"(z_m) ^ 0 когда т = п, получим.

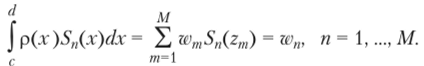
Для некоторых интегралов вида (6.13) узлы и веса квадратурной формулы (6.14) известны, например, для следующих случаев, часто встречающихся на практике:

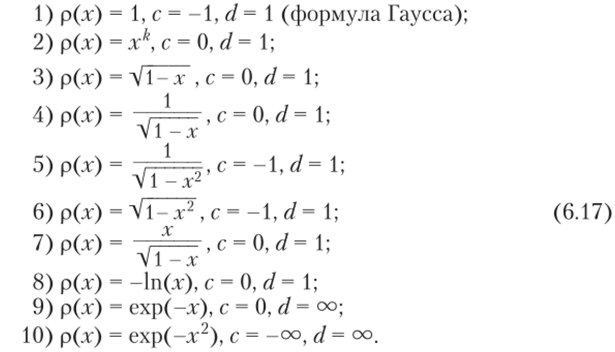
Выражение для ошибки квадратурных формул (6.14) можно представить в виде.

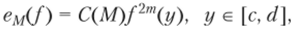
и они являются наиболее точными формулами для вычисления интегралов от гладких функций. Более подробную информацию о вычислении интеграла (6.13) с весовыми функциями (6.17) можно найти в Приложении, А Это приложение включает в себя информацию о соответствующих ортогональных полиномах, табличные данные о весах и узлах квадратурных формул, а также значения констант ошибки С (М).

Контроль ошибки формул Гаусса — Кристоффеля осуществляется путем выбора подходящего количества узлов интегрирования (чем больше узлов, тем меньше константа С (М)). Когда р (х) = 1, квадратура Гаусса может быть применена к интегралу по конечному отрезку а, Ь (с помощью преобразования х = (Ь + а)/2 + z (h — а)/2):

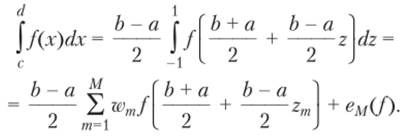
В этом случае используется смешанный подход к контролю ошибки. Если мы разделим интервал интегрирования [а, /;] на отрезки длиной /г, то можно построить следующую формулу интегрирования:

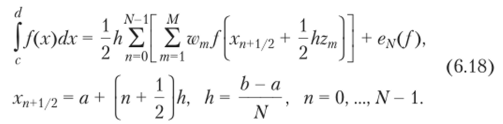
Выражение для ошибки этой формулы имеет вид.

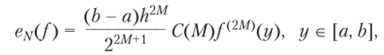
и теперь ошибка зависит не только от числа узлов в каждом подинтервале [х_п, х_и+1], но и от шага h.

Пример 6.3 (формула Гаусса) Рассмотрим интеграл из примера 6.1:

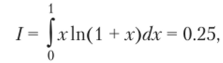
где подынтегральная функция f (x) е 1]. Используем квадратурную формулу (6.18) (N — 1, h — 1) с тремя узлами и весами (М = 3), и в данном случае она примет вид.

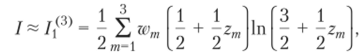
где w_m и z," равны (см. табл. А1 в Приложении А):

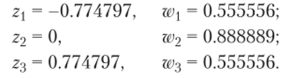
Вычисление дает следующий результат: 1 ~ 0.249 992 с абсолютной ошибкой е = 1−1 ~ 7.62 • 10 ⁶. Этот пример демонстрирует, что формула Гаусса позволяет вычислять интегралы с высокой точностью, даже если мы используем всего несколько узлов.