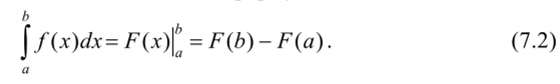Численное интегрирование. 
Информатика.

Ряд технологических задач требует увязки в математическое описание всей информации о процессе. Например, для математических моделей химико-технологических процессов одними из основных параметров, характеризующих процессы, являются концентрации реагирующих веществ, температура процесса и др. Как правило, большинство балансовых уравнений в химической технологии представлены системой интегральных и дифференциальных уравнений, в результате решения которых могут быть получены зависимости, характеризующие протекание процесса. Интегральные уравнения встречаются при описании гетерогенной кинетики, в теории активированного комплекса, при описании процессов в химических реакторах и т. д.

Часто на практике нс удастся вычислить интеграл аналитическим путем. В этих случаях применяют приближенные методы численного интегрирования.

Постановка задачи. Вычислить определенный интеграл.

при условии, что а и b конечны и F (x) является непрерывной функцией х на всем интервале хе[а, Ь. Во многих случаях, когда подынтегральная функция задана в аналитическом виде, интеграл от этой функции в пределах от а до Ь может быть вычислен по формуле Ньютона-Лейбница:

Однако этой формулой часто нельзя воспользоваться по следующим причинам:

• • первообразная функция Дх) слишком сложна и ее нельзя выразить в элементарных функциях;
• • функция Дх) задана в виде таблицы, что особенно часто встречается в задачах химической технологии при обработке экспериментальных данных.

В этих случаях используются методы численного интегрирования. Задача численного интегрирования состоит в нахождении приближенного значения интеграла (7.1) по заданным или вычисленным значениям.

Общий подход к решению задачи будет следующим. Определенный интеграл представляет собой площадь, ограниченную кривой Дх;), осью х и переменными х = а и х = Ь. Необходимо вычислить интеграл, разбивая интервал [а, Ь на множество меньших интервалов, находя приблизительно площадь каждой полоски и суммируя их.

В зависимости от способа вычисления подынтегральной суммы существуют различные методы численного интегрирования (методы прямоугольников, трапеций, парабол, сплайнов и др.).