Исходные положения термодинамики

В результате обобщения опытов в классической термодинамике постулируется, что изолированная макроскопическая система с течением времени приходит в состояние термодинамического равновесия и никогда самопроизвольно выйти из него не может. Это — первое (основное) исходное положение термодинамики. В статистической физике, где явно учитывается движение частиц, под термодинамическим равновесием подразумевается наиболее вероятное состояние, которое чаще всего создается непрерывно движущимися частицами и в которое переходит изолированная система с течением времени. Отсюда следует, что классическая термодинамика не рассматривает системы, для которых равновесное состояние невозможно и в которых наблюдаются большие самопроизвольные отклонения системы от равновесного состояния. Отмечено, что самопроизвольные отклонения термодинамической системы от равновесия при прочих равных условиях тем меньше, чем больше частиц в системе.

Опыты показывают и то, что если две равновесные системы, А и В привести в тепловой контакт, то, независимо от различия или равенства у них внешних параметров, они или остаются по-прежнему в состоянии термодинамического равновесия, или равновесие в них нарушается и через некоторое время в процессе обмена энергией обе системы приходят в другое равновесное состояние. Отсюда следует, что состояние термодинамического равновесия системы зависит не только от ее внешних параметров а;, но и еще от одной величины Т, характеризующей ее внутреннее состояние. Ога гипотеза подтверждается и тем, что если имеются три равновесные системы А,.

B, С и если системы, А и В порознь находятся в равновесии с системой.

C, то системы, А и В находятся в термодинамическом равновесии и между собой (свойство транзитивности термодинамического равновесия). Последнее свойство позволяет сравнивать значение величины Т у разных систем, нс приводя их в непосредственный тепловой контакт между собой, а используя другое тело. Величина Т, имеющая одно и то же значение у всех частей равновесной системы независимо от ее массы и определяемая внешними параметрами и энергией, характеризует состояние внутреннего движения системы и называется температурой. Температура является интенсивным параметром и служит мерой интенсивности теплового движения частиц системы. Существование температуры как особой функции состояния равновесной системы представляет второе исходное положение термодинамики.

Второе исходное положение термодинамики можно сформулировать и по-другому. Ранее было показано, что равновесное состояние термодинамической системы характеризуется внешними и внутренними параметрами, причем последние зависят от положения и движения частиц системы и значений внешних параметров. Согласно же второму постулату, состояние термодинамического равновесия определяется совокупностью внешних параметров и температурой. Следовательно, внутренние параметры хотя и характеризуют состояние системы, но не являются ее независимыми параметрами. Таким образом, все равновесные внутренние параметры системы являются функциями внешних параметров и температуры (еще одно определение второго исходного положения). Если мы выразим температуру системы через ее энергию, то получим, что при термодинамическом равновесии все внутренние параметры системы являются функциями внешних параметров и энергии.

№ второго исходного положения термодинамики следует существование уравнений состояния системы, связывающих температуру Т, внешние параметры а, и какой-либо равновесный внутренний параметр tv.

Если в качестве bt взять внутреннюю энергию 1), то уравнение.

называется калорическим уравнением состояния. С помощью уравнения (2.2.2) вычисляются теплоемкости и другие аналогичные величины. Уравнение (2.2.2) позволяет определить внутреннюю энергию U (ai, …, Эп; Т) в состоянии (ai…а"; Т) только с точностью до аддитивной постоянной, зависящей от выбора начального состояния.

Если вместо К взять сопряженную внешнему параметру а; обобщенную силу А;, то уравнения.

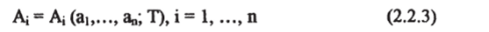
называются термическими уравнениями состояния, с их помощью определяется температура Уравнения (2.2.2) и (2.2.3) не являются независимыми, они связаны дифференциальным уравнением в частных производных. Общее число термических и калорического уравнений состояния системы равно числу независимых параметров, характеризующих состояние системы. Это число обычно называется числом степеней свободы.

Если уравнения (2.2.2) и (2.2.3) известны, то с помощью начал термодинамики можно определить все термодинамические свойства системы. Сами же уравнения состояния на основе термодинамики вывести нельзя. Оки находятся эмпирическим путем или методами статистической физики.