Численный метод расчета статически определимых стержней при изгибе

Описание численного метода начнем с решения уравнения второго порядка. Перепишем дифференциальное уравнение (7.5) в форме системы двух дифференциальных уравнений первого порядка, разрешенной относительно первых производных. Такая запись называется формой Коши и является удобной для перехода к векторно-матричной форме записи:

В векторно-матричной форме система будет выглядеть следующим образом:

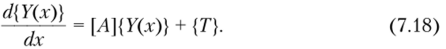
Здесь {У} — вектор-столбец неизвестных функций; [Л] — матрица коэффициентов в дифференциальных уравнениях; {Т} — вектор-столбец свободных членов, или вектор нагрузок:

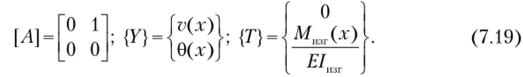
Однородная система уравнений, соответствующая системе (7.18), характеризуется нулевым вектором-столбцом свободных членов и имеет вид.

Система (7.18) интегрируется совместно с дополнительными условиями, количество которых соответствует порядку системы. В случае задания дополнительных условий на границе они называются граничными условиями.

В случае если все дополнительные условия заданы в начальной точке интегрирования, т. е. полностью известен начальный вектор (У (0)} = {У₀}, решение системы (7.18) сводится к начальной задаче, известной как задача Коши. Решение задачи Коши находится посредством однократного численного интегрирования системы (7.18). Интегрирование проводится с использованием одного из известных методов, которые реализованы в виде программ для ЭВМ.

В случае если граничные условия заданы в разных точках интервала интегрирования, в частном случае — начальной и конечной точках, возникает краевая задача.

Общий метод решения краевой задачи заключается в нахождении недостающих компонент вектора {У₀}, называемых начальными параметрами, и сведении краевой задачи к задаче Коши.

Рассмотрим метод решения линейной краевой задачи, называемый методом начальных параметров. Решение линейного векторно-матричного уравнения (7.18) можно представить в виде суперпозиции общего и частного решений:

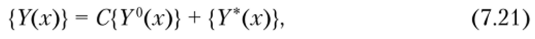
где С — подлежащая определению константа; (У°(.г)} — вектор-функция общего решения однородного уравнения (7.20); (У*(х)} — вектор-функция любого частного решения неоднородного уравнения (7.18). Получение этих решений производится численным интегрированием соответствующих векторно-матричных уравнений.

Рассмотрим изгиб шарнирно закрепленного по концам стержня (рис. 7.5). Задача является статически определимой, что предполагает возможность предварительного определения закона изменения изгибающего момента М_изг(х).

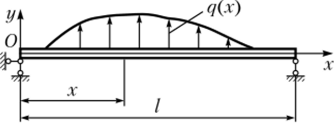
Рис. 75. Изгиб шарнирно закрепленного по концам стержня.

Из двух компонент начального вектора {У₀} известна только одна — перемещение в точке О. Если бы нам был задан угол поворота начального сечения, то проблема была бы сразу сведена к задаче Коши. Однако угол поворота заранее неизвестен, зато задано дополнительное условие на правом краю стержня. Краевые условия задачи запишутся в виде.

Суть алгоритма заключается в сведении решения краевой задачи к последовательному решению начальных задач. Сформируем начальные условия, выполняя следующие правила.

• 1. При формировании начальных векторов для общего решения в позиции заданных компонентов непосредственно ставятся их известные значения.
• 2. Во все позиции неизвестных компонентов поочередно ставится единица, при этом остальные позиции неизвестных компонентов заполняются нулями.
• 3. Поскольку в качестве частного решения неоднородного уравнения может использоваться любое решение, для его нахождения используется нулевой начальный вектор.

Для рассматриваемой задачи достаточно сформировать только два начальных вектора для нахождения общего и частного решений соответственно, которые запишутся в следующем виде:

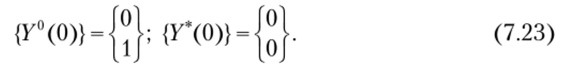
Поскольку перемещение в начальной точке известно (г;(0) = 0), в первой строке начального вектора для нахождения общего решения {F°(0)} поставлен нуль. Угол поворота в начальной точке неизвестен, поэтому во второй строке вектора поставлена единица. Начальный вектор для нахождения частного решения принят нулевым. При таком формировании начальных векторов граничное условие при х = 0 (7.22) удовлетворяется тождественно:

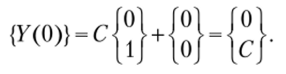
Отметим, что при представлении начальных векторов в такой форме постоянная С имеет смысл угла поворота начального сечения и подлежит определению. Для установления значения постоянной С рассмотрим значение вектора-решения на другом конце стержня, полученное в результате двукратного интегрировании уравнений (7.18) и (7.20) с начальными векторами (7.23) соответственно:

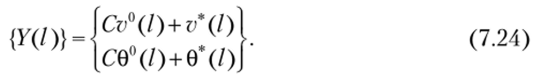
Согласно граничному условию на правом конце Cv°(l) + v*(l) = 0, откуда находим.

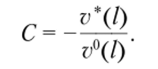
После нахождения С проводится чистовое интегрирование с начальным вектором.

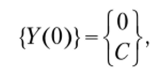
позволяющее определить вектор {У (х)} ^в любом сечении стержня.

Аналогично рассматриваются и другие виды опор однопролетного стержня в случаях его статической определимости.