Использование субъективных вероятностей при отсутствии знаний о физических вероятностях

Рассматривается подход, отличающийся от описанного использованием субъективных вероятностей в условиях отсутствия знания объективных вероятностей. В работах L.J. Savage^[1] была построена теория выбора при неопределенности, где существование субъективных вероятностей и форма критерия выбора выводятся непосредственно из аксиом предпочтения. Такой подход позволяет строить теорию без обращения к теории принятия решений в условиях риска и понятию физических вероятностей.

Обратимся к проблеме правдоподобия суждений. Для иллюстрации рассмотрим ситуацию, когда в некотором состязании участвуют три команды — А, В и С, и существует некоторый эксперт, отвечающий на вопросы о том, что правдоподобнее из возможных событий. Например, что в чемпионате победит команда А или команда В. Или вопросы более сложной формы, например, такой вопрос: что правдоподобнее — С займет место выше А или А выше В. Нужно отметить, что букмекерские конторы принимают ставки и на такие события; при том ясно, что выигрыш прямо зависит от правдоподобности или вероятности того или иного события. Букмекер как раз и должен быть своего рода экспертом, который определяет эти вероятности.

Изучаемая здесь проблема заключается в том, чтобы по совокупности суждений о сравнительной вероятности для пар событий установить, являются ли эти представления состоятельными в том смысле, чтобы можно было математически правильно задать вероятности всех событий. При этом, конечно, эти субъективные вероятности должны соответствовать представлениям о сравнительной вероятности рассматриваемых событий.

Таким образом, проблема сводится к тому, чтобы с каждым событием связать число (вероятность) так, чтобы величина этого числа соответствовала представлению о вероятности наступления события.

Очевидно, что это не всегда можно сделать. Например, если победа команды А представляется более вероятной, чем победа команды В, победа команды В — более вероятной, чем победа команды С, а победа команды С — более вероятной, чем победа команды А, поставленная задача становится неразрешимой. Несложно заметить, что в данном примере происходит нарушение свойства транзитивности и что рассматриваемая проблема связана с проблемой исчислимости предпочтений. Однако сама по себе задача отыскания вероятностей более сложна. Здесь речь идет о сопоставлении числовых оценок всевозможным подмножествам некоторого множества, причем сама функция вероятности должна отвечать определенным свойствам (аксиомам вероятности).

Напомним содержание аксиоматики А. Н. Колмогорова, составляющей основу математического описания теории вероятностей.

Пусть Q — множество элементарных событий, Q = {сор …, со_/;}, где co_i — элементарное событие, i = 1, п. Множество ft подмножеств Q. (называемых случайными событиями) называется а-алгеброй, если удовлетворяет следующим аксиомам:

• 1) Q g g;
• 2) если А е ft, то А е ft;

оо.

3) если Л_р …, А_п,… е ft, то U A_i е ft.

i= 1.

Вещественная функция Р, определенная на ft, называется вероятностью, если удовлетворяет следующим аксиомам:

• 4) Р (А) > 0 для любого /left;
• 5) P (Q) = 1;

/ оо оо.

• 6) если Лр …, Л_и,… g ft и А. П Л, = 0 при г ^ j, то Р U A_i = X Р (Л_У).
• 0=1 ) 1−1

Обратите внимание!

Вероятность является счетно-аддитивной мерой, определенной на а-алгебре случайных событий. Свойства (1)—(6) составляют систему аксиом теории вероятностей, составленную А. Н. Колмогоровым в 1929—1933 гг.

Введем, как и в предыдущем параграфе, множество S = {s_v …, s_n,…} состояний природы (сценариев). Подмножества множества 5 обозначим 5, и будем называть их событиями. Введем отношение сравнительной вероятности >_р на событиях: утверждение «Событие 5, не менее вероятно, чем событие 5*2» будем записывать как S_x >_р 5₂. Будем считать, что отношение задано на всех событиях. Считая полным упорядочением, свяжем с отношения строгого предпочтения >_р и безразличия обычным образом. Ранее эта связь более подробно изучалась в параграфе 14.2, в данном случае все соотношения абсолютно аналогичны.

Следующая теорема устанавливает условия, при которых существуют согласованные с >_р субъективные вероятности событий. Это означает, что для каждого события 5, — может быть определено единственное число <7(5,) € [0, 1], такое, что выполнены следующие условия:

a) (5, >, Sj) " (q (S,) > q (Sj)) при i *j;

b) q (S) = 1;

c) для непересекающихся событий 5, и S_f (5, П 5_; = 0 при i ^ j)

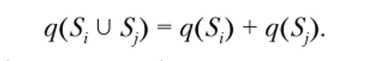
Рассмотрим подробно вопрос об отличии описанной выше системы условий от аксиоматики Колмогорова. Если для всех событий заданы q, отвечающие условию ©, то говорят, что на событиях 5 задана конечно-аддитивная мера q.

Обратите внимание!

Для того чтобы конечно-аддитивная мера q была вероятностной мерой (вероятностью), нужно, чтобы помимо выполнения условия Ь) условие с) выполнялось не только для конечных, но и для счетных наборов событий (условие счетной аддитивности).

При этом, как было упомянуто раньше, в соответствии с аксиоматикой Колмогорова, вероятность определяется на а-алгебре множеств так, чтобы выполнялось условие счетной аддитивности.

Теорема Сэвиджа о субъективной вероятности Пусть отношение ?,_р удовлетворяет следующим условиям. Для любых 5;, S_Jt 5* € 5 (i * k)

• 1) 5₍^0 для любого i;
• 2) >_p — слабое упорядочение;
• 3) ((5, u Sj) n 5; = 0) => ((5, >, Sj) «((5, U S_k) >_p (Sj U S_km
• 4) если 5, }Z_P S_r то существует конечное разбиение R множества 5, такое, что для любого R е R выполнено 5, }Z_P (5_у U R).

Тогда существует единственная согласованная с ^_р система субъективных вероятностей q. При этом для любого события 5, и любого числа, а е [0, 1] можно указать событие 5, такое, что <7(5,) = сс.

Доказательство данной теоремы представлено в ряде работ L. J. Savage^[2] и Р. С. Fishburn^[3]. Сейчас обратим внимание на подробное изучение содержания описанной выше теоремы.

Условие 1) очевидным образом утверждает, что вероятен хотя бы один сценарий множества S. Условие 2) является констатацией того, что любое событие, являющееся подмножеством S, не менее вероятно, чем пустое множество, т. е. наделено неотрицательной вероятностью. В условии 3) отмечается, что отношение >_р является отношением слабого упорядочения. Этот факт легко устанавить исходя из определения >_р с учетом его связи с отношением ^_р, а также проверки свойств асимметрии и отрицательной транзитивности, присущих отношению слабого порядка (ранее оно упоминалось в параграфе 14.2 и было подробно изучено в главе, посвященной моделированию предпочтений).

Условие 4) говорит о том, что если событие 5, кажется более вероятным, чем Sj, то событие (5, или S_k) должно казаться более вероятным, чем (Sj или S_k) для любого S_k} не пересекающегося с S_} и S_f. По сути, это условие является основным и обеспечивает аддитивность вероятности.

В условии 5), по аналогии с условием 4), говорится о том, что объединение менееили равновероятного события с любыми подмножествами множества S сохраняет его соотношение с изначально не менее вероятным событием.

Вывод теоремы говорит о бесконечности множества S. Более того, мера q не должна быть зависимой от структуры счетного множества {s_v …, s_n,…} с S. Это является следствием условия 5) теоремы.

Например, предположим, что q приписывает состояниям {5,…, s_w,…} ве- 111 1.

роятности …, —,… Тогда имеет место отношение s₃ >_р s₄. Для выполнения условия 5) необходимо разбить множество S на события, мера каждого из которых была бы меньше 1/16, что невозможно. Легко видеть, что такое же рассуждение справедливо для других s_{. Таким образом, S должно быть не более чем счетным, а мера q — независимой от структуры множества {.V, …, S_ny …}.

Существуют определенные сложности в трактовке q как вероятностной меры, поскольку в соответствии с теоремой мера q не является счетно-аддитивной.

В работе С. Villegas^[4] было указано, что мера q становится вероятностью, если дополнить условия, предложенные Сэвиджем, условием монотонной непрерывности: для любых S_x <= S₂ <= … и S = (JSj

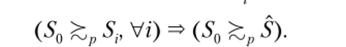
Однако в этом случае q уже не может быть определена на всех подмножествах S.

Подытожим все выше сказанное. В задачах принятия решений в условиях неопределенности не всегда доступна информация о физических вероятностях основных событий. Более важную роль в данной проблематике играют субъективные вероятности или иногда некоторые назначенные ЛПР «веса». На основе аксиоматизации предпочтений учеными (Ауманн, Энскомб, Сэвидж и др.) с помощью различного математического инструментария было установлено существование субъективных вероятностей и критерия выбора в виде меры q, обладающей всеми основными свойствами вероятности, за исключением того, что она является не счетно-аддитивной, а конечно-аддитивной мерой.

• [1] Savage L.J. The Foundations of Statistics. New York: Wiley. Dover edition, 1972 (1954). 294 p.
• [2] Savage L.J. The Foundations of Statistics. New York: Wiley. Dover edition, 1972 (1954). 294 p.
• [3] Fushbum P. C. The Axioms of Subjective Probabily // Statistical Science. 1986. No. 3. Vol. 1.P. 335−358.
• [4] Villegas C. On Qualititivc Probavility a-Algebras // Annals of Mathematical Statistics. 35.1964. P. 1787−1796.