Матричное дифференциальное уравнение

Вы. конечно, многократно использовали формулу для умножения матриц: если матрица А = (йу) умножается на матрицу В = (6у) (мы здесь будем для простоты говорить о квадратных матрицах порядка п,

поэтому границы изменения индексов указывать не будем), то их произведение матрица С = (с^) вычислится, но формуле.

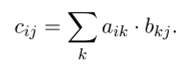
Эта формула имеет красивую геометрическую мнемонику: чтобы получить элемент г-й строки j-vo столбца матрицы С. надо перемножить г-ю строку матрицы А на j-Pt столбец матрицы В.

Попробуем разобраться в этом правиле поподробнее.

Чтобы получить сц, нам надо умножить первую строку матрицы А на первый столбец матрицы В. Чтобы получить С21 вторую строку матрицы А на … опять первый столбец матрицы В. Поучается интересная вещь: для получения элементов первою столбца матрицы С нам оказался необходим только первый столбец матрицы В Остальные столбцы ни при чем.

Такое замечательное свойство матричного умножения позволяет «развалить» одно матричное соотношение на набор векторных: первый столбец матрицы С (это вектор) равен произведению матрицы А на первый столбец матрицы В. второй столбец матрицы С равен произведению матрицы А на второй столбец матрицы В и так далее.

Возможно и обратное «собрать» из серии векторных соотношений с одной и той же матрицей одно матричное^[1]. Именно эта операция понадобится нам при построении матричного дифференциального уравнения. Мы ведь уже неоднократно сталкивались в наших выкладках с определителем Вронского определителем матрицы, составленной из векторов, каждый из которых является решением системы, и поэтому было бы грешно не подумать о том, какими же дифференциальными свойствами обладает сама матрица.

Весь предыдущий разговор велся, собственно, с единственной целью чтобы стало очевидно, что набор векторных тождеств.

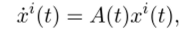
записанных для каждого решения системы, можно объединить в одно, если обозначить матрицу, составленную из векторов x^l(t). через X (t) (и тогда X (t) окажется матрицей из производных этих векторов). Результатом такого объединения будет новый для нас объект матричное дифференциальное уравнение

Правило умножения матриц, которое мы обсуждали выше, гарантирует. что матричная функция X(t) является решением матричного дифференциального уравнения, тогда и только тогда, когда ее столбцы являются, решением векторного дифференциального уравнения (с той же матрицей коэффициентов).

Еще раз отметим, что для построения решения матричного дифференциальною уравнения нет необходимости брать обязательно линейно независимую систему решений. Можно даже взять все решения нулевые получится тривиальное нулевое решение матричного дифференциального уравнения. Можно взять линейно зависимые получится решение матричного дифференциального уравнения с вырожденной матрицей. И только когда система решений линейно независима, решение матричного дифференциального уравнения оказывается невырожденной матрицей. Теорема об определителе Вронского и формула Якоби показывают, что решение матричного дифференциального уравнения либо при всех t. является вырожденной матрицей, либо при всех t является невырожденной матрицей.

Определение 19.1 Матричная функция Ф (?) называется фундаментальной матричной функцией системы (19.1), если она является решением соответствующего матричного дифференциального уравнения и невырождена.

Оправданием такого названия служит не столько то, что фундаментальная матрица составлена из фундаментальной системы решений, сколько то, что с ее помощью удается коротко записать формулу общего решения однородной векторной системы. Ведь эта формула, по существу, является линейной комбинацией столбцов нашей матрицы, а такая комбинация (это тоже один из «специальных¹¹ взглядов на свойства произведения матрицы на вектор) в точности совпадает с произведением матрицы, составленной из решений, на вектор произвольных постоянных:

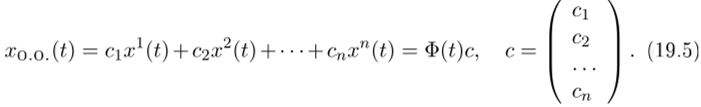
Полученная формула позволяет получить и общее решение матричного дифференциального уравнения. Пусть Ф (?) некоторая фундаментальная матрица. X (t) произвольное решение матричного дифференциального уравнения, составленное из столбцов …, xⁿ(t). По скольку каждый столбец является решением векторного дифференциального уравнения,.

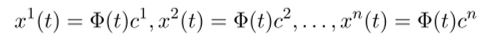
(для каждой х^г вектор констант с* свой), а эти соотношения опять же «собираются» в одно матричное:

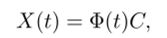
где С уже матрица, составленная из произвольных постоянных. Таким образом, формула общего решения матричного дифференциального уравнения имеет вид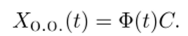

Из нее видно, в частности, что разнообразие свойств решений матричного дифференциального уравнения ограничивается именно матрицей произвольных постоянных: если она нулевая мы получаем нулевое решение. Если она вырождена вырожденное, если она невырождена невырожденное, т. е. еще одно фундаментальное решение.

• [1] На самом деле не надо обманывать себя и считать такие чудесные свойства ма тричного умножения благодатью, ниспосланной нам свыше та хорошее поведение. Вдействительности все наоборот: матричное умножение появилось в алгебре именнов такой форме потому, что она обеспечивала ряд эффективных упрощений в записиформул. В частности позволяла набор векторных соотношений «сворачивать» водно матричное.