Геометрические вероятности. 
Теория вероятностей и математическая статистика

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).

Пусть отрезок / составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположсний: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок / пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок / определяется равенством.

Пример 1. На отрезок 0/1 длины L числовой оси Ох наудачу поставлена точка В (х). Найти вероятность того, что меньший из отрезков ОБ и ВЛ имеет длину, большую 1/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

Решение. Разобьем отрезок ОЛ точками С и D на 3 равные части. Требование задачи будет выполнено, если точка В (х) попадет на отрезок CD длины 1/3. Искомая вероятность.

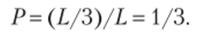
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством.

Пример 2. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.

Решение. Площадь кольца (фигуры g).

Площадь большого круга (фигуры G)

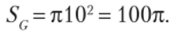
Искомая вероятность.

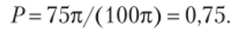
Пример 3. В сигнализатор поступают сигналы от двух устройств, причем поступление каждого из сигналов равновозможно в любой момент промежутка времени длительностью Т. Моменты поступления сигналов независимы одни от другого. Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше t (t < Т). Найти вероятность того, что сигнализатор сраоотает за время Т, если каждое из устройств пошлет, но одному сигналу.

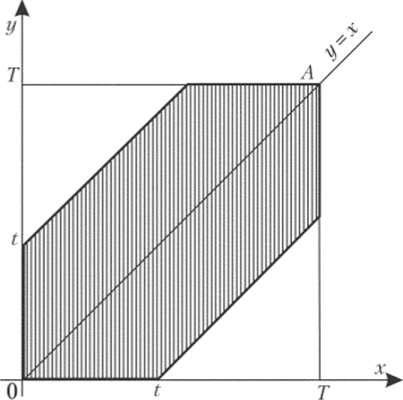
Рис. 1.

Решение. Обозначим моменты поступления сигналов первого и второго устройств соответственно через х и у. В силу условия задачи должны выполняться двойные неравенства:

О < х < T_t 0 < у < Т. Введем в рассмотрение прямоугольную систему координат хОу. В этой системе двойным неравенствам удовлетворяют координаты любой точки квадрата ОТЛТ(рис. 1).

Таким образом, этот квадрат можно рассматривать как фигуру G, координаты точек которой представляют все возможные значения моментов поступления сигналов.

Сигнализатор срабатывает, если разность между моментами поступления сигналов меньше ?, т. е. если у -х < t при у > хих-у у_у или, что-то же,.

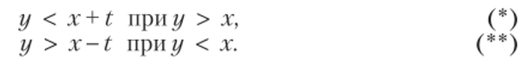
Неравенство (*) выполняется для тех точек фигуры G, которые лежат выше прямой у = х и ниже прямой у=х + V, неравенство (**) имеет место для точек, расположенных ниже прямойу-хи выше прямойy = x-t.

Как видно из рис. 1, все точки, координаты которых удовлетворяют неравенствам (*) и (**), принадлежат заштрихованному шестиугольнику. Таким образом, этот шестиугольник можно рассматривать как фи гуру g, координаты точек которой являются благоприятствующими моментами времени х и у.

Искомая вероятность.

Замечание 1.1 (риведенные определения являются частными случаями общего определения геометрической вероятности. Если обозначить меру (длину, площадь, объем) области через mes, то вероятность попадания точки, брошенной наудачу (в указанном выше смысле) в область g — часть области G, равна.

3 а м е ч, а н и е 2. В случае классического определения вероятность достоверного (невозможного) события равна единице (нулю); справедливы и обратные утверждения (например, если вероятность события равна нулю, то событие невозможно). В случае геометрического определения вероятности обратные утверждения нс имеют места. Например, вероятность попадания брошенной точки в одну определенную точку области G равна нулю, однако это событие может произойти и, следовательно, не является невозможным.