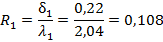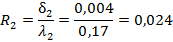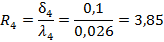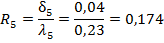Геометрические преобразования. 
Компьютерная графика

Очень распространенной задачей КГ является определение местоположения пиксела, соответствующего точке с координатами (x, y) после поворота её относительно точки (x0, y0) на угол. Пусть r — длина вектора, соединяющего точку (x, y) с точкой (x0, y03) (рис. 7). Поскольку её значение при повороте не изменяется, справедливы следующие уравнения:

X — x0 = r cos (+), (19).

Y — y0 = r sin (+).

Рис. 7. Поворот точки (х, у) на угол относительно точки (хо, уо)

Разложив косинус и синус суммы двух углов в уравнении (19) и выполнив подстановку х-x0 = rcos, y-y0 = rsin,.

получим уравнение, определяющее значение (X, Y) новых координат:

X = x0 + (х — x0) cos — (y — y0) sin;

Y = y0 + (х — x0) sin + (y — y0) cos.

В задачах компьютерной графики более удобна матричная запись. Матрицу поворота относительно начало координат можно записать.

.

Изменение масштаба производится умножением значений координат на масштабный множитель. Матрицу изменения масштаба можно записать, зная масштабные множители Sx и Sy:

.

Отражение (относительно оси абсцисс) (рис. 8):

x1= x;

y1= - y.

Матрица отражения может быть записана.

.

Рис. 8. Отражение точки относительно оси абсцисс

Перенос точки (рис. 9) легко учесть, прибавив к значениям соответствующих координат величину перемещения.

X =x + x;

Y =y + y.

Рис. 9. Перенос точки

Для того, чтобы записать матрицу переноса, необходимо ввести однородные координаты. В КГ однородные координаты вводят следующим образом: точке М (x, y) ставится в соответствие точка (x, y, 1) в пространстве (рис. 10).

Рис. 10. Ввод однородных координат

Матрица переноса может быть записана.

.

Координаты точки M1(x1,y1) могут быть подсчитаны.

.

Соответственно могут быть рассчитаны координаты точки M1 при повороте и масштабировании:

Сложное преобразование объекта можно определить как цепочку основных преобразований, применённых последовательно. Матрица сложного преобразования будет определена в виде произведения матриц преобразований, составляющих цепочку.

Вопросы и упражнения:

Что называется геометрической моделью объекта?

Какие требования предъявляются к геометрическому моделированию?

Назовите основные принципы конструирования кривых.

Какой недостаток у интерполирования полиномами?

Когда при интерполировании рекомендуется применять интерполяционный полином Ньютона?

В каких случаях рекомендуется применять интерполяционный полином Эрмита?

Какие способы задания параметрических уравнений кривых используются в компьютерной графике?

Постройте сегмент кривой Безье, представленной характерными точками P0(1,2), P1(3,4), P2(5,5), P3(8,1).

Как выполняется интерполяция кубическими сплайнами?

Какие системы координат используются в компьютерной графике?

Какие геометрические преобразования на плоскости используются в компьютерной графике?