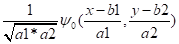Двумерные вейвлеты. 
Цифровая обработка изображений

Для работы с изображениями необходимо обрабатывать двумерные массивы данных. Для общности пусть они по-прежнему задаются в пространстве V, но теперь как функции двух переменных х и у. В этом случае вместо выражения для одномерной вейвлет-функции вида, записанной с независимой переменной х, можно воспользоваться ее двумерным аналогом, учитывая, что теперь по каждому измерению (х и у) пространства сигнала V имеются свои значения, а и b. Обозначив их как а1 и а2, а также b1 и b2, можно записать выражение для двумерного непрерывного вейвлета в виде:

.

где V = х, y? R2. Для двумерного дискретного вейвлет-анализа непрерывных сигналов необходимо также задать условия дискретизации:

(j, k)?Z², a=2^j, b=k2^j=ka,.

Ш_{j, k}=2^-j/2ш (2^-jV-k), ц_{j, k}=2^-jц (2^jV-k).

Попробуем распространить описанные выше положения частотно-временного представления вейвлет-анализа на случай сигналов в виде функций двух переменных х и у. В данном случае можно воспользоваться тензорным произведением одномерного кратномаштабного анализа, и в качестве мерной масштабирующей функции взять Ф (х, у)=ц (х)ц (у).

Тогда, с учетом известного соотношения для тензорного произведения, вместо одного вейвлета теперь возникают три:

Ш_LH(x, y)=ц (x)ш (y), Ш_HL(x, y)=ш (x)ц (y), Ш_HH(x, y)=ш (x)ш (y).

Здесь по-прежнему L означает реализацию фильтра низких частот,.

H — реализацию фильтра высоких частот.