Элементарное правило расселения

Теперь не трудно показать, что ход кривых фактического расселения может быть с достаточной точностью объяснен и предсказан теоретически.

Основания к этому объяснению уже приведены выше. Посылка первая заключается в определении управляющих расселением мест тяготения населения: она говорит, что не все места тяготения населения управляют расселением, а только места постоянного тяготения, то есть почти исключительно места постоянного приложения труда. Посылка вторая — не менее проста и наглядна: она заключается в том, что расселение ориентируется не на геометрические расстояния от места жительства до места постоянного приложения труда, а на время, которое необходимо при наличных транспортных средствах, для преодоления этих расстояний.

Обе эти посылки выше уже пояснены.

Посылка третья уже определяет характер тех количественных отношений, которые имеют здесь место. Она совершенно обща и формальна и заключается в следующем: при прочих равных условиях, изменение избранного расстояния места жительства от места приложения труда имеет не абсолютное, а относительное значение по отношению к первоначальному расстоянию, выраженному в затраченном на его преодоление времени, то есть следует общему психофизическому закону оценок других раздражителей, например, веса, яркость освещения, уровня шума и прочее. Следовательно, реакция человека на затраты времени рассматривается, как реакция физиологическая. Допустимо ли это? Укажем, прежде всего, что тем же правилам пользуется инженер-светотехник при расчете освещения; им пользуется инженер-акустик при расчете шумоизоляции стен; им пользуется химик-парфюмер при определении силы запаха; им пользуется токсиколог при определении раздражения ядовитыми веществами; тем же правилом пользуется теплотехник, применяя шкалу эффективных температур; ему следует оценка вибрации. Короче, это правило имеет широчайшее практическое приложение в технике во всех тех случаях, когда требуется оценить реакцию ощущения на те или иные раздражения. В данном случае мы применяем его к оценке значимости затраты времени.

Экспериментальной психологии давно известно, что оценки времени подчиняются этому правилу (см., например, курс психологии Эббинггаусса). И здесь, конечно, нет ничего удивительного: сколь ни многообразны мотивы, по которым человек избирает себе то или иное место жительства или место работы, — он сохраняет полностью свою природу и присущую ему методу оценок любых раздражителей, в данном случае расстояний и времени и, при прочих равных условиях или безразличных обстоятельствах, следует этим оценкам.

Следовательно, статистически, когда беспорядочное множество случаев, ориентированных только по расстояниям или времени, сглаживает все другие действующие факторы, — должны выступать зависимость расселения от расстояния и времени. Все это кажется достаточно простым и бесспорным.

Но нам нет необходимости поднимать здесь отвлеченно методологические вопросы, так сказать, «психологии расстояния». Оставаясь в рамках решения технических задач, нам вполне достаточно исходить из факта зависимости расселения от расстояния и рассматривать те формулы, которые представляют эти факты для целей технического расчёта, как формулы эмпирические, не претендующие на вскрытие существа явления.

Теперь достаточно только заметить, что расселение уменьшается с ростом расстояния, а задача математически, приёмами исчисления вероятностей становится вполне определенной.

В интервале расстояний r2 и r1 от места постоянного приложения труда, при данной скорости существующих транспортных средств v, нормально; при прочих равных условиях проживания, распределяются % трудящихся, выражаемый следующей зависимостью:

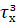
(12).

где постоянные, а и b находятся по предельным расстояниям R1 (минимум) и R2 (максимум), в которых расселение вообще возможно по условиям планировки:

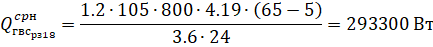
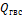
;. (13).

Даваемое в тексте решение задачи может быть получено следующим образом.

Пусть расселение, по условиям планировки, вообще возможно в пределах расстояний от I1 и I2, выраженных во времени.

Обозначим вероятность поселения на расстоянии от I1 до t через f (t).

В таком случае вероятность поселения на расстояниях от I1 до t+dt будет f (t+dt) и вероятность поселения на рассматриваемом расстоянии (по теореме сложения вероятностей и строке Тейлора) будет:

(14).

Вероятность поселения в интервале расстояний t1 и t2 будет:

(15).

Так как расселение в границах планировки I1 и I2 достоверно, на дальней же границе I2 вероятность поселения стремиться к нулю, то.

P (J1, J2) = ?J1J2 (16).

? (J2) = 0 (17).

Что касается вида функции ?(t), то он определяется условием третьим, приведенным в тексте.

d? (t) = - a (dt/t).

откуда.

? (t) = b — a lnt (18).

где, а и b постоянные, определяемые на приведенных условий (16 и 17).

Условия (16, 17 и 18) дают следующие уравнения для определения постоянных:

(J2) = b — a ln J2 = 0.

.

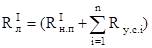
где е — основание непаровых логарифмов (в нашем случае достаточно принять е ~2,7).

Отсюда:

.

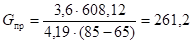
Логарифмы натуральные.

Количество живущих в интервале расстояний t1 и t2, выраженное в %, находим непосредственно по вероятности поселения в том же интервале (15 и 18) путем умножения ее на 100:

.

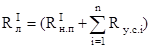
Переходя от натуральных логарифмов к десятичным (модуль 2, 3) и от времени к расстояниям с помощью очевидного соотношения t = r/?, где r расстояние и? скорость сообщения, и получим выражения, данные в тексте.

Формулы эти впервые получены автором еще в 1933 году и опубликованы в его работе «Планировка, транспорт и расселение», Харьков 1934 года, стеклографическ. изд.

Минимальное возможное расстояние R1, на котором возможно поселение, очевидно представляет собою ширину зоны разрыва между местом приложения труда и селитьбой. Эта величина практически может колебаться от 0 до 2-х км. Максимальное расстояние R2, на котором поселение еще возможно, условимся выражать в минутах времени, которые необходимы на преодоление этого расстояния с принятой скоростью городского сообщения. Это расстояние чаще всего принимается равным 60 минутам, реже 45 мин. Величины R1 и R2 так же как и ?, являются величинами установочными, проектными и выражающими в конкретных цифрах ту степень удобства расселения, с которой мы начали выше рассмотрение всего вопроса.

Проверку только что приведенного элементарного правила расселения произведем тем же способом, что и выше, т. е. путем построения на его основе теоретической кривой распределения пассажиров по дальности поездки и сравнения ее с фактической кривой для Ленинграда. Это сравнение и сделано на рис. 9.

Сравнение этого свидетельствует об очень хорошем совпадении, полученной совершенно абстрактным путем кривой со статистической кривой, полученной из самой гущи опыта. И нужно не писать, разумеется, никакого уважения к законам случая, если столь полное совпадение обоих кривых приписывать случайности. Оно, напротив, является убеждающим доказательством того, что приведенное теоретическое объяснение кривых расселения в своей основе правильно отражает факты.

Элементарное правило расселения (12 и 13) устанавливает в явной форме зависимость расселения от расстояния и принятой скорости сообщения. Но, как следует из оснований вывода этих формул, расселение должно определяться только в функции времени, затрачиваемого на передвижение. И действительно, исключая из (12 и 13) расстояния через время и скорость (r = ?t), получаем эквивалентную (12 и 13) формулу элементарного правила расселения в зависимости только от времени, затрачиваемого жителями города на передвижение:

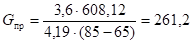
(19).

где (20).

По этим формулам находится расстояние в %% в интервале времени на передвижение от места жительства к месту работы от t1 до t2, при условии, что расселение возможно в интервале времени от J1 до J2.