Предмет теории вероятностей

Теория вероятностей исследует закономерности, возникающие в случайных опытах (явлениях). Случайным именуют опыт, итог которого нельзя предсказать заблаговременно. Неосуществимость предсказать заблаговременно — основное, что отличает случайное явление от детерминированного.

Не все случайные явления (опыты) разрешено изучать способами теории вероятностей, а только те, которые имеют все шансы быть воспроизведены в 1 и тех же критериях и владеют (почему-то как проверяемым заблаговременно) свойством «статистической устойчивости: «если, А — некое явление, могущее произойти либо никак не случится в итоге опыта, то порция n (А)/n числа опытов, в которых данное явление произошло, имеет тенденцию стабилизироваться с подъемом общего количества опытов n, приближаясь к некоторому количеству Р (А). Наверное количество служит объективной чертой «степени возможности» событию, А произойти.

В предстоящем мы станем говорить только о случайных экспериментах, обладающих данными качествами, а свойство статистической устойчивости докажем в утверждении, известном как закон больших чисел Бернулли.

Приведем примеры случайных явлений.

1. Производится стрельба из орудия, установленного под заданным углом к горизонту.

Воспользовавшись способами внешней баллистики (науки о движении снаряда в воздухе), разрешено найти теоретическую линию движения снаряда. Данная линия движения вполне определяется условиями стрельбы: исходной скоростью снаряда, углом кидания и баллистическим коэффициентом снаряда. Фактическая линия движения всякого отдельного снаряда неизбежно несколько отклоняется от теоретической за счет совокупного воздействия многих факторов. Среди этих факторов можно, к примеру, назвать: оплошности производства снаряда, отклонение веса заряда от номинала, разнородность структуры заряда, оплошности установки ствола в заданное положение, метеорологические условия и т. д. Если изготовить несколько выстрелов при неизменных основных условиях (,), мы получим не 1 теоретическую линию движения, а целый пучок либо «сноп» траекторий, образующих так именуемое «рассеивание снарядов».

• 2. Одно и то же тело некоторое количество раз взвешивается на аналитических весах; итоги повторных взвешиваний несколько различаются друг от друга. Эти различия обусловлены воздействием многих второстепенных причин, сопровождающих операцию взвешивания, таких, как состояние тела на чашке весов, случайные вибрации техники, оплошности отсчета показаний устройств и т. д.
• 3. Самолет совершает полет на заданной высоте; теоретически он летит горизонтально, умеренно и прямолинейно. Практически полет сопровождается отклонениями центра массы самолета от теоретической линии движения и колебаниям самолета около центра массы. Эти отклонения и колебания считаются случайными и связаны с турбулентностью атмосферы; от раза к разу они не повторяются.
• 4. Делается ряд подрывов осколочного снаряда в конкретном расположении относительно цели. Итоги отдельных подрывов несколько различаются друг от друга: изменяются общее количество осколков, взаимное расположение их траекторий, вес, форма и скорость каждого отдельного осколка. Данные изменения считаются случайными и связаны с воздействием таких факторов, как неоднородность металла корпуса снаряда, неоднородность взрывчатого вещества, непостоянство скорости детонации и т. п. В связи с этим разные подрывы, осуществленные, казалось бы, в одинаковых критериях, могут приводить к разным итогам: в 1 подрывах цель станет поражена осколками, в остальных — нет.

Все приведенные примеры рассмотрены тут под одним и тем же углом зрения: подчеркнуты случайные вариации, неодинаковые итоги ряда экспериментов, основные условия которых остаются постоянными. Данные вариации постоянно связаны с наличием каких-то второстепенных факторов, оказывающих большое влияние на финал эксперимента, но не заданных в количестве его основных критерий. Основные условия эксперимента, характеризующие в общих и грубых чертах его протекание, сохраняются постоянными; второстепенные — изменяются от эксперимента к эксперименту и вносят случайные отличия в их итоги.

Совершенно очевидно, что в природе нет ни 1-го физического явления, в котором никак не присутствовали бы в той или иной мере составляющие случайности. Как бы точно и подробно ни были фиксированы условия эксперимента, нереально добиться того, чтоб при повторении эксперимента итоги полностью и в точности были схожими.

Случайные отличия неизбежно сопровождают любому закономерному действу. Тем не менее, в ряде практических задач этими случайными элементами можно пренебречь, рассматривая вместо реального явления его упрощенную схему, «модель», и предполагая, что в этих критериях эксперимента явление проходит вполне конкретным образом. При этом из бесчисленного большого колличества факторов, оказывающих большое влияние на данное явление, выделяются наиболее главные, основные, решающие; воздействием остальных, второстепенных факторов просто пренебрегают. Такая методика исследования явлений постоянно используется в физике, механике, технике. При пользовании данной схемой для решения хоть какой задачи прежде всего выделяется основной круг учитываемых критерий и выясняется, на какие характеристики задачи они влияют; затем используется тот либо другой математический аппарат (к примеру, составляются и интегрируются дифференциальные уравнения, описывающие явление); таким образом выявляется основная закономерность, характерная этому явлению и дающая вероятность предречь итог эксперимента по его заданным условиям. По мере становления науки количество учитываемых причин становится все больше; явление изучается подробнее; научный прогноз становится точнее.

Но для решения ряда вопросов описанная методика — классическая методика так именуемых «точных наук» — как оказалось плохо адаптированной. Есть такие задачи, где интересующий нас финал эксперимента находится в зависимости от столь огромного количества факторов, что практически нереально зарегистрировать и учесть все данные причины. Это — задачи, в которых многочисленные второстепенные, тесно переплетающиеся меж собой случайные причины играют заметную роль, а вместе с тем количество их так велико и влияние настолько сложно, что использование классических способов изучения себя не оправдывает.

Рассмотрим пример. Производится стрельба по некой цели Ц из орудия, установленного под углом к горизонту. Линии движения снарядов, как было указано выше, не схожи между собой; в итоге точки падения снарядов на земле рассеиваются. Если размеры цели велики по сопоставлению с областью рассеивания, то этим рассеиванием, очевидно, можно пренебречь: при правильной установке орудия хоть какой выпущенный снаряд попадает в мишень. Если же (как обычно и бывает на практике) область рассеивания снарядов превышает габариты цели, то некоторые из снарядов в взаимосвязи с воздействием случайных причин в мишень не попадут. Появляется ряд вопросов, к примеру: какой процент выпущенных снарядов в среднем попадает в мишень? Насколько необходимо потратить снарядов для того, чтоб достаточно надежно поразить мишень? Какие надлежит принять меры для уменьшения расхода снарядов?

Чтобы ответить на подобные вопросы, обычная схема точных наук оказывается недостаточной. Данные вопросы органически связаны со случайной природой явления; для того, чтобы на них ответить, разумеется, невозможно просто пренебречь случайностью, — нужно изучить случайное явление рассеивания снарядов с точки зрения закономерностей, свойственных ему именно как случайному явлению. Нужно изучить закон, по которому распределяются точки падения снарядов; необходимо выяснить случайные причины, вызывающие рассеивание, сопоставить их между собой по ступени значимости и т. д.

Рассмотрим другой пример. Некоторое техническое приспособление, к примеру, система автоматического управления, решает конкретную задачу в условиях, когда на систему постоянно действуют случайные помехи. Присутствие помех приводит к тому, что система решает задачу с некоторой ошибкой, в ряде случаев выходящей за пределы возможной. Появляются вопросы: как часто станут возникать эти ошибки? Какие следует принять меры для того, чтобы практически исключить их вероятность?

Чтобы ответить на эти вопросы, нужно исследовать природу и структуру случайных возмущений, воздействующих на систему, изучить реакцию системы на эти возмущения, выяснить воздействие конструктивных характеристик системы на вид данной реакции.

Все подобные задачи, количество которых в физике и технике чрезвычайно велико, требуют исследования не только основных, главных закономерностей, характеризующих явление в общих чертах, но и анализа случайных возмущений и искажений, связанных с наличием второстепенных факторов и придающих финалу эксперимента при заданных критериях элемент неопределенности.

Пример. Один раз подбрасывается 1 игральная кость (кубик). Самый разумный метод установить пространство элементарных исходов таков: Щ = {1,2,3,4,5,6}, элементарные исходы здесь соответствуют числу выпавших очков.

Примеры событий: А = {1,2} - выпало одно либо 2 очка; А = {1,3,5} - выпало нечетное количество очков.

Пример. 2 раза подбрасывается 1 игральная кость (кубик). Либо, что, то же наиболее, один раз подбрасываются 2 игральные кости. Как мы увидим в предстоящем, здесь самый разумный метод установить место элементарных исходов — считать итогом опыта упорядоченную пару количеств (i, j), в которой 1 i, j 6и i — число очков выпавших первый раз, j — число очков, выпавших второй раз. Щ = {(i, j), где 1 i, j 6}.

Примеры событий:

А = {(1,1), (1,2), (1,3), (1,4), (1,5), (1,6)} - при первом подбрасывании выпало одно очко;

А = {(1,1),(2,2), (3,3), (4,4), (5,5), (6,6)} - при двух подбрасываниях выпало одинаковое число очков.

Пример. На плоскость стола бросается монетка. Итогом опыта разрешено полагать координату центра монеты (а если нам не безразличен угол поворота монеты, то разрешено добавить и величину данного угла). Пространство элементарных исходов — множество точек стола (в другом случае — очень много пар {х, ц}, где х — координата точки стола ц [0, 2р]- угол поворота). Количество элементарных исходов такового опыта несчетно.

Пример. Монетка подбрасывается по тех пор, пока не выпадет вверх гербом. Место элементарных исходов состоит из бесконечного, но счетного количества исходов:

Щ = {г, рг, ррг, рррг, ррррг, рррррг, …}, где р и г означают выпадение решки и герба при одном подкидывании, соответственно.

Пример. Приведем пример неправильно выбранного места элементарных событий. Пусть при кидания игральной кости Ч = {четное количество очков}, Т = {количество очков, кратное 3}. Тогда Щ = {Ч, Т, 1, 5} составляет все исходы опыта, однако исходы Ч и Т могут наступать одновременно.

• 1) Достоверным именуется явление, которое обязательно проистекает в итоге опыта, то есть единственное явление, включающее все без исключения элементарные исходы — событие Щ.
• 2) Невозможным именуется явление которое никак не имеет возможность произойти в итоге опыта, то есть явление, не содержащее ни 1-го элементарного исхода («пустое множество»). Заметим, что постоянно Щ.

Пусть, А и В — событие.

• 1) Объединением, А U В событий, А и В именуется явление, состоящее в том, что произошло или, А, или В, или оба действия сразу. На языке теории множеств, А U В имеется очень много, содержащее как элементарные исходы, входящие в А, так и элементарные исходы, входящие в В.
• 2) Пересечением, А? В событий, А и В именуется событие, состоящее в том, что случились оба действия, А и В одновременно. То имеется, А? В имеется множество, содержащее элементарные исходы, входящие одновременно в, А и в В.
• 3) Дополнением АВ действия, А по В именуется явление, состоящее в том, что произошло явление А, но не произошло В. То имеется АВ есть множество, содержащее элементарные исходы, входящие в А, однако никак не входящие в В.
• 4) Противоположным к событию, А именуется явление, состоящее в том, что явление, А в итоге опыта никак не произошло. Иначе говоря, имеется очень много, содержащее элементарные исходы, никак не входящие в А.
• 1) События, А и В называются несовместными, если, А? В = .
• 2) События А₁, А₂, … А_n называются попарно несовместными, если для любых i? j, 1 i, j n, события А_iи А_j несовместны.
• 3) Говорят, что явление, А влечет явление В, и пишут, А В, если постоянно, как только проистекает явление А, проистекает и явление В. На языке теории множеств это значит, что любой элементарный исход, поступающий в А, сразу входит и в явление В.

Вероятность на дискретном пространстве элементарных исходов Допустим, что мы имеем дело с дискретным пространством элементарных исходов, то есть пространством, состоящим из конечного либо счетного числа элементов:

Щ = {щ_1, щ₂, … щ_n, … }.

Поставим каждому элементарному исходу щ_i Щ в соответствие число р (щ_i) [0,1] так, что.

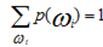(15).

Назовем число р (щ_i) вероятностью элементарного исхода щ_i. Вероятностью события, А Щ называется число.

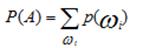(16).

равное сумме возможностей элементарных исходов, входящих в очень много А.

Позднее, познакомившись с аксиоматикой теории возможностей, мы установим вероятности событий непосредственно, а никак не через вероятности элементарных исходов. Тем более что сложением возможностей элементарных исходов разрешено заполучить только вероятность события, состоящего никак не более чем из счетного количества элементарных исходов (иначе само понятие суммирования никак не определено). Однако на дискретном пространстве элементарных исходов определить вероятности событий так, как это сделано в определении 6, постоянно возможно.

Перечислим очевидные в случае дискретного пространства элементарных исходов характеристики вероятности, которые мы скоро докажем сразу в общем случае.

• 1) 0 Р (А) 1;
• 2) Р (Щ) = 1;
• 3) Р () = 0;
• 4) Р (Ф) = 1 — Р (О);
• 5) если, А и В несовместны, то Р (А U В) = Р (А) + Р (В);
• 6) в общем же случае Р (А U В) = Р (А) + Р (В) — Р (А? В);
• 7) если, А В, то Р (А) Р (В).