Аппроксимация функций. 
Элементы теории погрешностей. 
Интерполяция и аппроксимация функций

Постановка задачи

Иногда возникает необходимость аппроксимации данной функции другими функциям, которые легче вычислить. В частности, рассматривается задача о наилучшем приближении в нормированном пространстве Н, когда заданную функцию f требуется заменить линейной комбинацией заданных элементов из Н так, чтобы отклонение ||f — || было минимальным.

Метод наименьших квадратов

Mетод наименьших квадратов был предложен Гауссом и Лежандром в конце XVIII — начале XIX веков в связи с проблемой обработки экспериментальных данных. В этом случае задача построения функции непрерывного аргумента по дискретной информации, характеризуется двумя особенностями:

• 1. Число точек, в которых проводятся измерения, обычно бывает достаточно большим.
• 2. Значения функции в точках сетки определяются приближенно в связи с неизбежными ошибками измерения.

С учетом этих обстоятельств строить функцию в виде суммы большого числа слагаемых и добиваться ее точного равенства в точках сетки величинам, как это делалось при интерполировании, становится нецелесообразным.

В методе наименьших квадратов аппроксимирующая функция ищется в виде суммы, аналогичной, но содержащей сравнительно небольшое число слагаемых.

.

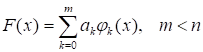
погрешность уравнение интерполяция в частности, возможен вариант .

Предположим, что мы каким-то образом выбрали коэффициенты, тогда в каждой точке сетки, можно подсчитать погрешность.

.

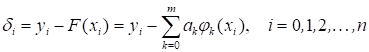
Сумма квадратов этих величин называется суммарной квадратичной погрешностью.

.

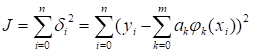
Она дает количественную оценку того, насколько близки значения функции в точках сетки к величинам .

Меняя значения коэффициентов, мы будем менять погрешность, которая является их функцией. В результате естественно возникает задача:

Найти такой, набор коэффициентов, при которых суммарная квадратичная погрешность оказывается минимальной.

Функцию с набором коэффициентов, удовлетворяющих этому требованию, называют наилучшим приближением по методу наименьших квадратов.

Построение наилучшего приближения сводится к классической задаче математического анализа об экстремуме функции нескольких переменных. Метод решения этой задачи известен.

Необходимым условием экстремума является равенство нулю в экстремальном точке всех первых частных производных рассматриваемой функции. В случае это дает.

.

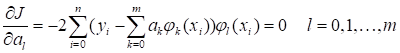
Оставим члены, содержащие, слева и поменяем в них порядок суммирования по индексам и. Члены, содержащие, перенесем направо. В результате уравнения примут вид.

.

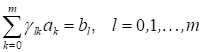
где.

.

.

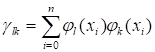
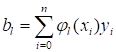
Мы получили систему линейных алгебраических уравнений, в которой роль неизвестных играют искомые коэффициенты разложения. Число уравнении и число неизвестных в этой системе совпадает и равно. Матрица коэффициентов системы Г состоит из элементов, которые определяются формулой. Ее называют матрицей Грама для системы функций на сетке. Отметим, что матрица Грама является симметричной: для ее элементов, согласно, справедливо равенство. Числа, стоящие в правой части уравнений, вычисляются по формуле через значения сеточной функции .

Предположим, что функции выбраны такими, что определитель матрицы Грама, отличен от нуля:

.

В этом случае при любой правой части система имеет единственное решение.

.

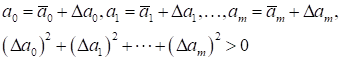
Рассмотрим наряду с набором коэффициентов, полученных в результате решения системы, любой другой набор коэффициентов. Представим числа в виде и сравним значения суммарной квадратичной погрешности для функций, построенных с помощью коэффициентов и .

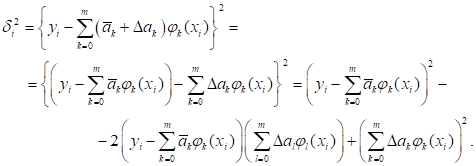
Квадрат погрешности и точке для функции с коэффициентами можно записать в виде Здесь в среднем слагаемом мы заменили в одной из сумм индекс суммирования на, чтобы не использовать один и тот же индекс в двух разных суммах и иметь возможность перемножить их почленно.

Чтобы получить суммарную квадратичную погрешность, нужно просуммировать выражения для по индексу Первые слагаемые не содержат. Их сумма дает погрешность, вычисленную для функции с коэффициентами .

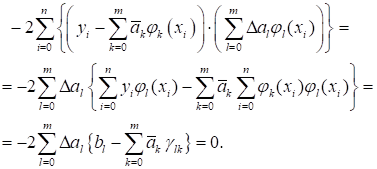
Рассмотрим теперь сумму вторых слагаемых, которые зависят от линейно:

Здесь мы поменяли местами порядок суммирования и воспользовались тем, что коэффициенты, удовлетворяют системе уравнений .

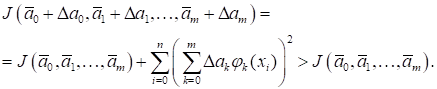
С учетом будем иметь Формула показывает, что функция с коэффициентами, полученными в результате решения уравнений, действительно минимизирует суммарную квадратичную погрешность. Если мы возьмем любой другой набор коэффициентов, отличный от, то согласно формуле к погрешности добавится положительное слагаемое и она увеличится.

Итак, чтобы построить наилучшее приближение сеточной функции, по методу наименьших квадратов, нужно взять в качестве коэффициентов разложения решение системы линейных уравнений .