Характеристики коллекторов. 
Подземная нефтегазовая гидродинамика

С точки зрения теории фильтрации значение твердого скелета горной породы, прежде всего, геометрическое, он ограничивает ту область пространства, в которой движется жидкость. Лишь только в отдельных случаях приходится рассматривать силовое взаимодействие между скелетом и прилегающей к нему жидкостью. Поэтому свойства горных пород в теории фильтрации описываются некоторым набором геометрических характеристик, осредненных по достаточно малому, по сравнению с исследуемым объемом, но содержащему большое число элементов (частиц, пор, трещин).

Параметры пористой среды. Важнейшая характеристика — полная пористость «mо «, равная отношению объема пор Vп к общему объему элемента V.

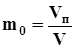
. (1.1).

В связи с тем, что переток жидкости осуществляется через поверхность, представляется необходимым введение параметра, связанного с площадью. Такой геометрический параметр называется просветностью «ms «и определяется как отношение площади просветов Fп ко всей площади сечения образца F.

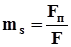
. (1.2).

Пользоваться такими поверхностными параметрами практически не представляется возможным, так как в реальных породах они меняются от сечения к сечению и определить их можно только с помощью микроскопического анализа. Следовательно, желательно данные параметры заменить на объемные, которые можно определить достаточно надежно. Выше отмечалось, что породы можно разделить на изотропные и анизотропные. Для анизотропных коллекторов с упорядоченной структурой данные параметры нельзя заменять на объемные. Для хаотичных, изотропных сред указанная замена возможна и просветность полагают равной пористости.

В пористой среде есть тупиковые и замкнутые поры, в которых движения жидкости не происходит. В связи с этим, вполне обосновано введение понятия открытой пористости, которая описывается соотношением (1.1), но под Vп понимается объём открытых пор Vпo.

В реальных условиях твердые зерна породы обволакиваются тонкой плёнкой, остающейся неподвижной даже при значительных градиентах давления. В этом случае подвижный флюид занимает объём, меньший Vпo и, поэтому, наряду с открытой пористостью часто пользуются понятием динамической пористости.

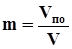
(1.3).

где Vпо — объем, занятый подвижной жидкостью.

В дальнейшем, под пористостью мы будем понимать динамическую пористость, кроме специально оговорённых случаев.

Пористость твердых материалов (песок, бокситы и т. д.) меняется незначительно при изменении даже больших давлений, но пористость, например, глины очень восприимчива к сжатию. Так пористость глинистого сланца при обычном давлении равна 0.4 — 0.5, а на глубине 1800м — 0.05. Для газовых и нефтяных коллекторов в большинстве случаев m=15−22%, но может меняться в широких пределах: от нескольких долей процента до 52%.

Для фиктивного грунта, исходя из геометрических построений, Слихтер вывел зависимость для полной пористости.

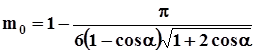
. (1.4).

Из формулы (1.4) имеем: mo=0,259 при =60о и mo=0,476 при =90о.

Просветность ms фиктивного грунта вычисляется по формуле.

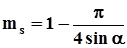
(1.5).

что даёт ms=0,0931 при =60о и ms=0,476 при =90о.

Таким образом, из формул (1.4) и (1.5) следует, что пористость и просветность фиктивного грунта не зависят от диаметра шарообразных частиц, а зависят только от степени укладки. Для реальных сред коэффициент пористости зависит от плотности укладки частиц и их размера — чем меньше размер зёрен, тем больше пористость. Последнее связано с ростом образования сводовых структур при уменьшении размера частиц.

В идеализированном представлении коэффициент пористости одинаков для геометрически подобных сред; он не характеризует размеры пор и структуру порового пространства. Поэтому для того, чтобы формулы, описывающие фиктивный грунт, можно было применить для описания реальной среды, вводится линейный размер порового пространства, а именно, некоторый средний размер порового канала или отдельного зерна пористого скелета d.

Простейшая геометрическая характеристика пористой среды — эффективный диаметр частиц грунта. Определяют его различными способами — микроскопическим, ситовым, осаждением в жидкости (седиментационным) и так далее. Эффективным диаметром частиц dэ, слагающих реальную пористую среду, называют такой диаметр шаров, образующих эквивалентный фиктивный грунт, при котором гидравлическое сопротивление, оказываемое фильтрующейся жидкости в реальном и эквивалентном грунте, одинаково. Эффективный диаметр определяют по гранулометрическому составу (рис. 1.5), например, по формуле веса средней частицы.

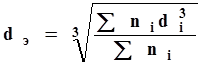
(1.6).

где di — средний диаметр iй фракции; ni — массовая или счетная доля i — й фракции.

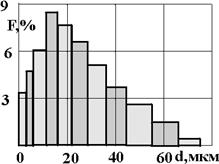
Рис. 1.5. Гистограмма распределения частиц по размерам

Для того, чтобы привести в соответствие диаметр, определённый ситовым или микроскопическим методами, с сопротивлением коллектора потоку флюида данный диаметр умножают на коэффициент гидравлической формы. Если же диаметры определяются гидродинамическими (седиментационными) методами, то они не требуют указанного уточнения.

Эффективный диаметр является важной, но не исчерпывающей характеристикой пористой среды, потому что он не даёт представления об укладке частиц, их форме. В то же время два образца грунта, имеющих одинаковые эффективные диаметры, но различную форму частиц и структуру укладки, имеют различные фильтрационные характеристики.

Таким образом, для определения геометрической структуры пористой среды, кроме пористости и эффективного диаметра, нужны дополнительные объективные характеристики. Одной из таких характеристик является гидравлический радиус пор R. Для идеального грунта имеется связь радиуса пор с диаметром частиц фиктивного грунта.

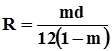
. (1.7).

Динамика фильтрационного течения, в основном, определяется трением флюида о скелет коллекторов, которое зависит от площади поверхности частиц грунта. В связи с этим, одним из важнейших параметров является удельная поверхность Sуд, то есть суммарная площадь поверхности частиц, содержащихся в единице объёма. Для фиктивного грунта.

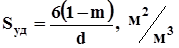
. (1.8).

Удельная поверхность нефтесодержащих пород с достаточной точностью определяется формулой.

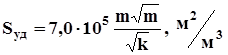
(1.9).

где k — проницаемость в дарси [мкм2].

Среднее значение Sуд для нефтесодержащих пород изменяется в пределах 40тыс. — 230тыс. м2/м3. Породы с удельной поверхностью больше 230тыс. м2/м3 непроницаемы или слабопроницаемы (глины, глинистые пески и так далее).

В практике нефтегазодобычи помимо чисто геометрической характеристики доли пустот (пористости) вводят параметры, связанные с наличием нефти, газа или воды:

а) насыщенность — отношение объёма Vf данного флюида, содержащегося в порах, к объёму пор Vп.

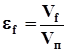
. (1.10).

По виду флюида различают нефтенасыщенность, газонасыщенность, водонасыщенность.

б) связанность — отношение объёма, связанного с породой флюида Vfс, к объёму пор

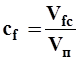
. (1.11).

Важнейшей характеристикой фильтрационных свойств породы является проницаемость. Проницаемость — параметр породы, характеризующий её способность пропускать к забою скважины флюиды. Различают проницаемости: абсолютную, эффективную или фазовую и относительную. Абсолютная проницаемость — свойство породы и не зависит от свойств фильтрующегося флюида и перепада давления, если нет взаимодействия флюидов с породой. Фазовой называется проницаемость пород для данного флюида при наличии в порах многофазных систем. Значение её зависит не только от физических свойств пород, но также от степени насыщенности порового пространства флюидами и их физических свойств. Относительной проницаемостью называется отношение фазовой к абсолютной. Проницаемость измеряется: в системе СИ — м2; технической системе — дарси (д); 1д=1,02мкм2=1,02 .10−12м2.

Физический смысл проницаемости k заключается в том, что проницаемость характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация.

Величина проницаемости зависит от размера пор для модели идеального грунта с трубками радиуса R.

k=mR2/8, (1.12).

где R — мкм; k — д.

Для реальных сред радиус пор связан с проницаемостью формулой Котяхова.

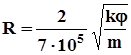
(1.13).

где kд; R — м; - структурный коэффициент (=0.5035/m1,1 — для зернистых сред).

Проницаемость песчаных коллекторов обычно находится в пределах k=100−1000мд, а для глин характерны значения проницаемости в тысячные доли миллидарси.

Проницаемость определяется геометрической структурой пористой среды, т. е. размерами и формой частиц, и системой их упаковки.

Имеется множество попыток теоретически установить зависимость проницаемости от этих характеристик, исходя из закона Пуазейля для ламинарного движения в трубах и Стокса для обтекания частиц при той или иной схематизированной модели пористой среды. Поскольку реальные породы не укладываются в рамки этих геометрических моделей, то теоретические расчеты проницаемости ненадёжны. Поэтому обычно проницаемость определяют опытным путём.

Так как радиус пор связан с удельной поверхностью, то с ней связана и проницаемость.

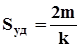
(1.14).

где при выводе учтены формулы (1.7) (1.8) и (1.12).

Параметры трещинной среды. Аналогом пористости для трещинных сред является трещиноватость mт или, иначе, коэффициент трещиноватости. Иногда данный параметр называют трещинной пористостью. Трещиноватостью называют отношение объёма трещин Vт ко всему объёму V трещинной среды.

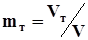
. (1.15).

Для трещинно-пористой среды вводят суммарную (общую) пористость, прибавляя к трещиноватости пористость блоков.

Второй важный параметр — густота. Густота трещин Гтэто отношение полной длины li всех трещин, находящихся в данном сечении трещинной породы к удвоенной площади сечения f.

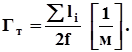
(1.16).

Из (1.16) следует, что для идеализированной трещинной среды.

mт = Гт, (1.17).

где т — раскрытость; - безразмерный коэффициент, равный 1,2, 3 для одномерного, плоского и пространственного случаев, соответственно.

Для реальных пород значение коэффициента зависит от геометрии систем трещин в породе.

Для квадратной сетки трещин (плоский случай) Гт=1 / lт, где lтразмер блока породы. Средняя длина трещин l * равняется среднему размеру блока породы и равна.

l*=1 / Гт. (1.18).

В качестве раскрытости (ширины трещины) берут среднюю величину по количеству трещин в сечении f. Среднюю гидравлическую ширину определяют, исходя из гидравлического параметра — проводимости системы трещин. Ширина трещин существенно зависит от одновременного влияния следующих двух факторов, обусловленных изменением давления жидкости, действующего на поверхность трещин:

увеличение объёма зёрен (пористых блоков) с падением давления жидкости;

увеличение сжимающих усилий на скелет продуктивного пласта.

Указанные факторы возникают из-за того, что в трещиноватых пластах горное давление, определяющее общее напряжённое состояние среды, уравновешивается напряжениями в скелете породы и пластового давления (давлением жидкости в трещинах). При постоянстве горного давления снижение пластового давления при отборе жидкости из пласта приводит к увеличению нагрузки на скелет среды. Одновременно с уменьшением пластового давления уменьшаются усилия, сжимающие пористые блоки трещиноватой породы.

Поэтому трещинный пласт — деформируемая среда. В первом приближении можно считать.

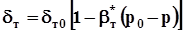
(1.19).

где т0 — ширина трещины при начальном давлении р0; *т=п l /т0 — сжимаемость трещины; п — сжимаемость материалов блоков; l — среднее расстояние между трещинами.

Для трещинных сред l/ т >100 и поэтому сжимаемость трещин высока.