Общая задача линейного программирования

Рассмотренные выше примеры задач линейного программирования позволяют сформулировать общую задачу линейного программирования.

Дана система линейных уравнений и неравенства с переменными.

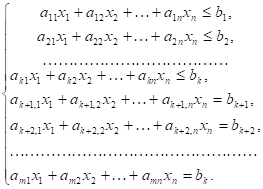
(20).

и линейная функция.

(21).

Необходимо найти такое решение системы, где.

(22).

При котором линейная функция принимает оптимальное (т.е. максимальное или минимальное) значение.

Система (20) называется системой ограничений, а функция? линейной функцией, линейной формой, целевой функцией или функцией цели.

Более кратко общую задачу линейного программирования можно представить в виде:

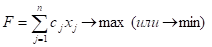
При ограничениях:

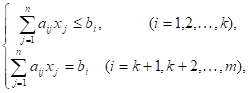
Оптимальное решение (или оптимальным планом) задачи линейного программирования называется решение система ограничений (20), удовлетворяющее условию (22), при котором линейная функция (21) принимает оптимальное (максимальное или минимальное) значение.

Термины «решение» и «план»? синонимы, однако первый используется чаще, когда речь идет о формальной стороне задачи (ее математическая решении), а второй — содержательной стороне (экономической интерпретации).

При условии, что все переменные неотрицательны, система ограничений (20) состоит лишь из одних неравенств,? такая задача линейного программирования называется стандартной; если система ограничений состоит из одних уравнений, то задача называется канонической. Так, в приведенных выше примерах задач линейного программирования задачи 1 и 2? стандартные, задача 4 —каноническая, а задача 3 — общая.

Любая задача линейного программирования может быть сведена к канонической, стандартной или общей задаче. Рассмотрим в начале вспомогательную теорему.

Теорема 1.1. всякую решению неравенства.

(23).

Соответствует определенное решение уравнения.

(24).

В котором.

(25).

И, наоборот, каждому решению уравнения (24) и неравенства (25) соответствует определенное решение неравенства (23).

Используя эту теорему (которую принимаем без доказательство), представим в качестве примера стандартную задачу (4)-(6) в каноническом виде. С той целью в каждое из неравенств системы ограничений (4) введем дополнительные неотрицательные переменные и система ограничений (4) примет вид:

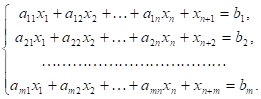
(26).

Таким образом, стандартная задача (4) — (6) в канонической форме: найти такое решение, удовлетворяющее системе (26) и условию (5), пи котором функция (6) принимает максимальное значение.

Замечание. B рассматриваемой задаче все неравенства вида "? «, поэтому дополнительные неотрицательные переменные вводились со знаком «+», в случае неравенства вида «?», соответствующие дополнительные переменные следовало бы ввести со знаком «?».

Опорный план транспортной задачи.

Определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Этот план, как уже отмечалось выше, находят методом северно-западного угла, методом минимального элемента или методом аппроксимация Фогеля. Сущность этих методов состоит в том, что опорный план находят последовательно за шагов, на каждом из которых в таблице условий задачи заполняет одну клетку, которую называет занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находиться заполненная клетка), либо вызов груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка).

В первом случае, временно исключают из рассмотрения столбец, содержащий заполненную на данном шаге клетку, и рассматривают задачу, таблица условий которой, содержит на один столбец меньше, чем было перед этим шагом, но то же количество строк и соответственно измененные запасы груза в одном из пунктов отправления (в том, за счет запаса которого была удовлетворена потребность в грузе пункта назначения на данном шаге). Во втором случае временно исключают и рассмотрения строку, содержащую заполненную клетку, и считают, что таблица условий имеет на одну строку меньше при неизменном количество столбцов при соответствующим изменении потребности в грузе в пункте назначения, в столбце которого находится заполняемая клетка.

После того как проделаны описанных выше шагов, получают задачу с одним пунктом отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта назначения. Заполнив эту клетку, тем самым делаю ()-й шаг получают искомый опорный план. Следует, заметит, что некотором шаге (но не последнем) может оказаться, что потребности очередного пункта назначения запасам очередного пункта отправления. В этом случае также временно исключает из рассмотрения либо столбца, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение занятых клеток, в котором стоят компоненты опорного плана, что является исходным условием для проверки последнего на оптимальность и нахождения оптимального плана.

Математическая модель транспортной задачи.

Однородный груз сосредоточен у поставщиков в объемах данный груз необходимо, доставить потребителям в объемах .

Известны? стоимости перевозки единицы груза от каждого поставщика j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны. Исходные данные транспортной задачи записываются в таблице вида:

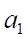
Переменными (неизвестными) транспортной задачи являются? объемы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок:

.

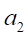
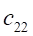
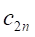
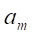
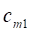
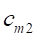
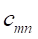
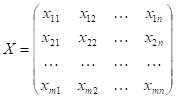
Математическая модель транспортной задачи в общем случае имеет вид:

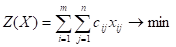
(27).

(28).

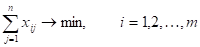
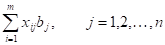
(29).

(30).

Целевая функция задачи (27) выражает требование обеспечить минимум суммарных затрат на перевозку всех грузов. Первая группа из уравнений (28) описывает тот факт, что запасы всех поставщиков вывозятся полностью. Вторая группа из уравнений (29) выражает требование полностью удовлетворить запросы всех потребителей. Неравенство (30) является условиями не отрицательности всех переменных задачи. Таким образом, математическая формулировка транспортной задачи состоит в следующем: найти переменные задачи Удовлетворяющие системе ограничений (28), (29), условиям не отрицательности (30) и обеспечивающие минимум целевой функции (27).

В рассмотренном модели транспортной задачи предполагает, что суммарные запасы поставщиков равны суммарным запросам потребителей, т. е.

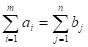
(31).

Такая задача называется задачей с правильным балансом, а ее модель? открытой.

Для того, чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей (см. равенство (31)), т. е. задача должна быть с правильным балансом.

Рассмотрим задачу:

Решение:

Введем переменные задачи (матрицы перевозок).

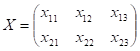
Запишем матрицу стоимостей.

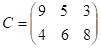
Целевая функция задачи равна сумме произведений всех соответствующих элементов матриц и :

Данная функция, определяющая суммарные затраты на все перевозки, должны достигать минимального значения.

Составим систему ограничений задачи. Сумма всех перевозок, стоящих в первой строке матрицы, должна равняться запасам первого поставщика, а сумма перевозок во второй строке матрицы — запасам второго поставщика:

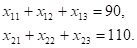
Это означает, что запасы поставщиков вывозятся полностью.

Сумма перевозок, стоящих в каждом столбце матрицы, должны быть равны запросам соответствующих потребителей:

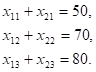
Это означает, что запросы потребителей удовлетворяются полностью. Необходимо также учитывать, что перевозки не могут быть отрицательными:

Ответ: математическая модель задачи формулируется следующим образом: найти переменные задачи, обеспечивающие минимум функции и удовлетворяющие системе ограничений.

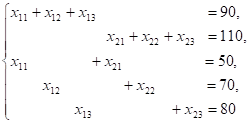
И условиям не отрицательности.