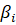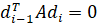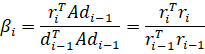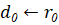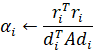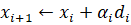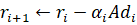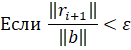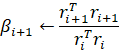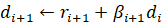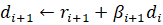Другие работы
При необходимости произвести выборку из имеющихся данных, можно воспользоваться мастером создания запросов. Этот мастер автоматически создает запросы для выборки данных из одной или нескольких таблиц. Возможность оперировать несколькими таблицами, связывая отдельные поля таблиц произвольным образом, позволяет создавать гибкие разветвленные структуры данных, удобные в управлении и эффективные…
Реферат 
Более полное погружение в придуманный мир осуществляется с помощью специального и довольно дорогого шлема-дисплея, надеваемого на голову человека. Для достижения объёмности изображения два небольших экрана, расположенные внутри шлема, создают раздельные изображения для каждого глаза. В качестве недорогого варианта погружения в мультимедиа можно использовать очки с разными стёклами…
Реферат 
База данных представляет собой структурированную совокупность данных. Эти данные могут быть любыми — от простого списка предстоящих покупок до перечня экспонатов картинной галереи или огромного количества информации в корпоративной сети. Для записи, выборки и обработки данных, хранящихся в компьютерной базе данных, необходима система управления базой данных, каковой и является ПО MySQL. Поскольку…
Реферат 
Доступность. Облака доступны всем, из любой точки, где есть Интернет, с любого компьютера, где есть браузер. Это позволяет пользователям (предприятиям) экономить на закупке высокопроизводительных, дорогостоящих компьютеров. Также сотрудники компаний становятся более мобильными так, как могут получить доступ к своему рабочему месту из любой точки земного шара, используя ноутбук, нетбук, планшетник…
Реферат 
Таким образом, для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше четырех цифр, дополнить ее слева нулями. Для перевода дробного двоичного числа (правильной дроби) в шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней правой группе окажется…
Реферат 
Коэффициенты математической модели (1.1) объекта изменяемой структуры с течением времени имеют скачки, которые можно описать на понятии гибридной функции. По определению, гибридная функция есть произведение некоторой числовой функции и функции предикат. Обозначим функцию предикат буквой L. Тогда описанием изменения коэффициента в (1.1) с учетом наличия скачков может служить выражение: В статье…
Реферат 
После успешно пройденной проверки на корректность и полноту, программа начинает производить вычисления. Программа считывает данные, заполненные в специальных полях и производит расчет по формулам. В начале выполнения программы производится проверка полноты и корректности введенных данных. Если пользовательские данные не прошли проверку — выводится соответствующее уведомление. В самом начале…
Реферат 
Грамотно разработанный интерфейс должен быть наглядным, не перегруженным визуальными элементами и в то же время обеспечивающим эффективные средства по сортировке и представлению экранных элементов. Однако удобным интерфейс делает и простая привычка. Если человек долгое время работал с одним типом интерфейса, то перейти на другой ему может быть довольно затруднительно. Именно этим фактом во многом…
Реферат 
Итак, у вас есть тема исследования, вы составили список ключевых слов, провели библиографический поиск в Интернете. У вас есть определенный результат в виде найденных книг и статей. Наверное, есть уже и некоторые полезные мысли, свои или выписанные. Более того, вы знаете, сколько времени вы потратили на эту работу, на этот результат. Мы снова будем вести хронометраж, чтобы потом оценить…
Реферат 
Важно понимать, что в случае итерационного подхода тестирование должно проводиться в рамках каждой итерации. В случае последовательных каскадных подходов тестирование должно осуществляться на каждом этапе, когда его проведение возможно. При этом в обоих случаях тестирование включает в себя множество групп тестов, которые проверяют как функциональные, так и нефункциональные аспекты деятельности И…
Реферат 
В стране под названием СССР стало модным слово «автоматизация», которое касалось буквально всех отраслей производства. Не избежала модных веяний и медицина. АСУ появились и в этой отрасли, правда, чем именно они занимались, вряд ли кто мог объяснить доходчиво. В то время ведомственной больницей МПС был приобретен уникальный вычислительный медицинский комплекс, который был разработан во Франции…
Реферат 
Модуль построения моделей бизнес-процессов в форме диаграмм потоков данных (BPM — Business Process Modeler) позволяет моделировать функционирование обследуемой организации или создаваемой ИС. В модуле BPM обеспечена возможность работы с моделями большой сложности: автоматическая перенумерация, работа с деревом процессов (включая визуальное перетаскивание ветвей), отсоединение и присоединение…
Реферат 
В это же время стало ясно, что некоторые компании и организации видят в языке UML линию стратегических интересов для своего бизнеса. Компания Rational Software вместе с несколькими организациями, изъявившими желание выделить ресурсы для разработки строгого определения версии 1.0 языка UML, учредила консорциум партнеров UML, в который первоначально вошли такие компании, как Digital Equipment…
Реферат 
Тем не менее, отсутствие указания на вредоносный характер программного кода в определении компьютерного вируса не означает, что могут быть «безвредные» вирусы. Все компьютерные вирусы следует рассматривать как вредоносные, потому что уже сам факт их распространения может нанести ущерб информационной системе. В настоящее время создано огромное количество вредоносных программ, с трудом поддающихся…
Реферат 
Скрипты могут находится в любом месте HTML-документа. Однако между строчками кода JavaScript-программы нельзя помещать теги языка HTML. Поэтому чаще всего скрипт размещают внутри раздела документа. Сама JavaScript-программа размещается между тегами … Встретив тег, браузер построчно анализирует содержимое документа до тех пор, пока не будет достигнут тег. После этого проводится проверка скрипта…
Реферат