Дискретные модели. 
Надежность программного обеспечения систем обработки данных

В дискретных моделях предполагается, что сначала проводится тестирование программного обеспечения (возможно, в несколько этапов). В случае появления отказов ищутся и исправляются все ошибки, из-за которых произошли отказы. После этого начинается период эксплуатации программного обеспечения.

МОДЕЛЬ ШУМАНА. В этой модели предполагается, что тестирование проводится в несколько этапов. Каждый этап представляет собой выполнение программы по набору тестовых данных. Выявленные в течение этапа тестирования ошибки регистрируются, но не исправляются. По завершении этапа исправляются все обнаруженные на этом этапе ошибки, корректируются тестовые наборы и проводится новый этап тестирования.

Предполагается, что при корректировке новые ошибки не вносятся, и что интенсивность обнаружения ошибок пропорциональна числу оставшихся ошибок.

Пусть всего проводятся k этапов тестирования. Обозначим продолжительность каждого этапа через t₁, …, t_k, а число ошибок, обнаруженных на каждом этапе, через m₁, …, m_k .

Пусть T = t₁ + … + t_k — общее время тестирования; n = m₁ + … + m_k — общее число обнаруженных и исправленных при тестировании ошибок; n_i = m₁ + … + m_i — число ошибок, исправленных к началу (i + 1)-го этапа тестирования (n₀ = 0).

В модели Шумана программное обеспечение на i-м этапе тестирования имеет функцию надежности:

(1.20).

.

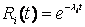
N — первоначальное количество ошибок в программном обеспечении;

N — n_i-1 — количество ошибок, оставшихся к началу i-го этапа;

C — коэффициент пропорциональности, равный:

. (1.21).

Для нахождения первоначального количества ошибок в программном обеспечении N используется уравнение:

. (1.22).

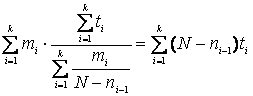
При известных значениях k; t₁, t₂, …, t_k; m₀, m₁, …, m_k из (1.21) и (1.22) можно найти значения параметров модели C и N. После чего можно определить следующие показатели:

1) число оставшихся ошибок в программном обеспечении:

; (1.23).

2) функцию надежности программного обеспечения по завершении тестирования:

(1.24).

.

Преимущества и недостатки модели. К преимуществам модели можно отнести то, что по ней можно определить все неизвестные параметры, то есть нет необходимости обращаться к другим моделям, что сокращает время расчета надежности.

К недостаткам относится предположение, что при корректировке не вносятся новые ошибки, а это не всегда имеет место в реальных программах. Кроме того, в процессе тестирования необходимо регистрировать большое количество данных, необходимых для расчета по формулам этой модели.

Пример расчета. Длительности этапов тестирования составляют часов, часов, часов. Число отказов на первом этапе, на втором —, на третьем —. Необходимо определить число оставшихся ошибок в программном обеспечении, а также функцию надежности программного обеспечения по завершении тестирования.

Методом подбора из уравнения (1.22) найдем, что первоначальное количество ошибок .

Найдем число оставшихся ошибок в программном обеспечении по (1.23):

.

По формуле (1.21) найдем значение параметра C:

.

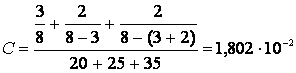
Тогда:

.

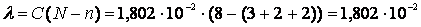
Подставляя l в (1.24), получим функцию надежности программного обеспечения по завершении тестирования:

.

МОДЕЛЬ МУСА. В этой модели надежность программного обеспечения на этапе эксплуатации оценивается по результатам тестирования.

Пусть T — суммарное время тестирования, n — число отказов, произошедших за время тестирования.

Тогда по модели Муса средняя наработка до отказа после тестирования на этапе эксплуатации определяется по формуле:

(1.25).

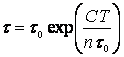
где t₀ — средняя наработка до отказа до начала тестирования, C — коэффициент, учитывающий уплотнение тестового времени по сравнению с временем реальной эксплуатации. Например, если один час тестирования соответствует 12 ч работы в реальных условиях, то C = 12.

Неизвестный параметр t₀ можно оценить из следующего соотношения:

(1.26).

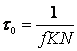
где N — первоначальное число ошибок в программном обеспечении. Его можно оценить с помощью другой модели, позволяющей определить N на основе статистических данных, полученных при тестировании;

K — коэффициент проявления ошибок. Значение K определяется эмпирическим путем по однотипным программам. Обычно это значение изменяется от 1,5Ч10^-7 до 4Ч10^-7;

f — средняя скорость выполнения одного оператора программы, равная отношению средней скорости исполнения программного обеспечения (A) к числу команд (операторов) (B).

Надежность программного обеспечения для периода эксплуатации t определяется по формуле:

. (1.27).

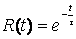
Преимущества и недостатки модели. К преимуществам модели можно отнести то, что нет необходимости фиксировать моменты отказов. В случае появления отказов ошибки регистрируются, а исправляются лишь по завершении этапа тестирования.

К недостаткам модели относится то, что для определения первоначального числа ошибок в программном обеспечении необходимо вести расчеты по другой модели, что приводит к дополнительным затратам времени.

Пример расчета. Длительности этапов тестирования составляют часов, часов, часов. Число отказов на первом этапе, на втором —, на третьем —. Средняя скорость исполнения программного обеспечения операторов/час, количество операторов в ПО. Определить надежность программного обеспечения для периода эксплуатации часов.

Найдем среднюю скорость выполнения одного оператора:

(час^-1).

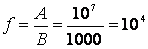
Первоначальное количество ошибок в программном обеспечении N найдем по модели Шумана методом подбора из уравнения (1.22): наименьшее различие значений правой и левой частей этого уравнения достигается при. Следовательно, это и есть первоначальное количество ошибок в программном обеспечении.

Коэффициент проявления ошибок K примем равным .

Найдем значение параметра t₀ по (1.26):

часа.

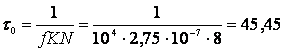
Примем значение коэффициента .

Тогда средняя наработка до отказа после тестирования на этапе эксплуатации по (1.25):

часов.

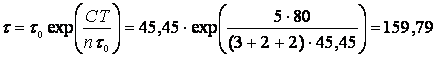
Найдем надежность программного обеспечения для периода эксплуатации часов по формуле (1.27):

.