Непрерывные динамические модели

Пусть функционирование программного обеспечения описывается графом состояний, изображенным на рисунке 1.3. Здесь S_i — состояние системы, когда произошел i-й по счету отказ, l_i — интенсивность наступления следующего ((i + 1)-го по счету) отказа.

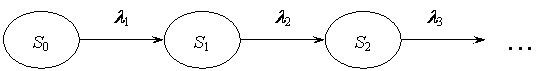
Рис. 1.3. Граф состояний функционирования программного обеспечения

Можно задать какую-либо зависимость интенсивности наступления следующего отказа от числа уже наступивших отказов, например,.

l_i= l₀rⁱ,.

где r<1. Значения l₀ и r можно оценить статистически по данным о моментах отказов.

Поясним процессы, происходящие в ходе отказов и восстановлений ПО. Если принять l_i как случайную величину с функцией распределения l (t), то эта функция — монотонно убывающая [7], так как во времени интенсивность отказов уменьшается. После исправления мгновенная интенсивность отказов резко уменьшается скачком (точки 1 и 2 на рис. 1.4).

Рис. 1.4. График зависимости интенсивности отказов от времени

Рассмотрим модели, по которым можно производить расчеты показателей надежности.

Модель джелински-моранды [7]. Модель основана на допущениях, что время до следующего отказа распределено экспоненциально, а интенсивность отказов программы пропорциональна количеству оставшихся в программе ошибок.

Согласно этим допущениям вероятность безотказной работы ПО как функция времени t_i равна:

(1.1).

где интенсивность отказов:

. (1.2).

Здесь C_D — коэффициент пропорциональности;

N — первоначальное количество ошибок.

В (1.1) отсчет времени начинается от момента последнего (i — 1)-го отказа программы.

По методу максимума правдоподобия на основании (1.1), обозначая через k номер прогнозируемого отказа, получим, что функция правдоподобия имеет вид:

. (1.3).

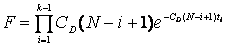
Логарифмическая функция правдоподобия имеет вид:

. (1.4).

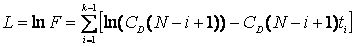
Отсюда условия для нахождения экстремума:

(1.5).

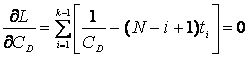
. (1.6).

Из (1.6) получим:

. (1.7).

Подставим (1.7) в (1.5). Получим:

. (1.8).

При известных значениях k; t₁, t₂, …, t_k из (1.7) и (1.8) можно найти значения параметров модели C_D и N, а затем интенсивность отказов, время от последнего до следующего отказа t_k+1, вероятность безотказной работы через время t_k+1 после последнего отказа.

Преимущества и недостатки модели. Основным преимуществом модели является простота расчетов. Недостаток этой модели состоит в том, что при неточном определении величины N интенсивность отказов программы может стать отрицательной, что приводит к бессмысленному результату. Кроме того, предполагается, что при исправлении обнаруженных ошибок не вносятся новые ошибки, что тоже не всегда выполняется.

Пример расчета. Пусть в ходе отладки зафиксированы интервалы времени t₁=10, t₂=20, t₃=25 часов между отказами программы. Необходимо определить вероятность:

.

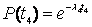
отсутствия следующего (четвертого) отказа.

Первоначальное количество ошибок N находим методом подбора. Если N=3, то есть обнаружены все ошибки, то в левой части (1.8) имеем:

;

а в правой части:

.

Если N=4, левая и правая части соответственно равны 152 и 150. Если N=5, соответственно 210 и 205.

Следовательно, наименьшую ошибку при решении (1.8) обеспечит N=4, откуда по формуле (1.7):

.

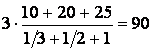
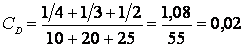
Из (1.2) получаем.

.

Следовательно, среднее время до следующего отказа составляет:

часов.

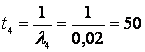
Тогда, подставляя найденные значения l₄ и t₄ в (1.1), получим вероятность отсутствия четвертого отказа:

.

Модель переходных вероятностей Маркова [3]. Модель позволяет получить оценки и предсказания вероятного числа ошибок, которые будут исправлены в заданное время, на основе предварительного моделирования интенсивности случающихся ошибок l, а также принятой системы исправления ошибок, работающей с интенсивностью m. Модель позволяет получить предсказания для готовности A (t) и надежности R (t) системы ПО.

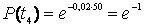
Принимаются следующие основные ограничения разрабатываемой модели:

• — любая ошибка рассматривается как случайная и без градации последствий, которые она порождает;
• — интенсивность проявления ошибок постоянна и равна l;
• — интенсивность исправления ошибок постоянна и равна m;

время перехода системы из одного состояния в другое бесконечно мало.

Рассмотрим систему, начинающую работу в момент времени t = 0. Система работает до появления ошибки в соответствии с предопределенным критерием. Результаты эксперимента собираются в отрезки времени, за которые могут произойти отказы в работе. Тогда переменная времени случайного сбоя может быть определена как:

(1.9).

где — местоположение точек на дискретной временной оси эксперимента. Предположим, что случайная переменная имеет функцию распределения:

(1.10).

и, если она существует, то плотность функции распределения будет:

. (1.11).

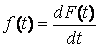
Надежность системы R (t) определяется вероятностью отсутствия сбоя в интервале [0, t]:

. (1.12).

Под готовностью системы к моменту времени t понимается вероятность того, что система находится в рабочем состоянии во время t:

. (1.13).

Предположим, что в начальный период (t = 0) система содержит неизвестное число (п) ошибок. В качестве начала отсчета времени работы системы выбирается начало фазы тестирования. Принимаем также, что процессы обнаружения и исправления ошибок реализуются попеременно и последовательно.

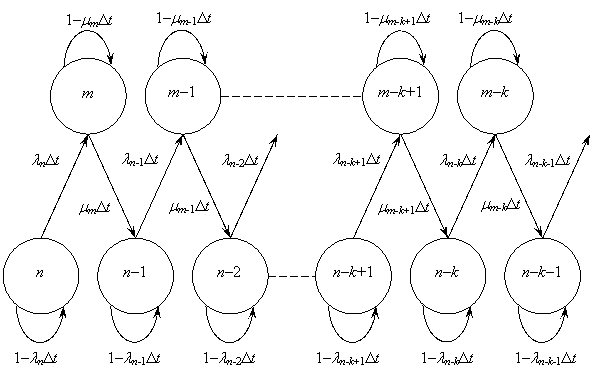
Рис. 1.5. Модель многих состояний для оценки характеристик ПО

Ряд состояний системы {n, п — 1, п — 2, …} соответствует процессам обнаружения ошибок. По аналогии для случая устранения ошибок введем состояния системы {т, т — 1, т — 2, …}. Система находится в состоянии (п — k), если ошибка (k — 1) уже исправлена, а ошибка k еще не обнаружена. В то же время система будет находиться в состоянии (т — k) после того, как ошибка k обнаружена, но еще не исправлена. Общая схема модели с указанием вероятностей перехода между состояниями показана на рис. 1.5.

Пусть S'(t) есть случайная переменная, через которую обозначено состояние системы в момент времени t. Эксперимент будет построен так, что в некоторый момент времени предполагаем систему остановленной и наблюдаем ее состояние. Пространство возможных состояний S системы может быть представлено так:

.

Теперь предположим, что в моменты (любая последовательность наблюдений) последовательность случайных переменных удовлетворяет для любого положительного целого числа l следующему равенству:

(1.14).

где соответствуют последовательности состояний.

Таким образом, любое состояние модели определяется рядом переходных вероятностей {P_ij}, где P_ij обозначает вероятность перехода из состояния i в состояние j и не зависит от предшествующих и последующих состояний системы, кроме состояний i и j. Вероятность перехода из состояния (п — k) к состоянию (т — k) равна при k = 0, 1, 2, … Аналогично этому вероятность перехода из состояния (т — k) к состоянию (п — k — 1) равна при k = 0, 1, 2, …

Интенсивности перехода l_j и m_j зависят от текущего состояния системы. Для системы ПО l_j означает интенсивность возникновения (проявления), a m_j — интенсивность устранения ошибок. Следовательно, полная матрица переходных вероятностей системы может быть представлена следующим образом:

(1.15).

Далее получим выражения для готовности A (t) и надежности R (t) системы в терминах вероятности состояния занятости системы:

(1.16).

(1.17).

Выражение для готовности системы во время t (tі0) получим на основе ее определения:

(1.18).

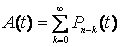
Готовность системы во время t определяется как результат простого сложения всех вероятностей состояний занятости.

Надежность системы зависит от степени ее отладки, т. е. чем выше степень отладки системы, тем больше ожидаемая надежность. Предположим, что к моменту t система только что вошла в состояние (n — k), т. е. ошибка k только что устранена. Назовем это время как t. Тогда в интервале времени (0, T_k+1), где t = T_k+1 может проявиться ошибка (k + 1) при принятой постоянной интенсивности проявления ошибок l_k .

На основании формулы функции надежности, порождающей вероятность отсутствия сбоев в интервале времени от 0 до t,.

.

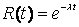
получим выражение для надежности:

(1.19).

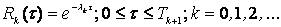
Преимущества и недостатки модели. Достоинство модели состоит в том, что рассматривается достаточно большая система ПО, насчитывающая около 10⁵ кодов, что позволяет надеяться на значимость статистических выводов.

К недостаткам модели относится то, что она предсказывает поведение системы во время функционирования в среднем. На практике интенсивность исправления ошибок запаздывает по отношению к их обнаружению, что в известной мере затрудняет процесс.

Предполагается, что модель в начальный период будет использоваться со значениями l и m, которые были получены на базе накопления прошлого опыта. В связи с тем, что последующая работа модели позволит в свою очередь накопить данные об ошибках, возможно дальнейшее повышение точности анализа, используя данные предыдущего моделирования.

Пример расчета. Пусть в ходе отладки зафиксированы интервалы времени t₁=10, t₂=20, t₃=25 часов между отказами программы. Система находится в состоянии, когда ошибка 3 уже исправлена, а ошибка 4 еще не обнаружена. Необходимо определить вероятность:

.

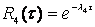
отсутствия следующего (четвертого) отказа.

Здесь часов — это время, когда последняя обнаруженная ошибка исправлена.

Величину l_i определим по модели Джелински-Моранды (формула (1.2)):

.

Значения C_D и N определим по формулам (1.7) и (1.8).

Первоначальное количество ошибок N находим методом подбора. Если N=3, то есть обнаружены все ошибки, то в левой части (1.8) имеем:

;

а в правой части:

.

Если N=4, левая и правая части соответственно равны 152 и 150. Если N=5, соответственно 210 и 205.

Следовательно, наименьшую ошибку при решении (1.8) обеспечит N=4, откуда по формуле (1.7):

.

Из (1.2) получаем:

.

Тогда, подставляя найденное значение l₄ в (1.19), получим вероятность отсутствия четвертого отказа:

.