Аналитический обзор и постановка задачи

В данном разделе производится обзор существующих методов и по итогам ставится задача исследования.

В первом параграфе этого раздела описаны основные понятия теории сетей. Приводятся их необходимые описания и определения.

Во втором параграфе производится обзор существующих графовых моделей, вводятся понятия случайных графов Барабаши-Альберт, Эрдеша-Реньи, Уаттса-Строгатца, описаны правила их генерации.

В третьем параграфе вводится понятие случайного графа с нелинейным правилом предпочтительного связывания (НППС), который был предложен Задорожным В. Н. в 2010 году.

В четвёртом параграфе обсуждаются алгоритмы ускоренной генерации графов с НППС, калибровки графовых моделей для реализации заданного коэффициента кластеризации.

В конце раздела, исходя из представленной информации, ставится задача данного исследования.

1.1 Структурные характеристики случайных графов

В математической теории графов граф — это совокупность непустого множества вершин и набор пар вершин (связей между вершинами).

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах [1].

Степень связности одной вершины равна количеству рёбер присоединённых к этой вершине. Также часто используется понятие средней степени связности графа. Данное значение можно получить, если поделить число рёбер в графе на число вершин это же графа и умножить на два, поскольку одно ребро связывает два узла.

Большие сети — это сети, содержащие тысячи вершин и связей между ними.

Случайные графы — это графы, которые генерируются в результате некоторого случайного процесса. Случайные графы (сл.г.) имеют ряд важных характеристик. Этими характеристиками обладают как реальные сети, так и их модели. Эти характеристики характеризуют важные свойства сетей, также по ним можно судить насколько точной является та или иная графовая модель сети.

Рассмотрим первую характеристику — диаметр графа. Диаметр графа определяет максимальное расстояние (измеряемое в числе ребер) между вершинами в неориентированном графе, полученное в результате анализа расстояний между всеми парами вершин. С понятием диаметра графа связан эффект «Тесного мира», также известный, как правило «шести рукопожатий». Это правило означает, что перебирая круг своих ближайших знакомых, затем людей, знающих наших ближайших знакомых и т. д. любой человек опосредовано знаком с любым другим человеком в мире. Причём, как правило, число элементов в цепи не превышает 6.

Другой, не менее важной характеристикой графа является коэффициент кластеризации. Коэффициент кластеризации C в общем случае определяется как утроенное отношение среднего числа n «треугольников» (три вершины, связанные тремя рёбрами) в графе к среднему числу nV «вилок» (число путей длины 2).

Калибровка графа позволяет построить модель графа так, чтобы сохранить распределение степени связности (РСС) вершин, путём подбора других параметров, в зависимости от поставленных целей.

Некоторые модели случайных графов

В данной главе рассматриваются три основных модели случайных графов.

Первая модель была предложена в 1999 г. Альбертом Барабаши и Реки Альберт, которые независимо открыли процесс предпочтительного присоединения.

Другой рассмотренной моделью является модель Дункана Уаттса и Стивена Строгатца предложенная ими в 1998 г. Ими был обнаружен эффект, названный «тесным миром» .

Третьей описанной моделью является модель Эрдеша-Реньи для генерации случайных графов. Она была предложена на рубеже 50-х и 60-х годов.

Модель графа Барабаши — Альберт

Модель графа Барабаши — Альберт (граф БА) представляет собой алгоритм генерации случайных безмасштабных сетей с использованием правила предпочтительного связывания (ПС).

Правило предпочтительного связывания говорит, что чем большую степень связности имеет вершина, тем выше вероятность присоединения к ней новых вершин. Если для присоединения выбирать вершину случайным образом, то вероятность выбора определённой вершины будет пропорциональна её степени связности. Данное правило соответствует принципу «богатый становится богаче» .

Данный граф выращивается из небольшого графа-затравки, у которого степень связности каждой вершины должны быть не меньше единицы.

Каждая новая вершина присоединяется к уже существующим вершинам с вероятностью пропорциональной степени связности этих вершин. Вероятность pi того, что вершина присоединится к i-ой вершине равна:

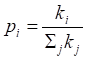
(1).

где ki -степень i-ой вершины [2].

Модель графа Уаттса — Строгатца

Большинство моделей сложных сетей представляют собой численную реализацию графа и генерируются на компьютере. Данная же модель появилась задолго до свободного распространения вычислительной техники.

Д. Уаттс и С. Строгатц обнаружили феномен, характерный для многих реальных сетей, названный эффектом «тесного мира» .

Модель «тесного мира» состоит в том, что перебирая круг своих ближайших знакомых, затем людей, знающих наших ближайших знакомых (но не знающих нас непосредственно), и т. д. легко убедиться в следующем: достаточно проследить за небольшим числом цепочек таких знакомств, чтобы понять, что любой из нас опосредовано знаком с любым членом общества. В этом смысле наш мир является тесным, откуда и пошло название этой модели [3].

Сетевые структуры, соответствующие свойствам малых миров, обладают следующими типичными свойствами: малая средняя длина пути относительно диаметра сети (что характерно также для случайных сетей) и большой коэффициент кластеризации.

При исследовании этого феномена ими была предложена процедура построения наглядной модели сети, которой присущ этот феномен.

Чтобы построить сеть «тесного мира», следует начать с регулярной циклической решётки с N вершинами, каждая из которых соединена с k ближайшими соседями в каждом направлении. Для каждой вершины задаётся 2k связей, где N «log2 (N) «1. Затем каждое ребро пересоединяется со случайной парой вершин с вероятностью p.

При условии p = 0 получается упорядоченная решётка с большим количеством циклов и большими расстояниями, а при условии p > 1 сеть становится случайным графом с короткими расстояниями, и малым количеством циклов.

Данная сеть может иметь три состояния:

• ? регулярная сеть, каждый узел которой соединён с четырьмя соседними;
• ? та же сеть, у которой некоторые «ближние» связи случайным образом заменены более «дальними» (именно в этом случае возникает феномен «тесного мира»);
• ? случайная сеть, в которой количество подобных замен превысило некоторый установленный порог [4].

На рисунке 1 представлена иллюстрация данной модели.

Рисунок 1 — Модель графа Уаттса-Строгатса [4].

Параметр p в данной модели отвечает за переброс рёбер в случайные положения. Так по рисунку 1 можно увидеть трансформацию из регулярной цепочки в модель «тесного мира», а затем в случайный граф.

Компьютерная модель «малого мира» была разработана Уаттсом и Строгатсом несколькими годами позже.

Модель Уаттса-Строгатса представляет собой модель генерации случайного графа, имеющего высокий коэффициент кластеризации вершин [3] и относительно небольшую среднюю длину пути.

Модель графа Эрдеша-Реньи

В теории графов модель Эрдеша — Реньи представляет собой модель для генерации случайного графа с постоянной вероятностью появления ребра между двумя вершинами независимо от других ребер. Согласно данной модели, граф конструируется с помощью соединения пар вершин случайным образом. Каждое ребро включается в граф с вероятностью p независимо для каждой пары вершин. С ростом p от 0 до 1 граф становится все более насыщенным ребрами. При p = 0 имеем пустой граф (граф, не имеющий ребер), при p = 1 — полносвязный граф. При фиксированном количестве вершин в графе вероятность p — единственный входной параметр модели Эрдеша — Реньи.

Простота модели Эрдеша — Реньи случайного графа позволяет получать различные аналитические оценки. Однако стоит отметить, что модель в среднем не воспроизводит такие типичные свойства реальных сетей, как степень вершин, величина коэффициента кластеризации и длины пути. [5].

Модель графа с НППС

Случайные графы с НППС были впервые предложены В. Н. Задорожным в 2010 году в статье [6]. Данные графы генерируются на основе правила «предпочтительного связывания» («богатый становится богаче»). Граф с НППС выращивается из графа-затравки итерационно, путём добавления вершин со случайным числом рёбер r, с заданной функцией предпочтения f ?0, зависящей от степени связности ki вершины. Вероятность pi присоединения свободным концом нового ребра к уже существующей вершине графа зависит от функции предпочтения и вычисляется по формуле (2):

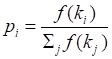
. (2).

Модели графов с НППС в последнее время получили широкое развитие. В работе [7] были найдены эффективные способы генерации графа. В [6, 8] представлены такие способы калибровки графов, которые позволяют при заданном распределении вероятностей r, путём подбора функции предпочтения f(k) генерировать граф с требуемым распределением степени связности вершин.

Но, не смотря на точное совпадение средней степени связности графа, данная модель во многих случаях не может обеспечить достаточно точное совпадение всех остальных структурных характеристик.

1.2 Обзор аналогов

В данном разделе производится небольшой обзор существующих алгоритмов построения графовых моделей и их калибровки.

Рассматриваются алгоритм генерации графа БА и ускоренный метод генерации графа с НППС, а также метод сепарабельной реконфигурации. Представляются графики распределения степени связности графов. Описываются результаты сравнений различных характеристик реальных сетей и графовых моделей.

Ускоренный метод генерации графа БА и графа с НППС

Алгоритм данного метода был представлен в [9].

Граф БА генерируется из небольшого графа-затравки путём добавления новых вершин с фиксированным числом рёбер m? 1. Свободный конец нового ребра присоединяется в соответствии с формулой (3):

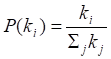
j = 1,…, N, (3).

где N — текущее число вершин в графе.

Из формулы видно, что чем больше степень связности у вершины, тем выше вероятность её выбора.

На рисунке 2 представлена блок схема этого алгоритма.

Рисунок 2 — Схема программы генерации графа БА [9].

Выбор вершин для присоединения может быть выполнен на основе стандартного подхода разыгрывания дискретной случайной величины (ДСВ). Данный подход можно описать так. Пусть задана некоторая система непересекающихся событий {А 1, …, Аn}, заключающихся в выборе очередной вершины (всего в графе n вершин). Вероятности выбора вершин события {А 1, …, Аn} равны соответственно p1, …, pn, (p1 + p2 + … + pn = 1). При построении алгоритма отрезок [0,1) необходимо разбить на n интервалов длиной p1, …, pn, и отслеживать попадание сгенерированного значения большой случайной величины (БСВ) z в соответствующий интервал. Программная реализация данного алгоритма в [10] была названа БА_ДСВ (m, N, G).

В генератор БА_ДСВ (m, N, G) передаётся параметр m, определяющий число рёбер, добавляемых на каждом шаге, и число вершин N в генерируемом графе. При генерации передаётся также граф-затравка G, содержащий M вершин (M? N).

На каждом шаге генерации добавляется новая вершина vi (M? i < N) c m рёбрами. Добавления m рёбер являются независимыми событиями, поэтому каждая следующая выбранная для присоединения вершина добавляется в специальный список lst, пока не будут выбраны все m вершин. После выбора всех m вершин (выход из цикла) в граф G «одновременно» добавляются m новых рёбер e = (vi, vlst[h]), между добавленной вершиной vi и вершинами из списка vlst[h] (p = 1, …, m). Далее список lst очищается, и алгоритм переходит к очередному шагу добавления новой вершины, пока не будут добавлены все (N — M) вершин.

Основная трудоёмкость рассмотренного алгоритма заключается в количестве итераций при выборе вершины для присоединения, поскольку в исследуемых сетях таких вершин сотни тысяч. Среднее число итераций при выборе вершин в графе, содержащем n вершин при условии, что степени вершин при их переборе распределены случайно, равно n / 2 [10].

Данный алгоритм можно ускорить, если разбить всё его множество вершин на отдельные слои. Слой — это подмножество вершин, которые имеют одинаковую степень связности.

После того, как всё множество вершин разбито на слои, происходит выбор новой вершины для присоединения. Сначала случайным образом выбирается номер слоя, а затем из этого слоя равновероятно выбирается вершина.

Схема данного алгоритма представлена на рисунке 3.

Рисунок 3 — Схема программы ускоренного метода генерации графа БА и графа с НППС [10].

Основная трудоёмкость данного алгоритма заключается в количестве итераций, которые необходимо выполнить для выбора слоя вершин. Количество итераций зависит от числа вершин в графе: чем больше граф, тем труднее выполнить данный алгоритм.

Генерация графа БА размером 100 тыс. вершин базовым алгоритмом занимает около трёх часов.

На рисунке 4 представлены графики распределения степени связности графов, выращенных на калиброванных генераторах. Эти степени хорошо согласуются с эмпирическими вероятностями степеней. Данные генераторы можно рассматривать и как результаты идентификации сетей предпочтительного связывания.

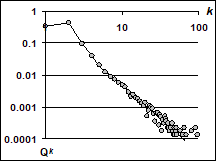
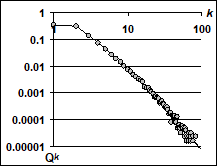
Рисунок 4 — РСС (слева на право: РСС калиброванного графа и сети автономных систем интернет; РСС калиброванного графа и сети маршрутизаторов интернет; РСС калиброванного графа и сети участия актёров в общих фильмах) [6].

Первый график на рисунке 4 характеризует качество идентификации сети автономных систем интернет по данным [11] (число узлов и рёбер равны соответственно N = 22 963, R = 48 436).

Второй график на данном рисунке характеризует качество идентификации сети маршрутизаторов интернет по данным [12] (N = 124 651, R = 207 214). Параметры генератора:, ,, ,, .

Последний график характеризует идентификацию сети участия актеров в общих фильмах [13] (N = 511 416 — без изолированных узлов, R = 1 463 331). Два соответствующих актерам узла связаны ребром, если эти актеры снимались в одном фильме. Здесь, численно фиксированы, и при k > 10 общая формула весов имеет вид .

Однако соответствие по РСС сети и ее модели не означает, что эти структуры соответствуют по другим структурным характеристикам, а модель является адекватной. Так на IV региональной научно-практической конференции был представлен доклад [14], в котором особое внимание уделялось исследованию диаметра сл.г. В данной работе был проведён следующий эксперимент. Было выбрано 7 реальных сетей с уже известными параметрами. Для каждой из этих сетей было построено несколько различных модели сл.г. и подсчитан диаметр, как реальной сети, так и моделей. Длина выборки равнялась 10. Результаты этого эксперимента представлены в таблице 1.

Таблица 1 — Сравнение диаметра у реальных сетей и их моделей.

Из этой таблицы видно, что среднее значение диаметра графа БА практически совпадает только в двух случаях, в двух других случаях диаметр графа БА меньше диаметра реальной сети почти в два раза. В модели графа Эрдеша-Реньи для сети автономных систем диаметр модели меньше почти в четыре раза. Диаметр графа в моделях Уаттса-Строгантца при p = 0 имеет чрезмерно большое значение и совершенно не соответствует диаметру реальных сетей. Что касается графа с НППС, то тут значения диаметра в целом получаются значительно меньше.

Таким образом, из таблицы 1 можно сделать вывод, что ни одна из моделей не соответствует реальным сетям по такой важной характеристики как диаметр графа.

В работе [15] производится исследование соответствия графовых моделей и их сетей на количество подграфов в виде квадрата. Квадратом назван подграф из четырёх вершин и четырёх рёбер, связанных в кольцо.

Данные, полученные в [15], показывают, что при одинаковом числе узлов N и ребер E, число квадратов в графах БА, конфигурационных графах, графах с НППС оказывается значительно меньше, чем в реальных сетях. Эти данные представлены ниже в таблице 2.

Конфигурационная модель генерации графа БА описана в [3]. Её можно представить следующим образом.

Пусть дано распределение Pk степени связности N вершин.

• 1. Помечаем степенями связности ki все N вершин Map <vi, ki> (i = 1, N).
• 2. Рисуем «хвосты рёбер» в соответствии с полученными числами ki.
• 3. Распределяем «хвосты ребер» на пары случайно равновероятно, формируя ребра между вершинами.

Таблица 2 — Число квадратов в реальных сетях (n?реал), в графе БА (nграфБА), в конфигурационной модели (nконф.м.), в графе с НППС (nграфНППС).

Из таблицы 2 видно, что модель графа БА содержит наименьшее число квадратов и наиболее сильно отличается от числа квадратов в реальных сетях. Число квадратов в конфигурационной модели в разы больше, но всё же достаточно. Наибольшим числом квадратов обладает граф с НППС, однако их всё равно на порядки меньше, чем в реальных сетях.

С помощью программы предложенной в [16] нетрудно рассчитать значения коэффициента кластеризации в сетях и их графовых моделях. Так в таблице 3 приводятся данные расчёта коэффициента кластеризации сети автономных систем интернет и её моделей. Графа БА сгенерирован с параметром средней степени связности m = 2. Граф с НППС был откалиброванным по заданному эмпирическому РСС. Количество вершин в данных моделях случайных графов соответствует числу узлов в реальной сети автономных систем: 22 963 узла.

Таблица 3 — Расчеты коэффициента кластеризации в различных сетях.

Из таблицы 3 можно увидеть, что значение коэффициента кластеризации в модели графа БА отличается от значения коэффициента кластеризации в реальной сети на несколько порядков. Граф, сгенерированный в соответствии с НППС, имеет намного большее значение коэффициента кластеризации. Однако, несмотря на то, что значение параметра значительно увеличилось, оно всё равно отличается от значения этого же параметра в реальной сети более чем в два раза.

В работе [10] приведены данные об исследовании других реальных сетей и сравнении их с моделью графа БА по коэффициенту кластеризации. Также было установлено, что в реальных сетях эта структурная характеристика на порядок больше её показателя в графах БА. Результаты данного исследования представлены в таблице 4.

Таблица 4 — Коэффициент кластеризации в реальных сетях (С?реал) и в графе БА (С?графБАтеор) [10].

По таблице 4 видно, что хотя модель графа БА выращивалась для того же количества вершин N и с тем же параметром средней степени связности m значения коэффициента кластеризации в графе БА в некоторых случаях меньше на несколько порядков.

Метод сепарабельной реконфигурации по коэффициенту кластеризации

В исследовании [10] для решения проблемы заниженного коэффициента кластеризации в графовых моделях сетей предлагается алгоритм сепарабельной реконфигурации по коэффициенту кластеризации. Сепарабельной реконфигурацией называется такое изменение структуры графа путём перераспределения рёбер, при котором не изменяется РСС вершин. Данный метод предполагает увеличение числа «треугольников» в графе. Иллюстрация этого алгоритма представлена на рисунке 5.

Рисунок 5 — Иллюстрация метода сепарабельной реконфигурации [10].

Для увеличения числа «треугольников» в графе циклически необходимое число раз используется следующая процедура.

• 1. Случайно выбираем ребро R, не входящее в треугольник. Определяем степени связности l и m вершин, инцидентных R.
• 2. Случайно выбираем вершину a и среди смежных ей вершин отыскиваем две несвязные вершины b и c. Если таких нет, возвращаемся к 2.
• 3. Определяем степени связности i и j вершин b и c соответственно. Ребро R переносим — ставим его между найденными вершинами b и c. В результате этой операции количество вершин со степенями связности l, m, i, j уменьшается, а количество вершин со степенями l — 1, m — 1, i + 1, j + 1 увеличивается (вследствие чего изменяется РСС).
• 4. Компенсируем изменение РСС:
  • ? выбираем случайное ребро (отличное от R) со степенями связности i + 1, j + 1;
  • ? находим случайные вершины со степенями связности l — 1, m — 1;
  • ? перенося выбранное ребро, соединяем найденные вершины [9].

Данный метод позволяет изменять коэффициент кластеризации, сохраняя РСС. Одним из недостатков данного метода является то, что необходимо хранить ссылки на слои вершин в специальной структуре данных. На основе этого метода был разработан новый алгоритм, представленный в этой работе.

Предложенный метод [10] реконфигурации графа позволяет изменять его коэффициент кластеризации на несколько порядков и при этом сохранять его РСС.

Иллюстрация работы этого метода представлена на рисунке 6.

Рисунок 6 — Иллюстрация метода сепарабельной реконфигурации [10]

На рисунке 6а представлен граф БА, а на рисунке 6б представлен этот же граф БА, но уже после сепарабельной реконфигурации.

Выводы по главе и постановка задачи ВКР

Во время анализа предметной области было выявлено следующее.

• 1. Модель классического случайного графа (графа Эрдеша-Реньи) плохо воспроизводит некоторые свойства реальных сетей (степени вершин, величину коэффициента кластеризации и длины пути).
• 2. В 1999 году был предложен случайный граф Барабаши-Альберт (граф БА). Графы БА по своим структурным свойствам оказались более адекватными моделями реальных сетей, чем графы Эрдеша-Реньи.
• 3. Эффект «тесного мира» был обнаружен при исследовании реальных сетей и характеризует собой «правило шести рукопожатий» т. е. перебирая круг своих ближайших знакомых, затем людей, знающих наших ближайших знакомых и т. д. любой человек опосредовано знаком с любым другим человеком в мире. Причём, как правило, число элементов в цепи не превышает 6.
• 4. Графы БА имеют небольшую среднюю длину пути между вершинами и таким образом также демонстрируют собой эффект «тесного мира» .
• 5. В 2010 модель графа БА было обобщена в виде модели графов с НППС.
• 6. Графы с НППС позволяют генерировать графовые модели с заданным РСС вершин, путём подбора нужной функции предпочтения.
• 7. Существующие модели сл.г. обычно имеют значительное отличие от реальных сетей по диаметру и частоте появления подграфов.
• 8. Как правило, для графов НППС коэффициенты кластеризации в среднем меньше коэффициентов кластеризации в реальной сети.
• 9. Единственным методом калибровки графов по коэффициенту кластеризации является метод сепарабельной реконфигурации графа, но этот метод нарушает структуру, сформированную в результате применения графа с НППС.
• 10. При генерации графов с НППС конкретно не оговаривается, с какой вершиной нужно соединять новое ребро. Различные способы выбора данной вершины позволяют изменять структурные характеристики графа.

Таким образом, можно сформулировать задачи, которые необходимо выполнить в данной работе.

• 1. Разработка нового ускоренного алгоритма калибровки по коэффициенту кластеризации.
• 2. Программная реализация полученного алгоритма в системе моделирования Simbigraph.