Простейшие методы сортировки: метод обмена
Данный метод относится к классу простейших, занимая в нем последнее место по производительности. Тем не менее, он очень широко известен, видимо, благодаря своему одному легко запоминающемуся названию — метод всплывающего пузырька (или тонущего шарика, если кому-то так больше нравится). Работа алгоритма действительно похожа на всплывание наверх пузырьков воздуха: сначала на самый верх всплывает… Читать ещё >
Простейшие методы сортировки: метод обмена (реферат, курсовая, диплом, контрольная)
Данный метод относится к классу простейших, занимая в нем последнее место по производительности. Тем не менее, он очень широко известен, видимо, благодаря своему одному легко запоминающемуся названию — метод всплывающего пузырька (или тонущего шарика, если кому-то так больше нравится). Работа алгоритма действительно похожа на всплывание наверх пузырьков воздуха: сначала на самый верх всплывает самый легкий элемент, потом за ним — чуть более тяжелый и т. д.
Пусть имеется n элементов, а 1 а 2, а 3,…, аn, расположенных в ячейках массива. Для простоты будем считать, что сам элемент совпадает с его ключом. Алгоритм состоит в повторении n-1 шага, на каждом из которых в оставшемся необработанном наборе за счет попарного сравнения соседних элементов отыскивается минимальный элемент.
Шаг 1. Сравниваем аn с аn-1 и если аn < аn-1 то меняем их местами, потом сравниваем аn-1 с аn-2 и, возможно, переставляем их, сравниваем аn-2 и аn-3 и т. д. до сравнения и, возможно, перестановки, а 2 и, а 1. В результате на первом месте в массиве оказывается самый минимальный элемент, который в дальнейшей сортировке не участвует Шаг 2. Аналогично сравниваем аn с аn-1, аn-1 с аn-2 и т. д., а 3 с, а 2, в результате чего на месте, а 2 оказывается второй наименьший элемент, который вместе с, а 1 образует начальную часть упорядоченного массива Шаг 3. Аналогичными сравнениями и перестановками среди элементов, а 3, а 4, …, аn находится наименьший, который занимает место, а 3 …
Шаг n-1. К этому моменту первые n-2 элемента в массиве уже упорядочены и остается «навести порядок» только между двумя последними элементами аn-1 и аn. На этом сортировка заканчивается.
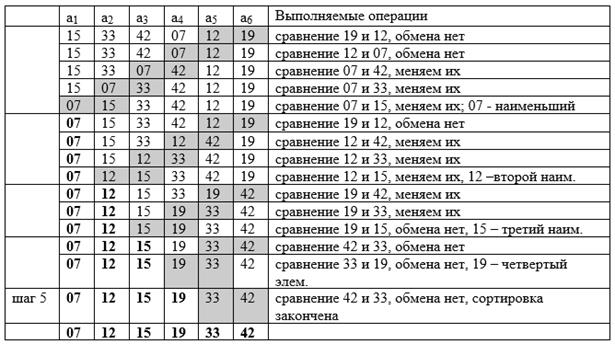
Пример. Дано 6 элементов — целые числа 15, 33, 42, 07, 12, 19.
Итого, для шести элементов сделано 5+4+3+2+1 = 15 сравнений и 8 перестановок.
В общем случае, на каждом из n-1 шагов выполняется в среднем n/2 сравнений, поэтому оценка для числа сравнений выражается соотношением n (n-1)/2, т. е. данный метод относится к классу O (n2). Аналогично, число перестановок тоже пропорционально n2. Несмотря на то, что было предложено несколько улучшений данного метода (есть очень красивые названия — например, шейкер-сортировка), он остается самым неэффективным. Уже для 1000 элементов число сравнений выражается внушительной величиной порядка 500 тысяч.
Программная реализация включает двойной цикл: внешний реализует основные шаги алгоритма, внутренний сравнивает и переставляет элементы, начиная с конца массива.
for i:= 2 to n do.
begin.
for j:= n downto i do.
if a [j-1]> a [j]then.
begin temp:= a [j-1]; a [j-1]: = a [j]; a [j]: = temp; end;
end;