Математическое моделирование равномерности дождевания машиной непрерывного поступательного движения по результатам испытания аппарата радиальным методом

Целью исследования являлось совершенствование оценки равномерности дождевания машиной непрерывного поступательного движения по результатам испытания аппарата радиальным методом. Метод исследования — математическое моделирование функционирования четырех аппаратов кругового действия на машине непрерывного поступательного движения с использованием результатов испытания аппарата радиальным методом. Алгоритм расчета, рекомендованный ГОСТ ИСО 7749−2-2004, усовершенствован для минимизации ручных операций расчета и измерения. Алгоритм реализован в программе для ЭВМ. Программа CDU (B) реализует усовершенствованный алгоритм. Программа рассчитывает матрицу доз полива на метровых квадратах зоны дождевания между позициями двух аппаратов. Поступательное движение машины моделируется суммированием доз по столбцам матрицы при постоянном X. По вектору доз после прохода машины вычисляется коэффициент равномерности полива по Христиансену. Расчет выполняется при различном шаге установки аппаратов, и так определяется оптимальное расположение аппаратов. Усовершенствованный алгоритм расчета показателей равномерности дождевания по результатам испытания аппаратов радиальным методом реализован в программе CDU (A) [1], позволяет выбрать оптимальный шаг установки аппаратов. Алгоритм расчета показателей равномерности при шаге установки аппаратов на трубопроводе, большем радиуса орошения аппарата моделирует работу двух аппаратов. При шаге установки аппаратов, меньшем радиуса орошения аппарата, моделируется работа четырех смежных аппаратов. Оптимальный шаг установки аппаратов i-Wob равен 14.5 метрам, что в 1.75 раза больше радиуса орошения аппарата и в 1.5 раза больше шага установки стационарных аппаратов при таком же допуске на равномерность. Двухсопловый аппарат, который по оценке стандарта не удовлетворяет требованиям равномерности орошения при B больше и равном 16 м на машине поступательного движения обеспечивает качественное распределение при шаге установки менее 24 метров Ключевые слова: расчет показателей равномерности, равномерность дождевания, равномерность полива, коэффициент равномерности Христиансена, коэффициент эффективного полива, коэффициент недостаточного полива, коэффициент избыточного полива Проектирование, испытания и настройка машин связаны со значительными затратами времени, трудовых и материальных ресурсов [1]. Применение систем автоматизированного проектирования для этих целей позволяет ускорить разработку машин при существенном снижении затрат. Оптимизация процесса работы дождевальных машин методом моделирования по критериям равномерности дождевания позволяет повысить вероятность качественной работы при изменении условий эксплуатации.

ГОСТ ИСО 7749−2-2004 рекомендует радиальный метод испытания аппаратов кругового действия, а оценку качества работы — моделированием распределения по схеме полнополевого метода с четырьмя стационарными аппаратами. Однако, при этом рекомендуются ручные операции интерполирования и суммирования интенсивностей от работы четырех аппаратов. Ручная работа с матрицами больших размеров неизбежно связана с ошибками. Только математические модели, реализованные на ЭВМ, позволят устранить этот недостаток. Кроме того, необходима разработка моделей расчета равномерности дождевания машинами непрерывного поступательного движения с аппаратами, испытанными радиальным методом.

Равномерность распределения дождя по орошаемой площади ГОСТ ИСО 7749−2-2004 рекомендует оценивать коэффициентом равномерности полива Кристиансена, вычисляемым по формуле:

дождевание непрерывный поступательный полив.

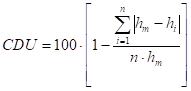
(1).

где — абсолютная величина отклонения измерения от среднего слоя осадков, мм;

— среднеарифметическое значение измерений; мм;

— измерение каждого дождемера, мм.

— количество измерений.

Испытание дождевальных аппаратов по ГОСТ ИСО 7749−2-2004 проводят полнополевым или радиальным методами. Полнополевой метод более трудоемкий, поэтому для аппаратов кругового действия рекомендуется радиальный метод, при котором дождемеры устанавливают на равных расстояниях вдоль радиуса, проведенного от места установки аппарата.

Измеряют количество воды в дождемерах при работе дождевального аппарата. Рассчитывают количество воды, собранной в имитируемых дождемерах, расположенных по схеме испытания машин полнополевым методом, то есть в центрах квадратных площадок. При этом вычисляется или графически замеряется расстояние каждого имитируемого дождемера от аппарата и интерполированием результатов радиального распределения вычисляется слой осадков в нем. Таким образом, получается матрица слоя осадков на всей зоне дождевания.

Имитируя расстояние между дождевальными аппаратами, выполняют накладку зон дождевания и рассчитывают суммарное количество воды, которое было бы собрано дождемерами, если бы они были расположены между четырьмя дождевальными аппаратами, идентичными испытуемому.

Вычисляют коэффициент равномерности по Христиансену.

Недостаток алгоритма состоит в применении ручных операций интерполирования и суммирования слоя осадков в зоне перекрытия и его пригодности только для стационарных систем и машин прерывистого поступательного движения.

Для оценки равномерности дождевания машинами непрерывного поступательного перемещения нами рекомендуется использовать следующий алгоритм математического моделирования:

• ? результаты испытания аппарата заносят в компьютер в виде двух векторов: IR — интенсивность дождевания в дождемерах, расположенных на различном расстоянии от аппарата; R — расстояние дождемера от аппарата;
• ? получают интерполяционную формулу зависимости интенсивности дождевания от радиуса;
• ? создают матрицу координат имитируемых дождемеров на зачетной площадке по схеме полнополевого опыта. Зачетной площадкой при расчете равномерности принимаем полосу между двумя смежными аппаратами, отстоящими друг от друга на расстоянии B (рисунок 1). Первый аппарат при этом расположен в начале координат, а второй — имеет координаты (+B, 0). Размер площадки по оси Y равен двум радиусам орошения. Имитируемые дождемеры расположены в центрах метровых квадратов, равномерно распределенных между позициями четырех аппаратов. Это условие выполняется, если шаг установки принять целым числом. На зачетную площадку попадает вода только от двух аппаратов при условии, если шаг установки больше радиуса орошения (рисунок 1, b). Если шаг установки меньше радиуса орошения (рисунок 1, d), то часть дождя от первого и от второго аппаратов не попадает на зачетную площадку (площади). Для полного учета воды, попадающей на зачетную площадку, необходимо моделировать работу третьего и четвертого аппаратов. Площадки и равны, поэтому на зачетную площадь попадает вода, количество которой равно расходу через аппарат, умноженному на время прохождения зачетной площади.
• ? вычисляют расстояния площадок матрицы от каждого из аппаратов;
• ? вычисляют интенсивности дождевания на каждой площадке от каждого аппарата;
• ? вычисляют суммы интенсивностей от четырех аппаратов;
• ? вычисляют матрицу доз полива в каждом дождемере умножением интенсивности на время прохождения машиной одного метра, то есть делением интенсивности на скорость поступательного движения машины. Оценку равномерности можно выполнять по равномерности доз или по равномерности интенсивностей. Результат будет одинаков;
• ? имитируют поступательное движение машины суммированием доз на линиях параллельных оси Y. Получают вектор доз .
• ? вычисляют среднеарифметическое значение дозы по вектору доз;
• ? вычисляют вектор модулей отклонений каждого значения дозы от среднего;
• ? вычисляют коэффициент Христиансена;
• ? задают цикл изменения шага установки аппаратов, т. е. расстояния между аппаратами на трубопроводе;
• ? расчет повторяют при различном шаге установки аппаратов;
• ? строят график зависимости коэффициента Христиансена от шага установки аппаратов;
• ? определяют оптимальный шаг установки аппаратов.

Основой для разработки программы расчета равномерности служат опубликованные ранее программы моделирования процессов дождевания [2, 3, 4, 5]. Программа [6] реализует усовершенствованный алгоритм расчета равномерности дождевания машиной непрерывного поступательного перемещения по результатам испытания аппарата радиальным методом.

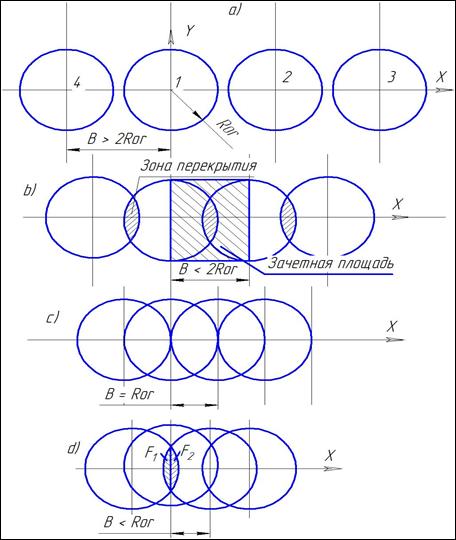
Рисунок 1 — Схемы зон орошения при различных расстояниях между аппаратами.

Покажем пример обработки результатов испытания аппарата i-Wob фирмы Senninger [7]. В проспекте фирмы приведен график зависимости интенсивности дождевания от радиуса. Выполним отсчет интенсивностей по графику через 0,5 метра. Создадим векторы IR и R (рисунок 2).

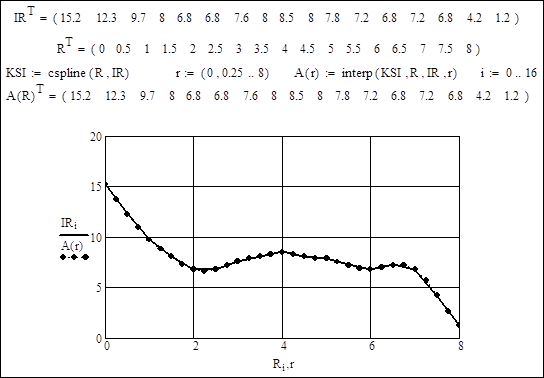
Рисунок 2 — Аппроксимация результатов испытания аппарата i-Wob.

Выполняем сплайн интерполяцию результатов испытания [8]. Для этого вычисляем коэффициенты KSI кубической интерполяции. Далее вычислим значения функция A®, строим графики исходных результатов IR и A®. Количество промежуточных точек вычисления функции A® в пять раз больше, чем у вектора IR. Аппроксимирующая функция точно проходит через эмпирические точки.

Для использования функции A® в программе расчета равномерности, её вычисление оформлено подпрограммой I©.

Далее по программе CDU1(A) [7] выполняем имитацию поступательного движения, получаем вектор доз вычисляем коэффициент Христиансена. Результаты расчетов представим графиком (рисунок 3).

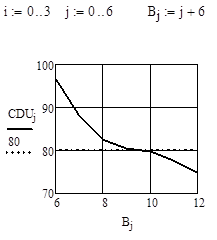
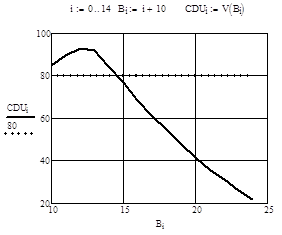
а б.

Рисунок 3 — Графики зависимости коэффициента равномерности от расстояния между аппаратами: а) — стационарными; б) — на трубопроводе машины непрерывного поступательного движения

Коэффициент равномерности полива Христиансена около 95 процентов получен при шаге установки 12,5 метров.

С непрерывного поступательного движения продольная неравномерность нивелируется и за счет этого можно допустить большее значение поперечной неравномерности.

Покажем второй пример расчета для аппарата, который по требования стандарта ГОСТ ИСО 7749−2-2004 не обеспечивает выполнения агротехнического допуска на стационаре. На рисунке 4 приведены графики зависимости коэффициента Христиансена по результатам испытания среднеструйного двухсоплового аппарата.

Результат расчета показателей равномерности приведен на рисунке 5.

Рисунок 4 — Результаты испытания двухсоплового аппарата и их аппроксимация.

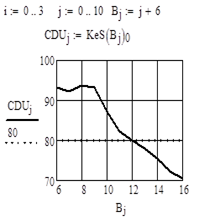
а б.

Рисунок 5 — Графики показателя равномерности дождевания, рассчитанные по результатам испытаний аппарата на рисунке 3 в зависимости от шага установки: а) — стационарных аппаратов; б) — на машине поступательного движения

Агротехнические нотмативы по равномерности выполняются при шаге установки менее двадцати четырех метров (рисунок 4, б). По результатам расчетов, рекомендуемых стандартом, такой аппарат непригоден для стационарных систем и машин, работающих позиционно, так как при показатель равномерности менее 70% (рисунок 4, а).

Предложенный метод моделирования использован для оптимизации расположения секторных насадок [9] и дальнеструйных дождевателей, работающих по кругу [10].

Выводы.

• 1. Усовершенствованный алгоритм расчета показателей равномерности дождевания по результатам испытания аппаратов радиальным методом реализован в программе CDU1
• 2. Алгоритм расчета показателей равномерности при шаге установки аппаратов на трубопроводе большем радиуса орошения аппарата моделирует работу двух аппаратов. При шаге установки аппаратов меньшем радиуса орошения аппарата моделируется работа четырех смежных аппаратов.
• 3. ГОСТ ИСО 7749−2-2004 необходимо дополнить предлагаемым алгоритмом расчета равномерности дождевания при фронтальном поступательном перемещении машины.
• 4. Оптимальный шаг установки аппаратов i-Wob равен 14.5 метрам, что в 1.75 раза больше радиуса орошения аппарата и в 1.5 раза больше шага установки стационарных аппаратов при таком же допуске на равномерность.
• 5. Двухсопловый аппарат, который по оценке стандарта не удовлетворяет требованиям равномерности орошения при, на машине поступательного движения обеспечивает качественное распределение при шаге установки менее 24 метров.

• 1. Кравченко, В. А. Повышение эффективности МТА на базе колёсных тракторов / В. А. Кравченко, В. А. Оберемок, Л. В. Кравченко. // Технология колёсных и гусеничных машин. — 2014.? № 6 (16). — С. 45…50.
• 2. Черноволов, В. А. Расчет показателей равномерности дождевания по результатам испытания аппарата радиальным методом / В. А. Черноволов, Л. В. Кравченко, Д. Н. Протасов.? Свидетельство о государственной регистрации программы для ЭВМ № 2 015 618 182 от 3.08.2015.
• 3. Черноволов, В. А. Расчет показателей эффективности дождевания на площади между четырьмя односопловыми аппаратами / В. А. Черноволов, Л. В. Кравченко.? Свидетельство о государственной регистрации программы для ЭВМ № 2 014 662 137 от 24.11.2014.
• 4. Черноволов, В. А. Расчет показателей эффективности дождевания одноструйными аппаратами при работе на двенадцати позициях / В. А. Черноволов, Л. В. Кравченко, О. В. Буткова.? Свидетельство о государственной регистрации программы для ЭВМ № 2 015 616 299 от 5.06.2015.
• 5. Черноволов, В. А. Оптимизация расстояния между насадками дождевальных машин фронтального действия / В. А. Черноволов, Л. В. Кравченко.? Свидетельство о государственной регистрации программы для ЭВМ № 2 014 617 785 от 04.08.2014
• 6. Черноволов, В. А. Расчет равномерности дождевания машиной непрерывного поступательного движения по результатам испытания аппарата радиальным методом / В. А. Черноволов, Л. В. Кравченко, Д. Н. Протасов.? Свидетельство о государственной регистрации программы для ЭВМ № 2 015 662 257 от 19.11.2015.
• 7. Сhernovolov, V. A. The uniformity of irrigation with single-jet sprinkler apparatus of rie action / V. A. Chernovolov, L. V. Kravchenko // Applied and Fundamental Studies. — 2014, November 29−30. — St. Louis, Missouri, USA. — P. 199−210.
• 8. Макаров, Е. Г. Инженерные расчёты в Mathcad 15. Учебный курс / Е. Г. Макаров. — СПб.: Питер, 2011. — 400 с.: илл.
• 9. Черноволов, В. А. Оптимизация размещения стационарных дождевателей методом математического моделирования / В. А. Черноволов, Л. В. Кравченко // Техническое и кадровое обеспечение инновационных технологий в сельском хозяйстве: материалы междунар. науч.-практ. конф., г. Минск, 23−24 октября 2014 г. / НИИ МЭСХ БГАТУ. — Минск, 2014. — С. 114−116.
• 10. Черноволов, В. А. Методика моделирования процесса дождевания дальнеструйными аппаратами при работе по кругу / В. А. Черноволов, Л. В. Кравченко // Вестник АПК Ставрополья: научно-практический журн. — 2014. — № 3(15). — С. 68−72.

References.

• 1. Kravchenko, V.A. Povyshenie jeffektivnosti mashinno-traktornyh agregatov na baze kolesnyh traktorov (increase of efficiency of mashinno-tractor units on the basis of wheel tractors) / V.A. Kravchenko, V.A. Oberemok, L.V. Kravchenko // «Tehnologija kolesnyh i gusenichnyh mashin». — 2014.? N_o 6 (16). pp. 45 — 49.
• 2. Chernovolov, V.A. Raschet pokazatelej ravnomernosti dozhdevanija po rezul’tatam ispytanija apparata radial’nym metodom / V.A. Chernovolov, L.V. Kravchenko, D.N. Protasov.? Svidetel’stvo o gosudarstvennoj registracii programmy dlja JeVM № 2 015 618 182 ot 3.08.2015.
• 3. Chernovolov, V.A. Raschet pokazatelej jeffektivnosti dozhdevanija na ploshhadi mezhdu chetyr’mja odnosoplovymi apparatami / V.A. Chernovolov, L.V. Kravchenko.? Svidetel’stvo o gosudarstvennoj registracii programmy dlja JeVM № 2 014 662 137 ot 24.11.2014. 4. Chernovolov, V.A. Raschet pokazatelej jeffektivnosti dozhdevanija odnostruj-nymi apparatami pri rabote na dvenadcati pozicijah / V.A. Chernovolov, L.V. Kravchenko, O.V. Butkova.? Svidetel’stvo o gosudarstvennoj registracii programmy dlja JeVM № 2 015 616 299 ot 5.06.2015.
• 5. Chernovolov, V.A. Optimizacija rasstojanija mezhdu nasadkami dozhdeval’nyh mashin frontal’nogo dejstvija / V.A. Chernovolov, L.V. Kravchenko.? Svidetel’stvo o gosudarstvennoj registracii programmy dlja JeVM № 2 014 617 785 ot 04.08.2014
• 6. Chernovolov, V.A. Raschet ravnomernosti dozhdevanija mashinoj nepreryvnogo postupatel’nogo dvizhenija po rezul’tatam ispytanija apparata radial’nym metodom / V.A. Chernovolov, L.V. Kravchenko, D.N. Protasov.? Svidetel’stvo o gosudarstvennoj registracii programmy dlja JeVM № 2 015 662 257 ot 19.11.2015.
• 7. Shernovolov, V. A. The uniformity of irrigation with single-jet sprinkler apparatus of rie action / V. A. Chernovolov, L. V. Kravchenko // Applied and Fundamental Studies. — 2014, November 29−30. — St. Louis, Missouri, USA. — P. 199−210.
• 8. Makarov, E.G. Inzhenernye raschjoty v Mathcad 15. Uchebnyj kurs / E.G.Makarov. — SPb.: Piter, 2011. — 400 s.: ill.
• 9. Chernovolov, V. A. Optimizacija razmeshhenija stacionarnyh dozhdevatelej me-todom matematicheskogo modelirovanija / V. A. Chernovolov, L. V. Kravchenko // Tehnicheskoe i kadrovoe obespechenie innovacionnyh tehnologij v sel’skom hozjajstve: materialy mezhdunar. nauch.-prakt. konf., g. Minsk, 23−24 oktjabrja 2014 g. / NII MJeSH BGATU. — Minsk, 2014. — S. 114−116.
• 10. Chernovolov, V. A. Metodika modelirovanija processa dozhdevanija dal'-nestrujnymi apparatami pri rabote po krugu / V. A. Chernovolov, L. V. Kravchenko // Vestnik APK Stavropol’ja: nauchno-prakticheskij zhurn. — 2014. — № 3(15). — S. 68−72.