Формообразование конструктивных сетей многогранных непологих куполов

Аннотация

В статье исследуется способ образования пространственных конфигураций в форме полуправильных многогранников. Приводится алгоритм геометрического расчета, позволяющий определить координаты узлов конструктивных сетей многогранных полусферических куполов, длины ребер и типоразмеры треугольных граней. Получены пространственные конфигурации в форме 20-, 80-, 320- и 1280-гранников. Результаты проиллюстрированы на 2-х примерах многогранников. Приведены геометрические схемы секториальных частей полусферических куполов по разрезке 320- и 1280-гранников с обозначением типовых узлов и треугольных панелей.

Ключевые слова: Икосаэдр, ребро, грань, полусфера, дублирование, секториальная часть, многогранник, купол, типоразмер, треугольная панель.

пространственный многогранник купол полусферический В трехмерном пространстве осуществимо построение пяти правильных многогранников, называемых платоновыми телами, к которым относятся:

ѕ Тетраэдр — 4 треугольника;

ѕ Куб (гексаэдр) — 6 квадратов;

ѕ Октаэдр — 8 треугольников;

ѕ Додекаэдр — 12 пятиугольников;

ѕ Икосаэдр — 20 треугольников.

Все вышеупомянутые многогранники могут быть вписаны в сферическую поверхность шара и имеют грани в форме равносторонних трех-, четырехили пятиугольников [1].

Наиболее широкое распространение для построения конструктивных сетей многогранных куполов получили пространственные точечные решетки икосаэдрального типа. Способы образования пространственных конфигураций в форме полуправильных многогранников рассмотрены в [2−6], где предпочтение отдается способу дублирования, который заключается в проецировании из центра на сферическую поверхность середин ребер исходного многогранника. При определении значений геометрических параметров и координат узлов конструктивных сетей многогранных полусферических куполов используется алгоритм расчета, основанный на применении способа центральной проекции. В качестве исходной конфигурации принимается икосаэдр, длина ребра l которого определяется выражением.

l=r? 1.05146r,(1).

где r — радиус сферы, описанной около многогранника.

Введем нумерацию вершин икосаэдра и поместим его в прямоугольной декартовой системе координат таким образом, чтобы центр описанной около многогранника сферы совпадал с началом координатных осей (рис. 1). Координаты 12 вершин правильного 20-гранника в долях радиуса r приведены в таблице 1.

Таблица 1.

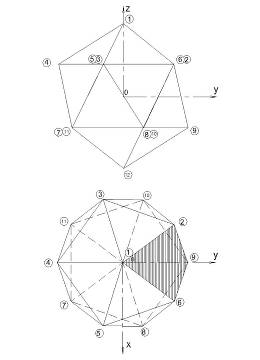
Рис. 1.

Пространственные точечные решетки икосаэдрального типа обладают пятикратной циклической симметрией[7,8], что позволяет при определении координат узловых точек применять процедуру дублирования только для секториальной части многогранника, выделенной на рис. 1 штриховкой. В рассмотрение принимаем сектор на плане многогранника, для которого координатная ось ОУ является осью симметрии. В этом случае значение координат узловых точек сектора, расположенных симметрично относительно этой оси, совпадают, за исключением значений координат по оси ОХ, которые одинаковы по абсолютной величине, но противоположны по знаку.

Пусть точка i (x_i, y_i, z_i) и j (x_j, y_j, z_j), являющиеся вершинами икосаэдра, соединены ребром l_ij(рис. 2). Из центра О через середину отрезка ij.

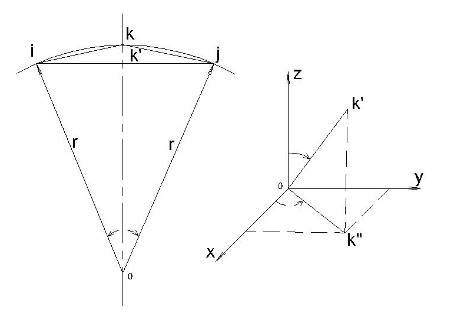
Рис. 2.

проводим луч ОК до пересечения со сферой радиуса r, описанной около многогранника. Требуется определить координаты точки К (x_k, y_k, z_k) и длины отрезков l_ik=l_kj.

Из формулы для отыскания длины отрезка, концы которого принадлежат сфере,.

l_ij=2rsin (2).

определяем центральный угол. Используя формулу (2), находим также длины отрезков ik и kj.

l_ik=l_kj=2rsin (3).

Координаты точки Kґможно получить с помощью следующих формул:

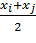
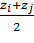
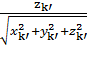
x_kґ=; y_kґ=; z_kґ=(4).

Затем находим угол ш_kмежду положительным направлением оси OZи лучом ОК:

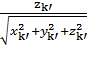
ш_k= arcos (5).

и угол ц_k между положительным направлением оси OX и проекцией луча ОК на плоскость ХОУ ц_k = arctg (6).

С помощью формул перехода от сферической системы координат к прямоугольной декартовой находим:

x_k= rcosц_ksinш_k

y_k= rsinц_ksinш_k(7).

z_k= rcosш_k

Таким образом, определяются координаты всех узловых точек секториальной части полученного 80-гранника. Координаты остальных узловых точек сети находятся с использованием формул поворота декартовой системы координат вокруг оси OZ.

Выполняя первую операцию дублирования над икосаэдром, получаем полуправильный 80-гранник, который характеризуется двумя типами треугольных граней (рис. 3). Полученный многогранник в диаметральных плоскостях трех направлений образует правильные десятиугольники, что позволяет, используя процедуру дублирования, получать пространственные конфигурации для построения конструктивных сетей куполов в виде полусферы с плоским опорным контуром многоугольного очертания.

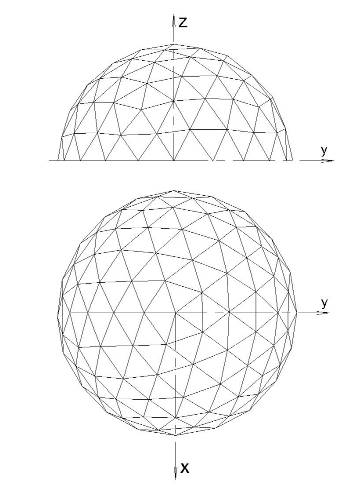
Рис. 3.

Выполнение второй и третьей процедур дублирования над икосаэдром позволяет с помощью изложенного алгоритма последовательно определить координаты узлов построенных конфигураций в форме 320- и 1280-гранников. Геометрические схемы этих многогранников представлены на рис. 4 и 5. Выполнение последующих процедур дублирования приводит к образованию многогранников со значительно большим числом граней (5120 и более), что усложняет использование таких конфигураций в качестве поверхностей купольных покрытий.

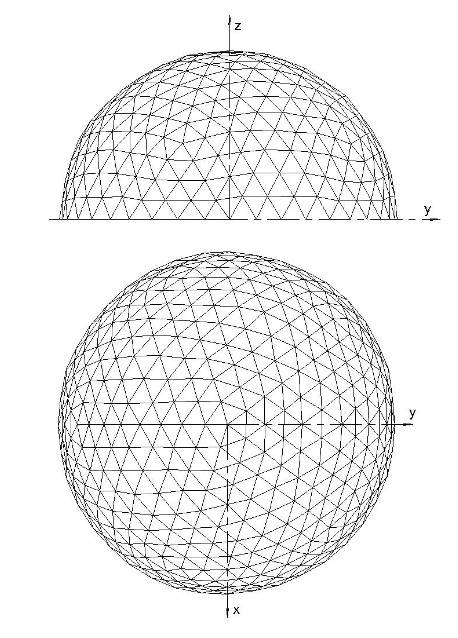
Рис. 4.

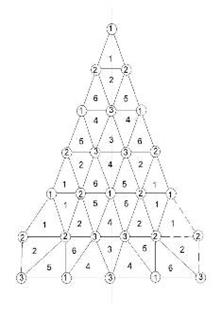
Рис. 5.

На рис. 6 и 7 представлены геометрические схемы секториальных частей полусферических куполов по разрезке 320- и 1280-гранников с обозначением типовых узлов и треугольных панелей. В таблицах 2 и 3 приведены значения длин ребер соответствующих типоразмеров.

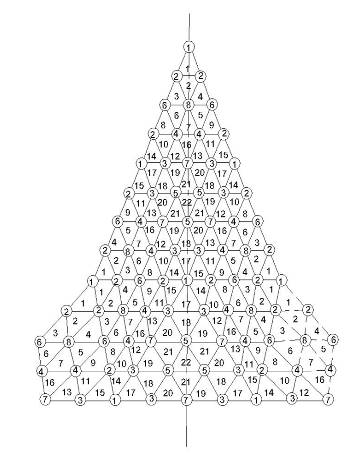
Рис. 6.

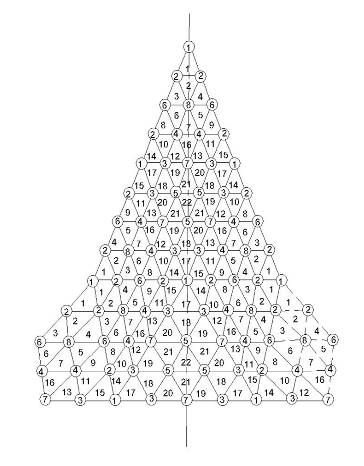
Рис. 7.

Таблица 2

Таблица 3.

Рассмотренная методика может быть использована при разработке архитектурных решений купольных сооружений (спортивных, выставочных и д.р.), состоящих их треугольных ячеек, в т. ч. при проектировании уникальных зданий и сооружений [9,10].

• 1. Ермолов В. В. Построение сетки геодезических куполов способом центральной проекции. — Строительная механика, расчет и конструирование сооружений: МАрхи, Москва, 1976, вып. 5, с. 79−83
• 2. Robert Jyhvyl; Translator: Ghanbar Ebrahimi — Housing and Building Research — Volume 2 — Edition 1, 1986, 354 p.
• 3. Василькин А. А., Рахмонов Э. К. Системотехника оптимального проектирования элементов строительных конструкций // Инженерный вестник Дона, 2013, № 4 URL: ivdon.ru/magazine/archive/n4y2013/2203.
• 4. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — Москва: Наука, 1984;832с.
• 5. Кабаков С. Ю., Грачев С. Е. Геометрическое формообразование многогранных сферических куполов // Архитектура и градостроительство на Дальнем Востоке. — Хабаровск, 1985. — с. 100−104.
• 6. Металлические конструкции. Справочник проектировщика. — Москва: Стройиздат, 1980;776с.
• 7. Журавлев А. А., Муро Г. Э. Новое конструктивное решение покрытия системы Цолингера // Инженерный вестник Дона, 2011, № 4 URL: ivdon.ru/ru/magazine/archive/n4y2011/706.
• 8. Gotz K.H., Hoor D., Mohler K., Holzbau Atlas. Munchen, 1978, 272 p.
• 9. Ammer Th., Brunaner A. Zollingers Rauten neu entdeckt. Bauen mit Holz, H.6, 1999. — pp.24−28
• 10. Фурсов В. В., Пурязданхах М., Бидаков А. Н. Сравнительный анализ результатов теоретических и экспериментальных исследований натурной арки из клееной древесины // Инженерный вестник Дона, 2013, № 2 URL: ivdon.ru/ru/magazine/archive/n2y2013/1608.

References

• 1. Ermolov V.V. Postroenie setki geodezicheskih kupolov sposobom central’noj proekcii. [A Handbook of Mathematics for Scientists and Engineers] - Stroitel’naja mehanika, raschet i konstruirovanie sooruzhenij: MArhi, Moskva, 1976, ed. 5, pp. 79−83
• 2. Robert Jyhvyl; Translator: Ghanbar Ebrahimi — Housing and Building Research. Volume 2 — Edition 1, 1986, 354 p.
• 3. Vasil’kin A.A., Rahmonov Je.K. Inћenernyj vestnik Dona (Rus), 2013, № 4 URL: ivdon.ru/magazine/archive/n4y2013/2203.
• 4. Korn G., Korn T. Moskva: Nauka, 1984;832p.
• 5. Kabakov S.Ju., Grachev S.E. Arhitektura i gradostroitel’stvo na Dal’nem Vostoke. Habarovsk, 1985. pp. 100−104.
• 6. Metallicheskie konstrukcii. Spravochnik proektirovshhika. [Metal constructions. Reference book of the designer.] Moskva: Strojizdat, 1980;776 p.
• 7. Zhuravlev A.A., Muro G.Je. Inћenernyj vestnik Dona (Rus), 2011, № 4. URL: ivdon.ru/ru/magazine/archive/n4y2011/706.
• 8. Gotz K.H., Hoor D., Mohler K., Holzbau Atlas. Munchen, 1978, 272 p.
• 9. Ammer Th., Brunaner A. Zollingers Rauten neu entdeckt. Bauen mit Holz, H.6, 1999. pp.24−28
• 10. Fursov V.V., Purjazdanhah M., Bidakov A.N. Inћenernyj vestnik Dona (Rus), 2013, № 2. URL: ivdon.ru/ru/magazine/archive/n2y2013/1608.