Отображение ортогональным проецированием четырехмерной гиперповерхности

Во многих прикладных задачах, связанных с профилированием режущего инструмента, определяют огибающую семейства поверхностей. Наряду с классическим подходом [1 — 2] к определению огибающей, в последнее время используется и новый [3], использующий отображение ортогональным проецированием поверхности на плоскость: [4 — 6] и другие. Так, если спроецировать график однопараметрического семейства двумерных поверхностей в пространство R⁴, то получим некоторую трехмерную гиперповерхность У. Дискриминанта этой гиперповерхности является огибающей рассматриваемого семейства. Исследование поверхности У при задании ее параметрическими уравнениями и уравнением в неявной форме проведено в работах [7 — 8], а его применение — в работах [9 — 10].

Отображение ортогональным проецированием четырехмерной поверхности и использование полученных результатов к определению огибающей двухпараметрического семейства поверхностей рассматривается ниже.

Пусть исходная четырехмерная гиперповерхностьзадана уравнением в неявном виде.

(1).

Рассмотрим отображения ортогональным проецированием этой поверхности по направлениям осей u и v на соответствующие координатные гиперплоскости.

Уравнения гиперплоскостей, касательных к гиперповерхности (1) в некоторой ее точке M(x₀, y₀, z₀, u₀, v₀), записываются в виде.

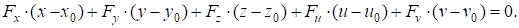
(2).

В точках гиперповерхности, в которых касательные гиперплоскости параллельны оси 0U, выполняется условие.

(3).

Будем рассматривать (3) как уравнение первой вспомогательной четырехмерной гиперповерхности Пересечение гиперповерхностей (1) и (3) определяют трехмерную гиперповерхность (рис.1), являющуюся криминантой гиперповерхности при ее ортогональном отображении вдоль оси u.

Четырех параметрическое множество плоскостей, касательных к гиперповерхности (3) в ее некоторой точке N (x₀, y₀, z₀, u₀, v₀), записывается в виде.

(4).

Гиперплоскости (2) и (4) пересекаются по трехмерным гиперплоскостям, касающимся гиперповерхности. В точках гиперповерхности (1), в которых касательные гиперплоскости параллельны оси 0V, выполняется условие.

(5).

Полученное уравнение рассматриваем как уравнение второй вспомогательной четырехмерной гиперповерхности Пересечение четырехмерных гиперповерхностей (1) и (5) определяет трехмерную гиперповерхность, являющуюся криминантой гиперповерхности при ее ортогональном отображении вдоль оси 0V. Тогда четырех параметрическое множество плоскостей, касающихся гиперповерхности (5) в ее некоторой точке K (x₀, y₀, z₀, u₀, v₀), записывается уравнением в виде.

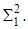
(6).

Пересечение трехмерных гиперповерхностей изадает двумерную поверхность, являющуюся криминантой гиперповерхности (1) при ее ортогональном отображении на гиперплоскость XYZ (по двум направлениям вдоль осей u и v).

Пусть точки M, N и K принадлежат не только соответствующим гиперповерхностям, но и двумерной поверхности. Тогда касательная плоскость к этой двумерной поверхности определяется в пересечении гиперплоскостей (2), (4), (6). Рассматривая уравнения (2) и (4) как систему линейных уравнений относительно (u-u₀) и (v-v_0), получим.

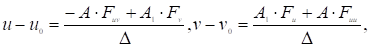
где.

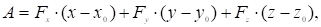
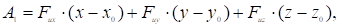
После подстановки полученных выражений в равенство (6), получим уравнение касательной плоскости к поверхности.

(7).

Тогда из приведенных уравнений следует, что криминанта гиперповерхности (1) при ее отображении ортогональным проецированием на гиперплоскости по направлениям осей 0U и 0V, определяется системой уравнений (1), (3) и (5), при условиях.

и.

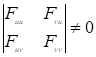
В качестве примера, иллюстрирующего достоверность полученных результатов, рассмотрим четырехмерную гиперповерхность, определяемую уравнением.

(8).

Эта гиперповерхность получена отображением двухпараметрического семейства сфер радиуса r c центрами на сфере радиуса R (рис.2) в гиперпространство XYZVU .

Тогда в соответствии с (3) уравнение первой вспомогательной гиперповерхности будет.

(9).

Откуда имеем.

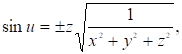
(10).

После подстановки зависимостей из (10) в равенство (9), получим уравнение трехмерной гиперповерхности, являющейся криминантой гиперповерхности (1) при ее отображении на гиперплоскость вдоль оси 0V:

(11).

Для исследования этой гиперповерхности рассечем ее гиперплоскостями. Так для Z=0, имеем Графиком этого уравнения является двумерная циклическая поверхность с плоскостью параллелизма 0XY (рис. 3). Сечением гиперповерхности (11) гиперплоскостью V=0 является двумерная поверхность, определяемая уравнением.

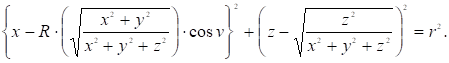
Ее график представлен на рис. 4.

Рассмотрим теперь отображение гиперповерхности (1) вдоль оси 0U. В этом случае уравнение второй вспомогательной гиперповерхности в соответствии с (5) получим в виде.

(12).

Откуда.

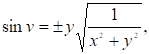
а (13).

Трехмерная гиперповерхность (12) является криминантой гиперповерхности (1) при ее отображении вдоль оси 0U. Криминанта гиперповерхности (1) при ее отображении вдоль осей 0U и 0V находится в пересечении первой и второй трехмерных гиперплоскостей. После подстановки выражений из (10) и (13) в (9) уравнение этой криминанты будет.

(14).

Графиком этого уравнения являются две сферы с центром в начале системы координат и радиусами (R+r) и (R-r) (рис. 5). После преобразований уравнение (14) можно представить в виде.

Это уравнение определяет алгебраическую поверхность четвертого порядка. Она распадается на две поверхности второго порядка — две сферы.

Таким образом, проведенные исследования гиперповерхности и ее отображения ортогональным проецированием на координатные гиперплоскости позволили получить в общем виде огибающую двухпараметрического семейства поверхностей, а также необходимые условия ее существования.

Полученные результаты апробированы на модели четырехмерной гиперповерхности, полученной отображением двухпараметрического семейства сфер в пятимерное пространство. Приведены как аналитические зависимости, так и соответствующие компьютерные полигональные модели сечений трехмерной гиперповерхности и двухмерной дискриминанты четырехмерной гиперповерхности.

четырехмерный гиперповерхность ортогональный проецирование.

• 1. Лашнев, С. И. Расчет и конструирование металлорежущих инструментов с применением ЭВМ [Текст]. / С. И. Лашнев, М. И Юликов. — М.: Машиностроение, 1975. — 392 с.
• 2. Litvin, F. L. Alfonso Fuentes Geometry and Applied Theory / Litvin, F. L. — Cembridge University Press, 2004. — 816 p.
• 3. Thom, R. Sur la theorie des envelopes / R. Thom // J. de math. pur et apple. — 1962. — Vol. 41. — № 2. — Р. 177−192.
• 4. Арнольд, В. И. Особенности гладких отображений [Текст]. — Успехи мат. наук. — 1968. — т. XXIII, вып. 1(139) — С. 4−44.
• 5. Брус, Дж. Кривые и особенности. / Дж., Брус, П. Джиблин [Текст]. — М.: Мир, 1988. — 262 c.
• 6. Платонова, О. А. Проекции гладких поверхностей [Текст]. / О. А. Платонова // Тр. Семинара им. И. Г. Петровского. — 1984. — т. 10. — С. 135−149.
• 7. Ляшков, А. А. Отображение ортогональным проецированием гиперповерхности на гиперплоскость [Текст]/ А. А. Ляшков, В. Я. Волков // Вестник Иркутского Государственного Технического Университета. — 2012. — № 2. — 18−22 с.
• 8. Ляшков, А. А. Отображение ортогональным проецированием поверхности, заданной параметрическими уравнениями [Текст] / А. А. Ляшков // Омский научный вестник. — 2012. — № 2(110). — 9−13 с.
• 9. Ляшков, А. А. Формообразование винтовой поверхности детали угловой фрезой [Электронный ресурс] / А. А. Ляшков // «Инженерный вестник Дона», 2012, № 3. — Режим доступа: http://www.ivdon.ru/magazine/archive/n3y2012/978 (доступ свободный) — Загл. с экрана. — Яз. рус.
• 10. Ляшков, А. А. Семейство поверхностей, заданное формулами преобразования координат, и его огибающая [Электронный ресурс] / А. А. Ляшков, А. М. Завьялов // «Инженерный вестник Дона», 2013, № 1. — Режим доступа: http://www.ivdon.ru/magazine/archive/n1y2013/1512 (доступ свободный) — Загл. с экрана. — Яз. рус.