Производственная отраслевая модель

Рассмотрим производственную статическую отраслевую модель в вариантной постановке на примере мясной промышленности, которая является типичной отраслью, находящейся под одновременным влиянием как сырьевого, так и потребительского факторов. Приближение производства мяса и мясных продуктов к районам сырья дает возможность сократить транспортные издержки на перевозку скота и обеспечить его эффективный откорм перед забоем. В то же время размещение предприятий мясной промышленности в центрах потребления целесообразно по той причине, что в данном случае потребитель получает более качественные мясопродукты. Кроме того, появляется возможность организации производственных сочетаний мясной и кожевенной промышленности.

Поскольку пример носит иллюстративный характер, ограничимся рассмотрением мясной промышленности в относительно небольшом районе. Пусть отрасль, представленная на этой территории двумя мясокомбинатами в пунктах A1 и A2, выпускает три вида продукции: мясо, колбасные изделия и мясные консервы. Предприятие, расположенное в пункте A1, выпускает в год 3 тыс. т мяса, 0,6 тыс. т колбасных изделий и 3,7 млн условных банок консервов. Предприятие, находящееся в пункте A2, выпускает в год 0,8 тыс. т мяса и 0,1 тыс. т колбасных изделий. Консервы оно не производит. Таким образом, суммарное производство мяса в районе составляет 3,8 тыс. т, колбасных изделий — 0,7 тыс. т, консервов — 3,7 млн банок. Предположим, что это удовлетворяет потребности населения в мясных продуктах с учетом их вывоза за пределы района. Однако известно, что через 10 лет потребности (с учетом вывоза за пределы района) в мясе составят b1 = 6,6 тыс. т, в колбасных изделиях — 62 =1,4 тыс. т, в мясных консервах — 63 = 5,5 млн банок. Следовательно, возникает задача развития мясной промышленности в рассматриваемом районе с тем, чтобы перспективные потребности в продукции отрасли были удовлетворены. При этом, естественно, нужно искать такой план развития и размещения отрасли, который мог бы быть осуществлен с минимальными капитальными и текущими затратами. Сельское хозяйство района предусмотрено развивать с таким расчетом, чтобы мясная промышленность была в достаточной мере обеспечена местным сырьем.

Для предприятия, расположенного в пункте 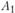, предусмотрено два конкурирующих варианта его реконструкции. Первый из них предполагает увеличение производства мяса до 4 тыс. т, колбасных изделий — до 1 тыс. т, консервов — до 5 млн банок. Подсчитано, что затраты на реконструкцию и производственные расходы составят в сумме 6,9 млн руб. Этот вариант реконструкции удобно записать в векторной форме: 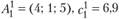. Нижний индекс в данном случае означает номер пункта производства, верхний — номер варианта. Второй вариант задается следующим вектором: 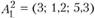и соответствующими затратами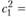 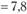млн руб.

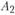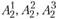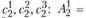
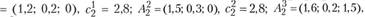
Для мясокомбината, расположенного в пункте , аналогично рассчитано три варианта реконструкции, задаваемые векторами с соответствующими затратами 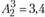. Таким образом, третий вариант реконструкции предприятия в пункте 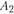предусматривает организацию производства консервов в объеме 1,5 млн банок.

Помимо пунктов 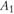и 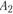, в районе имеются еще два пункта 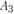и 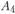, удобные для размещения в них предприятий мясной промышленности. Пункт 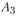находится в районе развитого мясного животноводства, так что в случае строительства в нем нового предприятия транспортные расходы по доставке сырья будут минимальными. Пункт 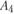более удален от сырьевой базы, но является крупным центром потребления мясных продуктов. Кроме того, в нем есть кожевенная промышленность, которую желательно перевести на мясное сырье. Пункты 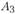и 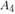имеют благоприятные транспортные условия. Таким образом, с экономико-географической точки зрения они представляются перспективными для строительства в них мясоперерабатывающих предприятий.

С учетом этого обстоятельства, для пункта 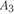рассчитаны три возможных варианта создания нового предприятия: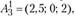

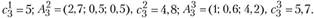
Для пункта 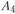аналогично рассчитаны два возможных варианта строительства нового предприятия: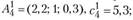

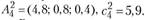
Рассчитанные варианты реконструкции существующих предприятий в пунктах 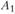и 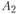, а также строительства в новых пунктах 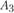и 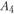, для наглядности сведены в таблицу (табл. 11.6).

Таблица 11.6

Варианты реконструкции существующих и строительства новых мясоперерабатывающих предприятий в районе

Потребности на перспективу в мясе, колбасных изделиях и мясных консервах в объемах 6,6 тыс. т, 1,4 тыс. т и 5,5 млн банок могут быть удовлетворены за счет различных сочетаний приведенных вариантов.

Так, эти потребности могут быть удовлетворены за счет сочетания вариантов 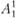и 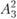, т. е. если для реализации будет принят первый вариант реконструкции предприятия в пункте 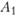и второй вариант создания нового предприятия в пункте 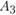. В этом случае объем производства мяса составит 4 + 2,7 = 6,7 тыс. т, колбасных изделий — 1 + 0,5 = 1,5 тыс. т, мясных консервов — 5 + 2,7 = 7,7 млн банок, а затраты — 6,9 +4,8 =11,7 млн руб. Потребности также могут быть удовлетворены и за счет сочетания вариантов ,.

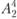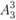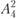, . В этом случае производство мяса в районе будет равно 1,6 + 1 + 4,8 = 7,4 тыс. т, производство колбасных изделий — 0,2 + 0,6 + 0,8 = 1,6 тыс. т, производство консервов — 1,5 + 4,2 + 0,4 = = 6,1 млн банок, а суммарные затраты составят 3,4 + 5,7 + 5,9 = = 15 млн руб. Ясно, что можно составить и другие комбинации рассчитанных вариантов, обеспечивающие удовлетворение указанных потребностей. Даже для приведенных 10 вариантов (см. табл. 11.6) число их сочетаний довольно значительно. Все сочетания вариантов, способные удовлетворить заданные потребности, различаются по затратам. Таким образом, определение оптимального перспективного плана развития и размещения мясной промышленности в данном районе заключается в отыскании такого сочетания рассчитанных вариантов реконструкции существующих и строительства новых предприятий, которое обеспечивало бы удовлетворение заданных потребностей с минимальными суммарными затратами.

Перейдем к формализации задачи. Введем в рассмотрение целочисленные переменные 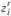. Для каждого из пунктов 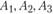и 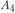вводится столько переменных 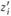, сколько для него рассчитано вариантов реконструкции или строительства. Так, для пункта 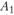вводятся переменные 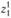и 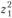, для пункта  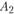— переменные 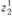, , 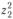, 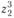для пункта 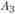- переменные 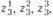для пункта 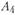- переменные 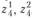. Смысл переменных 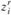, называемых интенсивностью использования r-го варианта (способа) в пункте 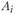состоит в следующем. Если 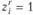, это означает, что r-й вариант в пункте 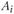подлежит реализации, если же 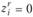, то этот вариант исключается из рассмотрения как неэффективный. Других значений переменные 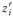принимать не могут.

В каждом из пунктов 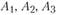и 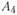может быть реализован лишь один вариант реконструкции существующего или строительства нового предприятия (варианты конкурируют между собой), т. е. в оптимальный план может войти только один из них. Математически это можно записать следующим образом:

(11.1).

Действительно, так как переменные 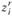могут принимать значения только 0 и 1, то условия (11.1) приведут к тому, что для каждого 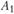не более одного 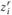окажется равным единице.

Далее необходимо, чтобы заданные потребности были удовлетворены. Математическая запись этих условий выглядит следующим образом:

(11.2).

Суммарные затраты на реализацию вариантов, входящих в план, составят следующие величину:

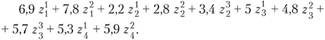(11.3).

Действительно, в результате решения задачи, в выражении (11.3) будут присутствовать затраты только по тем вариантам, где 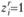, т. е. которые войдут в оптимальный план.

Таким образом, задача определения оптимального плана развития и размещения мясной промышленности в районе может быть сформулирована так: найти целые числа 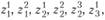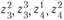, минимизирующие выражение (11.3) и удовлетворяющие ограничениям (условиям) (11.1) и (11.2). С математической точки зрения это задача целочисленного линейного программирования с булевыми переменными (т.е. принимающими лишь значения 0 и 1). Вполне очевидно, что чем больше рассчитано вариантов реконструкции существующих и строительства новых предприятий, тем больше число их сочетаний, из которых выбирается оптимальное, иными словами, тем шире допустимая область задачи. Одновременно ясно и то, что чем больше вариантов, тем больше и размерность задачи (так как для каждого из рассчитанных вариантов вводится переменная 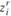) и, следовательно, увеличивается объем вычислений, необходимых для се решения.

Теперь нетрудно представить производственную отраслевую модель для общего случая. Известны пункты 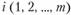размещения существующих и возможного строительства новых предприятий отрасли. Для каждого предприятия (как существующего, так и намечаемого) задается некоторый набор возможных вариантов (способов). Варианты могут отличаться друг от друга ассортиментом выпускаемой продукции, объемами производства каждого ее вида, текущими и капитальными затратами и т. д. Таким образом, каждому пункту 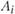ставится в соответствие система векторов 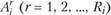. Вектор 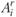представляет собой набор чисел 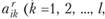где l — число видов продукции, которые может производить данная отрасль). Каждое число 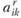означает объем производства вида продукции k в пункте 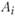по варианту r и задается в натуральных показателях. Если, например, некоторое 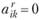, это означает, что по варианту r в пункте r продукт k не производится. В соответствии с вариантным способом постановки возможные варианты составляются заранее.

Вместе с каждым вариантом 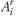задаются затраты на его реализацию 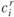. Экономическая природа затрат 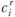может быть различной в разных задачах и зависит от ее постановки. Например, это могут быть капиталовложения, необходимые для осуществления данного варианта, себестоимость продукции, приведенные затраты и т. д.

Для каждого вида продукции задана нижняя граница (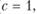 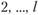) объема его производства. Величины 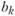задаются также в натуральных показателях, исходя из потребностей народного хозяйства и населения в продукции данной отрасли. Иными словами 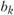- это потребность в виде продукции k, которая в обязательном порядке должна быть удовлетворена.

Задача заключается в том, чтобы при указанных заданных величинах найти оптимальный план развития и размещения предприятий отрасли, т. е. из всех возможных сочетаний заданных вариантов реконструкции существующих и строительства новых предприятий найти такую, которая при наименьших суммарных затратах обеспечивает потребное народного хозяйства и населения в продукции данной отрасли.

Эту задачу можно сформулировать в виде математической задачи: найти целые числа 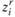(здесь и далее в задаче — 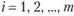; 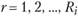), минимизирующие выражение.

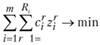(11.4).

и удовлетворяющие ограничениям (условиям):

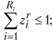(11.5).

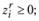(11.6).

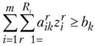(здесь и далее в задаче — 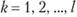). (11.7).

В зависимости от реальных условий развития рассматриваемой отрасли, кроме приведенных, в задаче может быть учтен и ряд других ограничений. Так, при наличии ограничения по капитальным вложениям в развитие данной отрасли следует ввести дополнительно и ограничение вида:

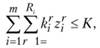
где 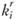- капитальные затраты по варианту г в пункте 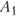; К — максимально возможный объем капитальных вложений.

При наличии ограничений по дефицитным видам сырья в задачу вводятся аналогичные ограничения. Если в пункте Ai по каким-либо причинам нельзя закрыть существующее предприятие или строительство нового предприятия обязательно (например, с целью увеличения занятости в этом пункте), ограничение вида 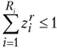заменяется ограничением 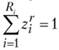, которое обеспечит выполнение указанных условий в оптимальном плане.

В задачах может быть учтена и взаимозаменяемость некоторых видов продукции. В таких случаях в исходной информации задаются объемы производства этих продуктов в каждом пункте по каждому варианту, а ограничения для этих продуктов — не по каждому из них, а для всех одновременно:

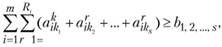
где 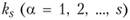- номера взаимозаменяемых продуктов; 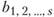- суммарная потребность в этих продуктах.

Если при постановке задачи встречаются взаимоисключающие (например, по условиям сырьевой базы) варианты различных предприятий, то в задачу водится ограничение вида.

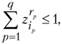
где 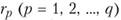- номера взаимоисключающих вариантов в пунктах .

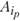Нами рассмотрена производственная отраслевая модель на минимум затрат. Как уже отмечалось, возможны и другие постановки задач, например на максимум выпуска дефицитного вида продукции. При такой постановке задаются ограничения по сырью 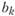, перерабатываемому предприятиями; 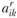означает объем переработки вида k сырья по варианту r в пункте 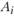. Обозначим через 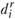объем производства данного продукта в пункте 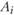по варианту r. Тогда задача формулируется следующим образом: найти целые числа 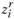максимизирующие выражение.

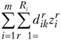
и удовлетворяющие ограничениям:

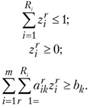
По своей структуре эта задача практически не отличается от задачи (11.4) — (11.7) и может быть решена теми же методами.

Производственно-транспортная отраслевая модель

Рассмотрим статическую модель отраслевых задач производственно-транспортного типа в вариантной постановке. Как и в случае производственной задачи, заданы пункты 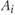(здесь и далее в задаче — 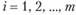) размещения действующих и возможного строительства новых предприятий отрасли, а также для каждого пункта набор вариантов с соответствующей каждому из них величиной затрат на его реализацию.

Пусть известны пункты 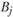(здесь и далее в задаче — 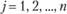) потребления продукции данной отрасли и для каждого из них заданы потребности в каждом виде производимой отраслью продукции. Обозначим через 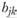объем потребности в виде k продукции в пункте 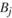. Требуется, чтобы все потребности были удовлетворены строго в заданных объемах. Обозначим через 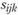(здесь и далее в задаче — 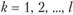) стоимость транспортировки единицы вида продукции k из пункта производства 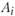в пункт потребления .

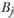Введем в рассмотрение новые переменные величины 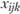, отражающие объем перевозок вида продукции k из пункта 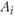в пункт 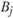. Тогда суммарные транспортные расходы по всей отрасли составят величину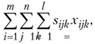

совокупные затраты на производство и транспортировку будут равны.

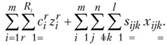(11.8).

Условие удовлетворения потребностей на территории пункта 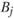в виде продукции k записывается следующим образом:

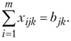(11.9).

Условие того, чтобы объем вывоза вида продукции k из пункта 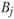не превышал объема его производства в этом пункте (в противном случае решение задачи потеряет смысл), в математической записи выглядит так:

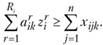(11.10)

Ясно, что объемы перевозок не могут быть отрицательными, поэтому:

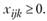(11.11).

И наконец, как и в производственной модели, нужно учесть, что в каждом пункте 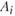может быть реализовано не более одного варианта:

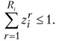(11.12)

Таким образом, задача состоит в том, чтобы найти числа 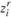(целые) и 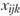(не обязательно целые), минимизирующие выражение (11.8) и удовлетворяющие ограничениям (11.9) — (11.12). Как и в случае производственной модели, могут быть учтены различные дополнительные условия, например ограничения по ресурсам, взаимозаменяемость различных видов сырья и продукции и др.