Уравнение множественной регрессии. 
Теорема Гаусса – Маркова

Почему же в практических приложениях оказались важными свойства оценок? Это связано с тем, что при моделировании реальных объектов, в том числе экономических, параметры являются не только числовыми коэффициентами при переменных, а несут на себе смысловую нагрузку, часто имеют размерность и по их величинам делают вывод о свойствах объекта.

Например, если модель (2.8) описывает зависимость расходов на потребление от располагаемого дохода, то параметр a1 есть предельные расходы по доходу и показывает, на сколько единиц изменяются расходы на потребление при увеличении дохода на одну единицу.

Теорема Гаусса — Маркова^[1] формулирует условия, при которых МНК позволяет получить наилучшие оценки параметров линейной модели множественной регрессии.

Несмотря на то, что Марков родился через год после смерти Гаусса, теорема была названа по их именам. Заслуга Гаусса — в разработке МНК, заслуга Маркова — в формулировке условий, при которых МНК позволяет получить состоятельные оценки.

Сформулируем постановку задачи. Мы имеем:

1) спецификацию модели в виде линейного уравнения множественной регрессии:

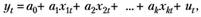(5.20).

2) выборку из n наблюдений за поведением переменных модели:

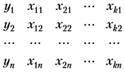(5.21).

Значения переменных в каждом наблюдении связаны между собой по правилу (5.20). Следовательно, в соответствие каждому наблюдению можно поставить уравнение:

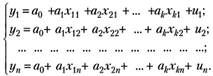(5.22).

Система уравнений (5.22) называется системой уравнений наблюдения или схемой Гаусса — Маркова.

Далее будем использовать следующие обозначения.

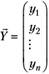- вектор наблюдений за эндогенной переменной; (5.23).

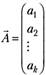- вектор параметров линейной модели; (5.24).

(5.25).

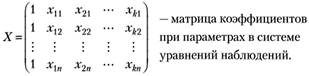
В матрице X в первом столбце записана единица.

Это «псевдопеременная» при параметре 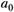. Эта единица появляется в матрице X только в тех случаях, когда спецификация модели содержит свободный параметр 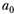. Если на этапе спецификации этот параметр не был записан, то и в матрице X столбец из единиц отсутствует.

В компактной записи с учетом введенных обозначений система уравнений наблюдений (схема Гаусса — Маркова) имеет вид:

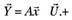(5.26).

Задача заключается в том, чтобы найти:

• 1) значения состоятельных оценок параметров модели (5.20);
• 2) значения несмещенных ошибок оценок параметров;
• 3) оценку ошибки случайного возмущения;
• 4) оценку наилучшего прогноза с помощью модели (5.20);
• 5) оценку ошибки прогноза.

Теорема начинается с описания условий, которые накладываются на вектор случайных возмущений. Эти условия принято называть предпосылками теоремы Гаусса — Маркова.

Теорему условно можно разбить на две части: " если" и " тогда" .

В первой части теоремы («если») формулируются условия на случайные возмущения, при выполнении которых МНК-оценки параметров линейной модели множественной регрессии отвечают свойствам несмещенности и эффективности. Эти условия принято называть предпосылками теоремы Гаусса — Маркова. Во второй части («тогда») формулируются оптимальные процедуры вычисления оценок параметров модели и основных функций этих параметров.

Теорема 5.1. «Если» :

1. Математическое ожидание случайных возмущений во всех наблюдениях равно нулю:

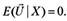(5.27).

2. Дисперсия случайных возмущений во всех наблюдениях одинакова и равна константе :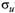

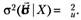(5.28).

3. Ковариация между парами случайных возмущений в наблюдениях равны нулю (случайные возмущения в наблюдениях независимы):

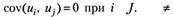(5.29).

4. Ковариация между вектором регрессоров и вектором случайных переменных равна нулю (регрессоры и случайные возмущения независимы):

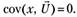(5.30).

" Тогда" : если матрица X (5.26) неколлинеарная (нет ни одного столбца, который можно было бы представить в виде линейной комбинации других его столбцов).

1. Наилучшая оценка вектора параметров линейной модели множественной регрессии вычисляется, как.

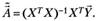(5.31).

Она соответствует методу наименьших квадратов.

2. Ковариационная матрица оценок параметров модели вычисляется, как.

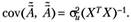(5.32).

3. Дисперсия случайного возмущения равна.

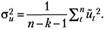(5.33).

4. Наилучший прогноз по модели (5.20) в точке.

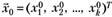вычисляется по правилу:

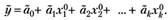(5.34).

5. Ошибка прогноза эндогенной переменной равна.

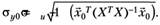(5.35).

Учитывая важность теоремы Гаусса — Маркова для эконометрики, рассмотрим ее доказательство.

Доказательство. Воспользуемся методом наименьших квадратов:

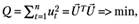(5.36) где.

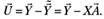(5.37).

Подставляя (5.37) в (5.36) и выполнив перемножения, получим:

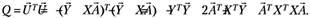(5.38).

Для получения необходимого условия экстремума дифференцируем (5.38) по вектору :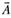

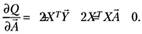(5.39).

Отсюда, система нормальных уравнений для вычисления оценок вектора 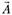имеет вид:

(5.40).

Тогда оценка вектора 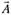есть.

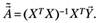
Выражение (5.31) доказано.

Замечание. Требование неколлинеарности матрицы X обеспечивает существование матрицы 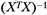. В противном случае процедура (5.31) неосуществима.

Покажем, что процедура (5.31) дает несмещенную оценку параметров модели множественной регрессии. Для этого необходимо вычислить математическое ожидание вектора оценки :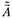

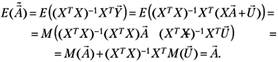(5.41).

Таким образом, несмещенность оценки (5.31) доказана. Отметим, что несмещенность достигнута в силу выполнения первой предпосылки теоремы Гаусса — Маркова.

Аналогичным образом доказывается справедливость выражения (5.32).

Остановимся более подробно на предпосылках теоремы Гаусса — Маркова.

Первая предпосылка (5.27) говорит о том, что во всех наблюдениях среднее значение (математическое ожидание) случайного возмущения равно нулю. Эта предпосылка отвечает за несмещенность параметров линейной модели множественной регрессии. Именно выполнение этой предпосылки обеспечило равенство нулю второго слагаемого в (5.41) и позволило получить несмещенные параметры модели.

Вторая предпосылка теоремы требует, чтобы во всех наблюдениях дисперсия случайного возмущения была одинаковой. Это свойство получило название свойства гомоскедастичности или однородности, или одинаковости дисперсий. В случае невыполнения данного условия говорят, что случайные возмущения в уравнениях наблюдения гетероскедастичные или неоднородные. Если случайные возмущения гетероскедастичные, то оценки параметров модели остаются несмещенными, но теряется эффективность оценки дисперсий параметров. Они, как правило, оказываются завышенными.

Третья предпосылка теоремы требует независимости случайных возмущений. Другими словами, каким бы не оказалось значение случайного возмущения в первом наблюдении, оно никак не сказывается на значениях случайного возмущения в любом другом наблюдении. Это свойство получило название неавтокоррелируемости случайных возмущений. Если это свойство не выполняется, то это так же сказывается на оценках дисперсий параметров модели. В этом случае дисперсии, как правило, занижены.

Четвертая предпосылка теоремы требует независимости случайных возмущений от значений регрессоров (экзогенных переменных). Как мы уже отмечали, рассматривая результат построения модели парной регрессии (5.9), невыполнение этого условия приводит к смещенности параметров модели. В тех случаях, когда значения регрессоров фиксированы, т. е. являются константами, эта предпосылка выполняется автоматически. Однако в ряде случаев регрессоры могут носить случайный характер. Например, если значения регрессоров в выборке есть результат измерений, или когда в качестве регрессора выступает лаговая эндогенная переменная.

• [1] Карл Фридрих Гаусс (30.04.1777−23.02.1855) — немецкий ученый — математик, физик, астроном. Андрей Андреевич Марков (14.06.1856−20.07.1922) — русский математик.