Понятие подмножества. 
Отношение включения

Множество А называют подмножеством множества S (или в множестве 5), если каждый элемент множества А является элементом множества S. Обозначение: Ис5.

Выражение AqS также читают: «А включено в 5», «А содержится в 5», «S содержит А», «А часть S». Знак с называют символом включения.

Запишем данное определение символически:

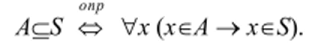
Из определения вытекает: множество А является подмножеством в S тогда и только тогда, когда из предложения (хеА) следует предложение (xeS).

Построим отрицание к тому, что AczS. По законам логики имеем:

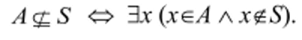
Итак, предложение «Множество А не включено в S» равносильно предложению «Существует элемент множества А, который не лежит в S».

Два множества А и В формально можно соединить знаками включения двумя способами: A (z.B и ВсА. Каждое из этих выражений определяет предложение, которое может быть истинным или ложным. Второе включение В<^А (также пишут А^В) по отношению к первому называют обратным. Не всегда из справедливости одного из включений следует истинность другого включения.

Пример 6.2.1. Имеет место включение {—2;2} с {—2;0; 1 ;2}, так как оба числа (-2) и 2 являются элементами множества {—2;0; 1 ;2}. Однако {—2;0; 1 ;2} не включено в {—2;2}, так как, например, 0 г {-2;2}. •.

Пример 6.2.2. Пусть А — множество всех ромбов, В — множество всех квадратов.

А? В, так как существует ромб, не являющийся квадратом.

В с: А, так как любой квадрат является ромбом (что вытекает из определений данных фигур).

Друг ими словами, множество всех квадратов является подмножеством множества всех ромбов. •.

Пример 6.2.3. {х | *:12}с{* | дг:3}, так как *:12=>*:3 (обоснуйте самостоятельно). Однако обратное включение неверно, гак как х:3фх':2 (приведите контрпример). •.

Из определения вытекает, что-то есть каждое множество является подмножеством самою себя.

Возьмем вместо А пустое множество. Тогда утверждение 0qS равносильно V* (хе0 xeS). Так как посылка импликации всегда ложна, то для любого объекта д; импликация принимает истинное значение. Значит, утверждение 0qS верно. Итак, пустое множество является подмножеством любого множества.

Вывод: у любого непустого множества всегда есть два подмножества — само множество и пустое. Их называют тривиальными подмножествами. Само множество также называют несобственным подмножеством.

Подмножество в S называется собственным, если оно не совпадает с S. Запись AaS^[1] означает, что А является собственным подмножеством в S:

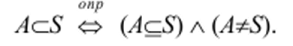
Знак <= называют символом строгого включении.

Мы имеем два отношения: отношение принадлежности элемента множеству (обозначаемое знаком е) и отношение включения множеств (обозначаемое знаком с). В общем случае это разные знаки. Например, {2}с{2,3}, но {2} *г{2,3}. Однако иногда между множествами можно поставить оба знака.

Пример 6.2.4. Множество А = {2} является элементом множества В = {1,2,{2}}. При этом А есть подмножество множества В, так вес элементы множества А лежат в В (в А есть только один элемент — число 2, который лежит в В).

Итак, {2}е{1,2,{2″ и {2}с{ 1,2,{2}}. •.

Пример 6.2.5. Рассмотрим плоскость а и прямую /, лежащую на этой плоскости. Если рассматривать прямую как элемент плоскости, то принято писать lea. Если же понимать прямую как множество точек, принадлежащих данной прямой, то это множество будет подмножеством множества всех точек плоскости. Тогда можно записать /са. •.

Пусть верны прямое и обратное включения AqB и B В этом случае для всех х выполняются импликации хеЛ —>хеВ и xgB->xеЛ, что равносильно тому, что для всех .v хеЛ тогда и только тогда, когда хеВ. Это означает, что множества, А и В совпадают:

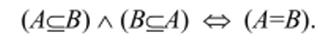
Эю простое соображение лежит в основе метода доказательства равенства множеств, называемого методом двойного включения: для того чтобы доказать, что множества, А и В равны, надо доказать прямое и обратное включения множ еств.

По сути, эта идея была продемонстрирована в примере 6.1.3, так как прямое включение A означает, что из предиката Р{х), задающего множество А, следует предикат Q{x), задающий множество В, а обратное включение означает, что из Q (x) следует Р (х). Рассмотрим еще один пример.

Пример 6.2.6. Возьмем множества:

А = {2п | neZ) — множество всех четных чисел,.

В — {хх=а+Ь, где а и b — нечетные числа} - множество всех чисел, каждое из которых является суммой некоторых нечетных чисел.

Докажем, что А=В.

Покажем справедливость включения А^В. Пусть хеА, тогда имеем х = 2w = (2/f-l)+1, то есть х представим в виде суммы двух нечетных чисел. Значит, хеВ.

Верно также обратное включение ВсА. В самом деле, пусть хеВ. Тогда х = (2/7+1)+(2А+1) = 2(/;+А'+1) = 2 т. Значит х — четное число, поэтому хеА.

Оба включения доказаны. Значит, множества А и В равны. •.

Упражнение. Докажите, что множества {2/7−1 пеZ} и {2/7+1 | неZ} равны, то есть оба определяют множество нечетных чисел.

Пример 6.2.7. Заметим, что множества А= {2я-1 | //eN} и В - {2/7+1 | /7 € N} нс равны, так как IgA, но 1 &В. Поэтому множество всех нечетных положительных чисел задаст только множество Л. При этом включение Л^В верно. •.

Пусть дано множество S. Семейство всех подмножеств множества S называется булеаном множества S (или степенью множества S) и обозначается В (5) или 2^s.

По определению В (5) = {X | AfcS}.

Ясно, что 0еВ (5) и SeB (S) для любого множества S.

Пример 6.2.8. Пусть S = {1,2,3}. Найдем булсан этого множества.

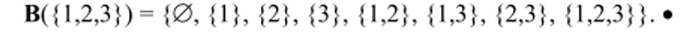
Заметим, что элементами булеана являются множества.

Термин «степень множества» и соответствующее обозначение мотивируются тем, что если мы имеем конечное //-элементное множество, то число элементов его булеана будет равно степени 2″. Рассмотренный выше пример иллюстрирует эту зависимость. Доказательство данного факта будет дано в главе 3. Там же будет рассмотрена формула, позволяющая находить у //-элементного множества число подмножеств, содержащих фиксированное число элементов.

• [1] В некоторой литературе знаком с обозначают произвольное подмножество.