Алгоритм решения линеаризованной системы разделения

На рис. 5.7 показано решение первичной подсистемы (шаг 0 и шаг 1) в блочном уменьшении по строкам для решения фундаментальной линейной системы. Шаг 1 делится на три части.

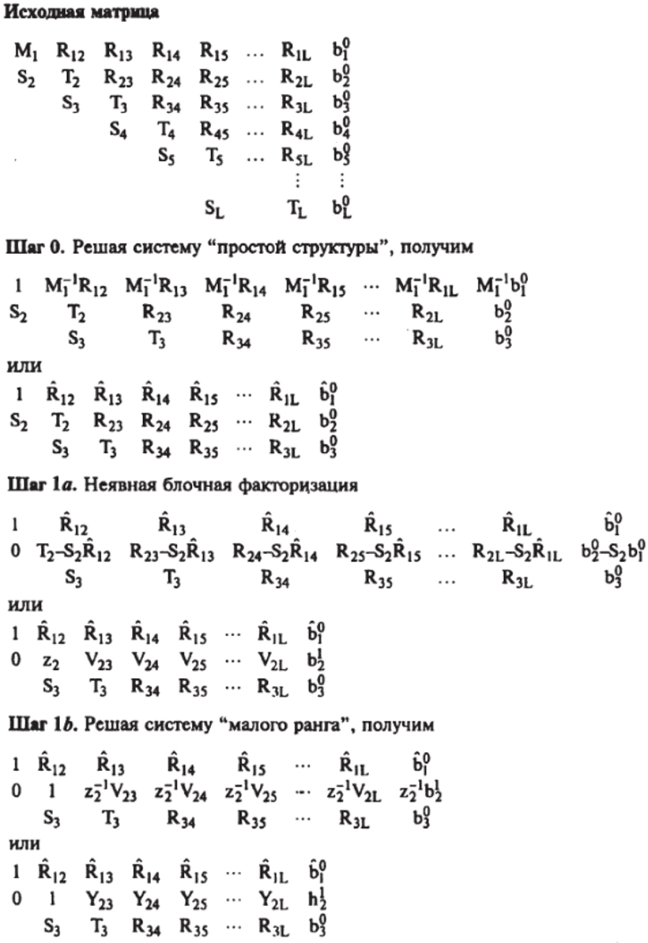
Puc. 5.7. Алгоритм блочно-построчного уменьшения (шаги 0, 1 а, Ь_У 1с).

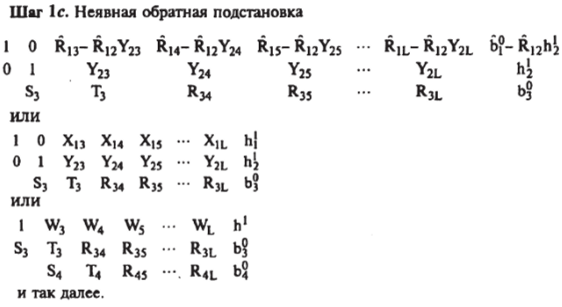
Рис. 5.7 (окончание).

Матрица вверху рис. 5.7 является обобщением Якобиана (рис. 5.6), расширенного правой частью системы (В-вектор). Алгоритм состоит в том, что после L — 1 шагов фундаментальная матрица «замещается» тождеством — единичной диагональной матрицей, а вектор правых частей — решением системы. Элементарное действие над строкой, производимое для расширенной матрицы, эквивалентно умножению обеих частей уравнения на такую же элементарную матрицу.

Например, шаг 0 (рис. 5.7), решающий первичные подсистемы, эквивалентен умножению первой блочной строки, чей ведущий элемент есть М, на Л/,^-1. Это равнозначно умножению обеих сторон первоначальной фундаментальной системы слева на элементарную матрицу первого типа Е¹:

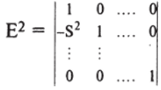
На шаге 1а строка 1 S2 раз вычитается из строки 2. Эта операция тождественна умножению обеих сторон результата шага О на элементарную матрицу второго типа Е²:

На шаге 1Ь решается «система малого ранга» — строка 2 умножается на (Г₂ — S₂ Л/,^-1 Ri₂)^_i, что эквивалентно умножению обеих частей результата шага 1 а на элементарную матрицу.

На шаге 1с используется операция над строкой того же типа, что и на шаге 1а, а именно Ri2(= A/f'Rn) — Это дает эффект «очистки» пространства, прежде занимаемого R12, где М — матрица простой структуры; R_v — правостороннее окаймление матрицы; 7} - матрица малого ранга; S/ - нижнее окаймление матрицы.

Теперь обозначим строки 1 и 2 как единую блочную строку, которая будет включена в операции над строкой 3 на шагах 2а, lb, 2с (не показано на рис. 5.7). После L — 1 таких шагов решение фундаментальной системы занимает пространство, первоначально занимаемое матрицей В. Число требуемых операций для данного алгоритма такое же, как для блочного гауссовского исключения (меньше, чем требуется для блочного гауссожордановского исключения), однако в данном алгоритме неявная блочная обратная подстановка дает возможность использовать меньшие объемы памяти.

Решение первичной подсистемы (шаг 0) находится решением независимых вторичных подсистем (БТДФ), каждая из которых решается методом блочного гауссовского исключения полностью до перехода к следующей подсистеме.

P-матрицы, появляющиеся в стандартном блочном гауссовском исключении (алгоритм Томаса), являются решениями третичных линейных подсистем. Они должны быть сохранены для обратной подстановки при решении вторичных линейных подсистем, однако, как только одна из вторичных подсистем решена, память может быть освобождена. Следовательно, если число В-матриц на диагонали наибольшей БТДФ есть р, число ячеек памяти, которое должно быть выделено для матрицы вторичной подсистемы, есть (р — 1) kL (где к = 2С + 1 — размерность матрицы В; L — число ненулевых столбцов в С-матрицах). Матрицы «правых частей» вторичных подсистем на рис. 5.6 имеют либо ненулевые «младшие» элементы, либо ненулевые, «старшие» элементы, либо не имеют ненулевых элементов. Для снижения количества расчетов каждая вторичная подсистема может быть уменьшена по строкам сверху вниз или снизу вверх, в зависимости от того, имеет ли «правосторонняя» матрица «младшие» или «старшие» ненулевые разряды. Если матрица «правых частей» не имеет ненулевых элементов, экономия в расчетах нереализуема.

Например, если вторичная подсистема, соответствующая стадиям 17−19 на рис. 5.6, решается стандартным гауссовским исключением сверху вниз, которое соответствует блочной LUфакторизации, количество операций умножения и деления равно рк^ — + 0(рк²), где р в данном случае равно 3; с другой стороны, если такие вторичные подсистемы решаются построчным уменьшением снизу вверх, которое соответствует блочной UL-факторизации, количество операций равно у рк^ъ — 2к? + 0(рк²). Разница появляется благодаря нулям в «младших» разрядах второго «правостороннего» матричного вектора. При расчете количества операций мы полагали, что матрица, А (позиции 17, 16) является полной (экономия из-за ее разреженности почти одинакова в любом случае).

При решении вторичных линейных подсистем ошибки, возникающие в решении третичных подсистем, включающих первую В-матрицу на диагонали, увеличиваются к концу первой подстановки (если используется стандартное исключение Гаусса сверху вниз), но не далее. Следовательно, чем меньше число третичных подсистем, тем более стабильны расчеты.

Таким образом, можно заключить, что в разработанном алгоритме перемещение дисперсных элементов в окаймление позволяет его оптимизировать во всех отношениях без дополнительных затрат. Разработанный алгоритм блочно-построчного исключения с шагом неявной блочной обратной подстановки для решения задачи линеаризации системы разделения минимизирует требуемые объемы памяти ЭВМ и позволяет снизить накапливаемые ошибки усечения.

Кроме того, сравнительный анализ эффективности предложенного алгоритма с существующими аналогичными ему алгоритмами показал, что смещение блочных дисперсных элементов к правому и нижнему окаймлениям позволяет оптимизировать алгоритм во всех отношениях.