Связь корректирующей способности кода с кодовым расстоянием

Степень различия любых двух кодовых комбинаций характеризуется расстоянием между ними по Хэммингу, или просто кодовым расстоянием.

Расстояние Хэмминга cl выражается числом позиций, в которых кодовые комбинации отличаются одна от другой. Чтобы подсчитать кодовое расстояние между двумя комбинациями двоичного кода, необходимо сложить по модулю две эти комбинации, а затем подсчитать число единиц в сумме. Поясним примерами.

Пример 1. Найти расстояние Хэмминга d между кодовыми комбинациями 10 101 011 и 11 111 011.

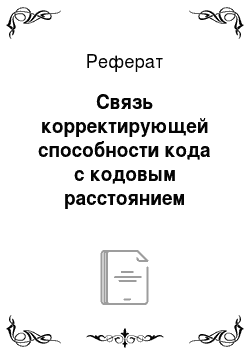
Произведем сложение по модулю два:

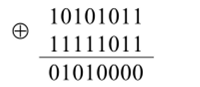
При сложении по модулю два переносов нет, сложение производится поразрядно по правилам: 000=0; 001 = 1; 101=0.

Сосчитав число единиц, в сумме получаем d = 2.

При мер 2. Найти расстояние Хэмминга между кодовыми комбинациями 10 101 111 и 111 100. Аналогично предыдущему примеру.

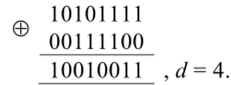
Для всех возможных комбинаций многоразрядного двоичного кода вводится понятие минимального кодового расстояния. Минимальное расстояние Хэмминга, взятое, но всем нарам возможных кодовых комбинаций данного кода, называется минимальным кодовым расстоянием. Поясним примером.

Для трехразрядного двоичного кода имеем комбинации: 000, 001, 010, 011, 100, 101, 110, 111. Подсчитаем расстояние Хэмминга для всех пар (табл. 12.1).

Таблица 12.1.

Минимальное кодовое расстояние c/_m;_n определяет способности кода обнаруживать и исправлять ошибки, возникающие при передаче данных.

Для рассмотренного трехразрядного двоичного кода d_min = 1. Если для передачи использовать все комбинации, то любая одиночная ошибка трансформирует переданную комбинацию в другую разрешенную кодовую комбинацию, поэтому возможности обнаружения ошибок не имеется.

Для создания возможности обнаружения ошибок при передаче поступим следующим образом. В трехразрядном коде для передачи исходной информации будем использовать два разряда, а третий передаваемый разряд для передачи будем формировать по правилу: его значение равно нулю, если число единиц в информационных разрядах четно, и равно единице, если число единиц в информационных разрядах нечетно. Поясним этот процесс таблицей.

В результате такого кодирования все множество двоичных трехразрядных кодовых комбинаций разбивается на две группы:

• • разрешенные — 000, 011, 101, 110;
• • запрещенные — 001, 010, 100, 111.

При передаче формируются и передаются помехоустойчивые кодовые комбинации, в которых число единиц четно. Если принята кодовая комбинация, содержащая нечетное число единиц (одна из запрещенных комбинаций), то можно утверждать, что при передаче произошла ошибка. Для разрешенных кодовых комбинаций нашего примера d_mm = 2, т. к.

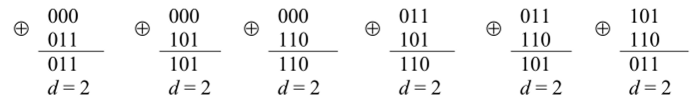
Таким образом, при d_mm = 2 обнаруживаются все однократные ошибки. Хэммингом доказано, что в общем случае для возможности обнаружения ошибок кратности г минимальное расстояние Хэмминга d_mm должно быть по крайней мере на единицу больше г, т. е. d_mj_n > г + 1.

В рассмотренной ситуации при появлении ошибки можно лишь сказать, что она произошла, но нельзя сказать, в каком разряде она произошла.

Для создания возможности исправления однократной ошибки поступим следующим образом.

В трехразрядном коде под информационный символ отведем один разряд, а два других отведем под избыточные контрольные символы (алгоритм формирования контрольных символов пока нс важен). Из всех трехразрядных кодовых комбинаций выберем разрешенными 000 и 111. Тогда при передаче и приеме информации могут возникать следующие ситуации (при возможности возникновения только одной ошибки):

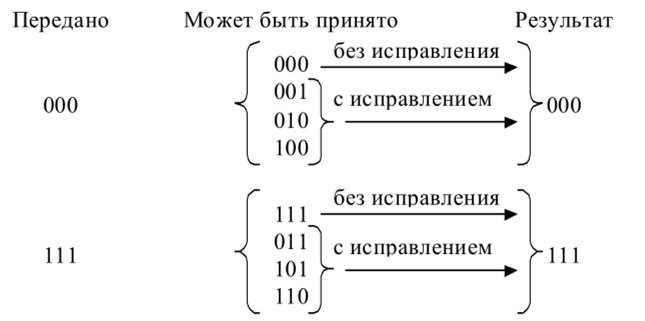
Видно, что все искаженные однократной ошибкой кодовые комбинации можно исправить. Расстояние Хэмминга между разрешенными кодовыми комбинациями для данного случая d_mn = 3.

Хэммингом доказано, что в общем случае для обеспечения кода возможностью исправления ошибок кратности 5 минимальное расстояние Хэмминга d_mi" должно находиться из условия d_min >25 + 1.

Для кода, позволяющего обнаруживать ошибки кратности г и исправлять ошибки кратности 5 (г > 5), минимальное расстояние Хэмминга выбирается из условия d_mm >r + S+ 1.

Если код должен обнаруживать двукратные ошибки и исправлять однократные, то t/_min должно быть равно 4. Поэтому код Хемминга с d_min = 3 может либо исправлять однократные ошибки, либо только обнаруживать однократные и двукратные ошибки.

Приведенные формулы нс позволяют определить требуемое количество контрольных (избыточных) символов и используются лишь для теоретической проверки разработанных кодов.