Необходимость задания класса решающих правил при изучении корреляции

Обычно при изучении связей в данных выделяют как минимум две группы признаков: прогнозирующие, или входные, признаки и целевые, или выходные, признаки. Обычно число целевых признаков невелико. Основные методы разработаны для случая, когда имеется только один целевой признак. Признак может выбираться в качестве целевого, если его трудно измерить или невозможно знать заранее. Поэтому хотелось бы получать такие «решающие» правила, чтобы для предсказания целевого признака было достаточно только измерения прогнозирующих признаков. Примеры областей и формулировок этой проблемы:

• а) химические соединения: входные признаки — особенности молекулярной структуры, целевые признаки — виды активности, такие как токсичность или лечебные свойства;
• б) виды зерна в сельском хозяйстве: входные признаки — свойства семян, грунта и особенности погоды, целевые признаки — урожайность или содержание клейковины;
• в) промышленные предприятия: входные признаки представляют технологии, инвестиции и кадровую политику, в то время как целевые признаки относятся к продажам и прибыли;
• г) муниципальные районы в маркетинговых исследованиях: входные признаки связаны с демографическими, социальными и экономическими характеристиками населения, целевые признаки — с покупательским поведением в данных районах;
• д) банковский кредит клиентам: входные признаки характеризуют демографические факторы и доход, а целевым является факт, окажется ли клиент потенциально безнадежным должником или нет;
• е) данные экспрессии (считывания) генов: входные признаки связаны с уровнем экспрессии материалов ДНК на разных стадиях болезни, а выходные признаки характеризуют уровень болезненных проявлений.

Решающее правило предсказывает значение целевого признака по значениям входных признаков. Правило называется классификатором, если целевой признак является категориальным, и регрессией, если целевой признак имеет количественный характер. Задачи с категориальными целевыми признаками подразумевают, что множество объектов разделено на классы, соответствующие отдельным категориям. Решение задачи корреляции в таком случае заключается в построении такого решающего правила, которое для каждого объекта определит, принадлежит ли он данному классу или нет.

Решающее правило строится на основе подмножества объектов, на котором значения целевых признаков известны. Это подмножество часто называют обучающим. Множество объектов, на котором значения целевых признаков считаются неизвестными, используется для тестирования качества решающего правила. Идея процесса обучения заключается в том, чтобы определить такое решающее правило, которое бы минимизировало разницу между предсказанными и наблюдаемыми значениями целевого признака на обучающей выборке данных в классе допустимых решающих правил. Структура такого процесса представлена на верхней части рис. 4.1.

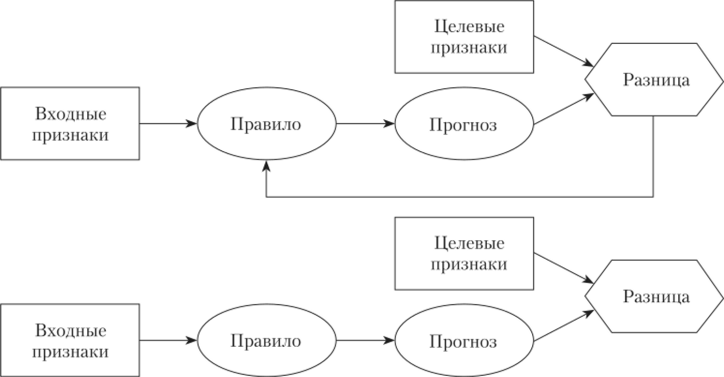
Рис. 4.1. Структура задачи обучения (тестирования):

наблюдаемые данные представлены прямоугольниками, вычислительные структуры представлены овалами, сравнение наблюдений с предсказаниями обозначено шестиугольником. В обучении (вверху) решающее правило подбирается так, чтобы минимизировать разницу между предсказанными и наблюденными значениями.

В тестировании (внизу) сформированное на этапе обучения правило используется для прогноза; здесь нет обратной связи с правилом Представление о том, что класс допустимых правил должен быть заранее задан, возникает поскольку обучающее множество конечно, так что, используя достаточное количество параметров, можно «подогнать» решающее правило таким образом, чтобы ошибок на обучающем множестве не было вообще. Но очевидно, что такое правило бы не сработало на тесте, так как подгонка захватывает все ошибки и шумы, неизбежные при сборе данных. Взгляните, например, на задачу двумерной регрессии. На рис. 4.2 изображены семь точек на плоскости (х, и), соответствующие наблюденным комбинациям входного признака х и целевого признака и.

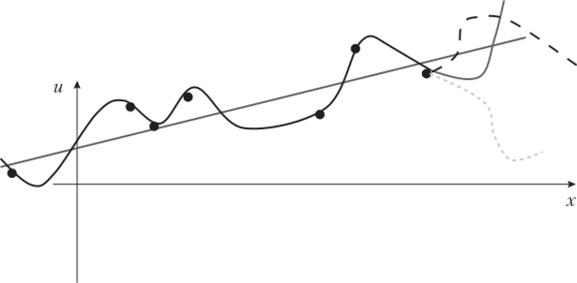
Рис. 4.2. Возможные графики взаимосвязи х и и но наблюденным данным (кружки) Семь точек — кружков на рис. 4.2 могут быть точно учтены полиномом шестой степени и = р (х) = я₀ + а_хх + а^² + %г³ + а_лх* + а$х⁵ + а^х⁶. В самом деле, при его оценке получим семь уравнений щ = р (х,) (i= 1,7), так что семь коэффициентов а_ь полинома могут быть точно определены (при обычных условиях «несингулярности»). Если число наблюденных точек — N_} то для точной оценки потребуется полином N-i степени.

Однако такой многочлен не сможет предсказать значения целевого признака ни внутри, ни за пределами диапазона. Кривая может пойти в любом направлении при самых небольших изменениях в данных.

Выбор правильного вида регрессионной функции, по-видимому, должен включать в себя понятие об «обобщающей силе» теории, определяемой этой функцией, которая для нашего случая сводится к отношению числа наблюдений к числу оцениваемых параметров: чем оно больше, тем лучше. Если это отношение относительно мало, статистики называют полученное правило избыточным или «переобученным». Избыточность обычно порождает малоинтересные (некачественные) прогнозы на вновь добавленных наблюдениях. Прямая линия не проходит ни через одну из семи точек, но выражает простую и падежную тенденцию. Следует отдать предпочтение этой прямой, поскольку она обобщает данные на более глубоком уровне: семь наблюдений обобщены здесь с использованием всего двух параметров: коэффициента наклона и свободного члена, в то время как многочлен не дает никакого обобщения, он включает в себя столько же параметров, сколько имеется объектов. Именно, но этой причине в задаче построения решающих правил в первую очередь нужно выбрать класс допустимых правил. Откуда его взять? К сожалению, на данный момент нельзя дать никакого общего совета, как это можно сделать, кроме совета «посмотреть на форму графиков разброса». Без знаний о предметной области нет почвы для выбора класса решающих правил.

Самый популярный подход — так называемая бритва Оккама. Согласно этому подходу решающее правило должно быть простым настолько, насколько это возможно. Считается, что данный совет реализует изречение средневекового британского философа Уильяма Оккама (ок. 1285—1349): «не следует множить сущности без крайней необходимости». Обычно это интерпретируется так, что при прочих равных, простейшее объяснение считается наилучшим. Математически это выражается как «принцип максимальной экономии», к которому обращаются, когда нет ничего лучшего. Будучи переформулирован как «принцип минимальности длины описания», этот подход может быть осмысленно применен к проблеме оценки параметров статистических распределений. Несколько более широкое и, возможно, более естественное толкование бритвы Оккама было предложено Банником [21]. В несколько измененном виде, чтобы избежать смешения терминов в данном случае, это толкование может быть представлено гак: найти допустимое решающее правило, которое объясняет наблюденные факты, используя наименьшее число свободных параметров [21, с. 448]. Однако даже в такой форме принцип не дает никаких рекомендаций о том, как выбрать адекватную функциональную форму. Например, какая из двух функций, степенная f (x) = ах^ь или логарифмическая g (x) = b • log (.r) + а, более предпочтительна для суммаризации графиков на рис. 4.3: ведь обе функции имеют два параметра — а и Ю

Следует отметить, что иногда уровень сложности определяется исходя из конкретной ситуации, а не общих соображений, что шутливо иллюстрирует рис. 4.4.

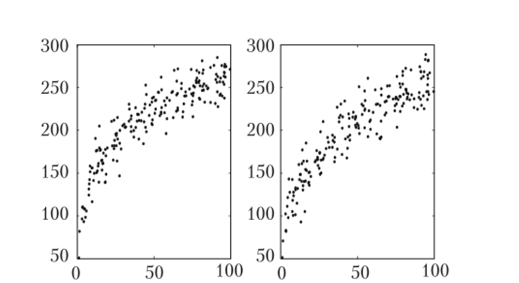
Рис. 43. Графики двух, не очень различимых, функций f (x) = 65х°'³ (справа) и g (x) = 501og (.v) + 30 (слева), обе с добавлением шума JV (0, 15).

Рис. 4.4. Пример сложного решающего правила.

Другие советы подобного рода относятся к так называемому принципу опровергаемое™ (фальсифицируемости) К. Поппера (1902—1994), который может быть выражен следующим образом: надо объяснить факты с помощью такого допустимого решающего правила, которое проще всего опровергнуть [21, с. 451]. По идее, для того чтобы опровергнуть теорию, нужно привести пример, ей противоречащий. Фальсифицируемость решающего правила может быть определена в терминах так называемой емкости или ВЧ-сложности (мера сложности, разработанная В. Н. Вапником и А. С. Червоненкисом в 70-е гг. прошлого века): чем ниже емкость, тем выше фальсифицируемость.

Рис. 4.5. Ситуации взаиморасположения точек на плоскости: три точки слева, четыре справа. Выделенное овалом подмножество нс может быть отделено с помощью прямой.

Поясним понятие ВЧ-сложности для случая категориального целевого признака, когда решающее правило — классификатор. Говорят, что набор классификаторов Ф разбивает обучающую выборку, если для любого разбиения обучающего множества на два класса в Ф найдется классификатор, точно воспроизводящий это разбиение. При заданном множестве допустимых классификаторов Ф, ВЧ-сложность задачи классификации есть максимальное число объектов, которое можно разбить классификаторами из Ф.

Например, точки в двумерном пространстве имеют ВЧ-сложность, равную 3, в классе линейных решающих правил. Действительно, любые три точки, не лежащие на одной прямой, могут быть разбиты прямыми линиями. Однако не все множества из четырех точек могут быть разбиты прямыми. Последние два утверждения проиллюстрированы соответственно на правой и левой частях рис. 4.5.

ВЧ-сложность — очень важная характеристика задачи коррелирования, особенно в рамках вероятностной парадигмы машинного обучения. В обычных условиях независимой случайной выборки данных надежный классификатор «с вероятностью а% будет точен в Ь% случаев, где b зависит не только от а, но также и от размера выборки и ВЧ-сложности» [21].

Задача изучения корреляции в таблице данных может быть сформулирована в общем виде следующим образом. Даны N пар (x_jyUj)_f i = 1, …, N_y где x_t — это векторы размерности р прогнозирующих (входных) значений х_{ — (x_i]y …, x_ip), a iij = (и_п,…, u_iq) — векторы размерности q целевых (выходных) значений (обычно q = 1). Зная эти пары, нужно построить решающее правило в предварительно заданном классе Ф допустимых правил F

такое, что в целом для наблюденных пар (х, и) разница между вычисленными й и наблюдаемыми и минимальна.