Алгоритм FOREL. 
Теория вероятностей и математическая статистика для экономистов

EOREL (от formal element, формальный элемент) — алгоритм кластеризации, основанный на идее объединения в кластер объектов в областях их наибольшего сгущения. Он предназначен для компьютерной реализации.

Цель кластеризации — разбить выборку на такое (заранее неизвестное) число кластеров, чтобы сумма расстояний от объектов кластеров до центров кластеров была минимальной по всем кластерам (т.е. задача алгоритма — выделить группы максимально близких друг к другу объектов, которые в силу гипотезы схожести и будут образовывать кластеры).

Минимизируемый алгоритмом функционал качества.

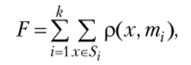
где первое суммирование ведется по всем кластерам выборки, а второе — но всем объектам х, принадлежащим текущему кластеру 5,; от, — — центр текущего кластера; р (х, от,) — расстояние между объектами.

Предположение, лежащее в основе алгоритма, — выполнение гипотезы компактности, предполагающей, что близкие друг к другу объекты с большой вероятностью принадлежат к одному кластеру.

Кластеризуемая выборка может быть задана описаниями объектов с помощью признаков, например координатами линейного пространства либо матрицей попарных расстояний между объектами. В реальных задачах необходимые данные собираются в процессе кластеризации. Среди исходных данных важен параметр R — радиус поиска локальных сгущений. Его можно как задавать из априорных соображений (знание о диаметре кластеров), так и настраивать скользящим контролем. В модификациях алгоритма возможно введение параметра k — количества кластеров.

Выходные данные алгоритма — кластеризация на заранее неизвестное число кластеров.

Принцип работы — рекуррентный. На каждом шаге случайным образом выбирается объект из выборки, описывается вокруг него сфера радиуса /?, внутри этой сферы выбирается центр тяжести, и он делается центром новой сферы (т.е. на каждом шаге сфера двигается в сторону локального сгущения объектов выборки, что соответствует стремлению захватить как можно больше объектов выборки сферой фиксированного радиуса). После того как центр сферы стабилизируется, все объекты внутри сферы с этим центром помечаются как кластеризованные и удаляются из выборки. Этот процесс повторяется до тех пор, пока вся выборка не будет кластеризована.

Структура алгоритма следующая.

• 1. Случайно выбирается текущий объект из выборки.
• 2. Помечаются объекты выборки, находящиеся на расстоянии менее чем R от текущего объекта.
• 3. Вычисляется их центр тяжести, этот центр помечается как новый текущий объект.
• 4. Повторяются шаги 2—3, пока новый текущий объект не совпадет с прежним.
• 5. Помечаются объекты внутри сферы радиуса R вокруг текущего объекта как кластеризованные, затем они удаляются из выборки.
• 6. Повторяются шаги 1—5, пока не будет кластеризована вся выборка.

Эвристические способы выбора центра тяжести:

• • в линейном пространстве — центр масс;
• • в метрическом пространстве — объект, сумма расстояний до которого минимальна среди всех внутри сферы;
• • объект, который внутри сферы радиуса R содержит максимальное количество других объектов из всей выборки;
• • объект, который внутри сферы малого радиуса г (г < R) содержит максимальное количество объектов из сферы радиуса R.

Алгоритм можно охарактеризовать следующими положениями.

Доказана сходимость алгоритма за конечное число шагов.

В линейном пространстве центром тяжести может выступать произвольная точка пространства, в метрическом — только объект выборки.

Чем меньше R, тем больше кластеров.

В линейном пространстве поиск центра происходит за время 0(п), в метрическом — 0(п²), где п — объем кластеризуемой выборки.

Наилучших результатов алгоритм достигает на выборках с хорошим выполнением условий компактности.

При повторении итераций возможно уменьшение параметра R для скорейшей сходимости.

Кластеризация сильно зависит от начального приближения (выбора объекта на первом шаге).

Рекомендуется повторная прогонка алгоритма для исключения ситуации «плохой» кластеризации по причине неудачного выбора начальных объектов.

Достоинства алгоритма:

• • точность минимизации функционала качества (при удачном подборе параметра R);
• • наглядность визуализации кластеризации;
• • наличие сходимости алгоритма;
• • возможность операций над центрами кластеров — они известны в процессе работы алгоритма;
• • возможность подсчета промежуточных функционалов качества, например, длины цепочки локальных сгущений;
• • возможность проверки гипотез схожести и компактности в процессе работы алгоритма.

Недостатки алгоритма:

• • относительно низкая производительность (решается введение функции пересчета поиска центра при добавлении каждого объекта внутрь сферы);
• • плохая применимость алгоритма при плохой разделимости выборки на кластеры;
• • неустойчивость алгоритма (зависимость от выбора начального объекта);
• • произвольное по количеству разбиение на кластеры;
• • необходимость априорных знаний о ширине (диаметре) кластеров.

После работы алгоритма над готовой кластеризацией можно производить некоторые действия. В частности, можно осуществлять выбор наиболее репрезентативных (представительных) объектов из каждого кластера. Можно выбирать центры кластеров или несколько объектов из каждого кластера, учитывая априорные знания о необходимой репрезентативности выборки. Таким образом, по готовой кластеризации имеется возможность строить наиболее репрезентативную выборку.