Основные элементарные функции
Степенная функция, у = хп. При п = 1 и при п = 2 функция, соответственно, принимает вид у = х и у = х2; в первом случае графиком является прямая, во втором — парабола (рис. 10.4). На этом же рисунке изображен график функции для п = 3 (кубическая парабола) и при п = В последнем случае функцию чаще записывают в виде: у = Vx. Логарифмическая функция, у = log,/г; а > 0, а ^ 1. Эта функция (рис. 10.6… Читать ещё >
Основные элементарные функции (реферат, курсовая, диплом, контрольная)
Перечислим основные элементарные функции, которые станут главным предметом нашего дальнейшего рассмотрения, они появляются при решении самых разнообразных задач и чаще других используются как в самой математике, так и в ее многочисленных приложениях.
Линейная функция. у = ах+ b, где аЬ — заданные действительные числа. Графиком линейной функции является прямая. Верно и обратное утверждение: всякая не вертикальная прямая является графиком некоторой линейной функции.
Пример ^.
Построить график функции у = -х + 1.
Чтобы провести прямую на плоскости хОу, достаточно построить две ее точки.
При х = 0 имеем у =1; полагая у = 0, находим х = -2. Через две точки М,(-2,0) и М2(0, 1) проводим прямую, которая является графиком данной линейной функции (рис. 10.2).
Функция определена на всей числовой прямой.
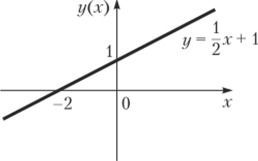
Рис. 10.2. Линейная функция.
Квадратичная функция (квадратный трехчлен): у = = ах1 + Ьх + с, где а, Ь, с — заданные действительные числа, а ^ 0. Графиком квадратичной функции является парабола, ось симметрии которой параллельна оси Оу. Высшая (или низшая) точка параболы (расположенная на оси симметрии) называется ее вершиной.
Свойства функции и вид ее графика (рис. 10.3) определяются в основном значениями коэффициента а и дискриминанта D = Ь2 — Аас.
Можно выделить полный квадрат из выражения для квадратичной.
b)2 Ь2— Аас
функции: у = ах~ + Ьх + с = а х+ — —, и (или) разложить на ли;
2а) Аа
нейные множители.
При D > 0 у = а (х — х{)(х — х2), при D = 0 у = а (х — х{)2, при D < 0 разложить на множители нельзя.
а> 0; оо), при а < 0 (-°°;—]. При b = 0 функция четная, при b ^ О.
4 а 4 а
функция ни четная, ни нечетная. При I) > 0 функция имеет два нуля: хх =
- -ь-ibл + Vd Л -ь п
- 2а 9 2 2а
лей нет.
Промежутки знакопостоянства:
у > 0 при х € (-°°; хх) U (х2; оо), у < 0 при х е (х,; х2);
если, а > О, D = 0, то у > 0 при х е (-°°; хх) U (х2; оо); если а > О, D > 0, то у > 0 при х е (-°°; +°°);
у > 0 при х € (х,; х2),.
2а
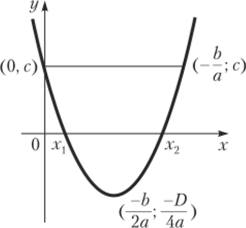
Рис. 10.3. Квадратичная функция.
Область определения: х е (-оо; +оо). Область значений функции при.
х2 =-о-> ПРИ 0 = 0 — один нуль — хх = —; при D < О ну;
если я > О, D > 0, го если «< О, D > 0, то j J < 0 п?и х е U (х2; оо);
если я < О, D = 0, то у < 0 при х € (-со; хх) U (х2; оо);
если а < О, D < 0, то у < 0 при х е (-°°; +°°).
Промежутки монотонности: п и > О IФУНКЦИЯ возрастает при х еЬ/2а +°°),.
ПРИ а | функция убывает при х е (-°°; -Ь/2а,
п и < О IФУНКЦИЯ возрастает при х е (-°°; -Ь/2а,
ПРИ а | функция убывает при х е -Ь/2а +оо).
Экстремумы квадратичной функции:
^ b D
при а > 0 xmin = - —, ymin = - —;
п Ъ Ъ
при а < 0 хтах = - —, утах =
2а 4 а
Далее, опуская детали, продолжим рассмотрение элементарных функций. В каждом случае читателю предлагается провести самостоятельное исследование свойств функции, обосновывающие приводимый график.
Степенная функция, у = хп. При п = 1 и при п = 2 функция, соответственно, принимает вид у = х и у = х2; в первом случае графиком является прямая, во втором — парабола (рис. 10.4). На этом же рисунке изображен график функции для п = 3 (кубическая парабола) и при п = В последнем случае функцию чаще записывают в виде: у = Vx.
Замечание. Обратим внимание на функцию у = л[х. Это соотношение равносильно тому, что х = у2 (у > 0). По если в этом уравнении поменять ролями ар;
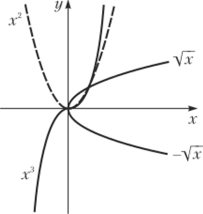
Рис. 10.4. Степенная функция.
гумент и функцию, т. е. поменять местами х и у, то мы придем к квадратной функции у = х2. Таким образом, в паре функций у = х2 и у = л[х одна получается из другой, если аргумент и функцию поменять местами. По определению, такие функции называются взаимно обратными.
Степенная функция не является периодической ни при каких п. Если п — натуральное число, то функция является четной при четном п и нечетной при нечетном п. Если п нечетное, то функция возрастает на (-°°; +°°); если п — четное, то убывает на (-°°; 0] и возрастает на 10; +°°); если п — целое отрицательное число, то в этом случае функция определена при всех значениях х, кроме х = 0.
Показательная функция, у = ах; а > 0, а ^ 1. Эта функция (рис. 10.5) определена при всех значениях ж. Ее область изменения (0; +°о). Если а > 1, то функция всюду возрастает; если 0 < а < 1, то убывает. Показательная функция не является периодической.
Логарифмическая функция, у = log,/г; а > 0, а ^ 1. Эта функция (рис. 10.6) определена при х > 0. Ее область изменения — вся числовая ось (—оо; +°о). Если а > 1, то она возрастает на (0; +°°); если 0 < а < 1, то убывает. Логарифм по основанию е называется натуральным логарифмом, для него принято специальное обозначение: log^x = In х.
Поскольку соотношение у = log"x, по определению логарифма, равносильно равенству х = ау, то функция у = а ' и у = lognx взаимно обратные. Поэтому для построения логарифмических кривых достаточно зеркально отразить графики соответствующих показательных функций, изображенных на рис. 10.5, относительно биссектрисы первого и третьего координатного углов.
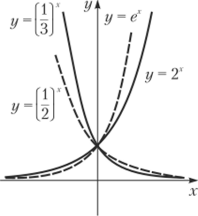
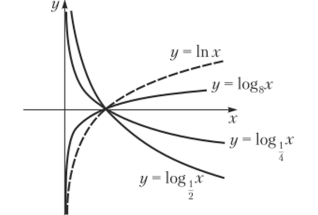
Рис. 10.5. Показательная функция Рис. 10.6. Логарифмическая функция Тригонометрические функции.
1. Синус: у = sin*. Эта функция определена на (-°°; +°°). Ее область из;
ТС
менения [-1; + 1|. Синус — нечетная функция. Возрастает на (— + 2тin;
тс тс Зтс ^
— + 2лп), убывает на (- + 2лгг, — + 2лп), где п е Z. Является периодичес кой функцией с периодом Т = 2л (рис. 10.7).
2. Косинус, у = cosх. Область определения (-°°; +°о). Область изменения [-1; + 11. Функция четная. Возрастает на (-л + 2ля; 2лп), убывает на (2лт? + л + 2пп), где п е Z. Является периодической функцией с периодом Т= 2л (см. рис. 10.7).

Рис. 10.7. Тригонометрические функции синус и косинус.
3. Тангенс: у = tgx. Область определения (— + пп; - + пп), где п е Z.
Область изменения (-°°; +°°). Функция нечетная. Возрастает всюду на К тс
- (— + ли; - + ли), и е Z. Является периодической функцией с периодом Г = л (рис. 10.8).
- 4. Котангенс: у = с tgx. Область определения (ли; л + ли), где и е Z. Область изменения (-оо; +оо). функция нечетная. Убывает на (ли; л + ли), и е Z Является периодической функцией с периодом Т = к (рис. 10.9).
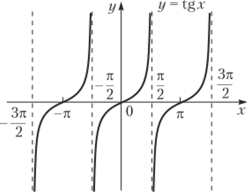
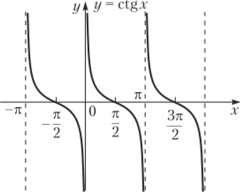
Рис. 10.8. Функция тангенс Рис. 10.9. Функция котангенс Обратные тригонометрические функции: у = arcsinx, у = arccosx, у = = arctgx, у = arcctgx. Как свидетельствует само название, эти функции являются обратными к соответствующим тригонометрическим функциям. Например, соотношение у= arccosx равносильно тому, что х = cos у (при этом у как радианная мера угла удовлетворяет ограничению: 0 < л < л). Поэтому для построения графиков обратных тригонометрических функций следует прибегнуть к уже испытанному приему: зеркально отразить соответственно синусоиду, косинусоиду, тангенсоиду и котангенсоиду относительно биссектрисы первого и третьего координатных углов, сохранив ту.
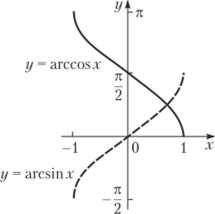
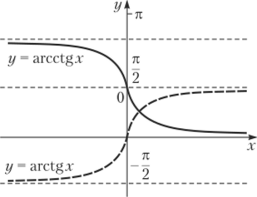
Рис. 10.10. Функции арксинус Рис. 10.11. Функции арктангенс и арккосинус и арккотангенс часть графиков, которая отвечает главным значениям угла. Графики обратных тригонометрических функций приведены на рис. 10.10 и 10.11.
Отметим, что аргумент х в формулах у = sin. г, у = cos а: и т. д. выражается в радианах. В элементарной тригонометрии при измерении углов за единицу отсчета чаще всего принимают центральный угол окружности, опирающийся на дугу, составляющую 1 /360 окружности. Этот угол равен одному градусу (градусная система счисления). Но в научных расчетах применяется и другая система счисления углов, когда за единицу отсчета принимают центральный угол, опирающийся на дугу, длина которой равна радиусу окружности. Этот угол называется радианом (радианная система измерения.
углов). Угол в 1 радиан равен углу в — ~ 57°, а угол в 180° равен углу в п ~ 3,141… радиана.
Сложная функция. Если у есть функция от и, переменная и есть функция от х, т. е. у = /(«), и = <�р (.г), то у называется функцией от функции, или сложной функцией: у =/|(р (.г)|.
Примеры сложных функций: у = logn(sinx), у = 2s'" / у = Vcosa7.
Элементарной функцией назовем функцию, которая получена из основных элементарных функций и констант при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
Алгебраические и трансцендентные функции. К алгебраическим функциям относятся:
а) многочлены — у = а0х" + aix" ' + arv" 2 +… + ап, в частности, линейная функция у = ах + b и квадратичная у = ах2 + Ьх + с;
б) дробно-рациональные функции 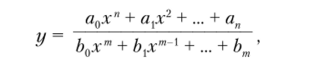
т.е. функции, определяемые как отношение двух многочленов;
в) иррациональные функции, т. е. функции у = f (x), где наряду с операциями сложения, вычитания, умножения и деления производятся также операции возведения в степень с дробными рациональными показателями, лг! + 'фх
например, у = л[х, у =, и т.н.
Ух2 + 1.
Вообще, алгебраической функцией называется функция у = /(х), которая удовлетворяет уравнению вида 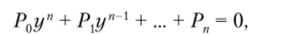
где Р0У Рр Р2уРп — многочлены, зависящие от х.
Функция, которая не является алгебраической, называется трансцендентной. Показательная, логарифмическая, тригонометрические функции я в л я ются транс цен дентн ы м и.