Системы линейных уравнений с двумя неизвестными

Рассмотрим систему линейных уравнений:

Аналогично, получим у = ^ ^ *. Заметим, что ^ ^ = а_{Ь₂ — Ь_ха₂ = А и назовем, А определителем системы.

с b ас

Аналогично, Д, = ^ _b' =c, b₂-bf₂ и Д_(/= _а' ^ = а, с₂ — с, а₂.

Получим, что х = у = — формулы Крамера для решения системы линейных уравнений.

Примеры

Находим определитель системы и вспомогательные определители:

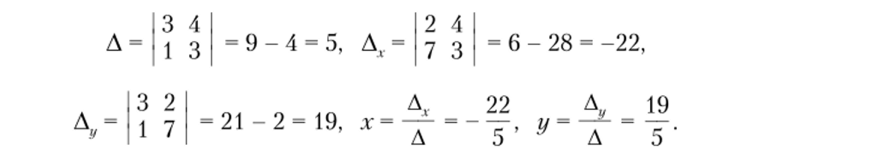
Выводы.

• 1) Если, А ^ 0, то система имеет единственное решение.
• 2) Если Д_д. = А_;/ = А = 0, то система имеет бесконечное число решений.
• 3) Если, А = 0, а А_Л. или, А ^ 0, то система не имеет решений.

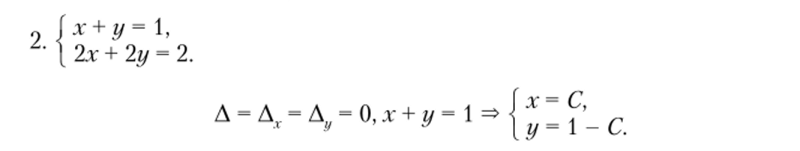
Указанные формулы Крамера работают для систем с п —числом неизвестных, но при этом существенно возрастают трудности вычисления определителей /7-го порядка.

10.6.3. Метод последовательного исключения неизвестных (метод Гаусса) Любая линейная система.

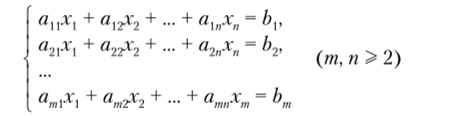
может быть записана в виде так называемой векторной форме Ах = Ь, где.

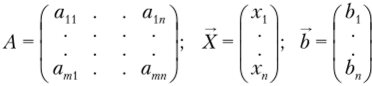
при этом система однозначно определяется так называемой «расширенной» матрицей:

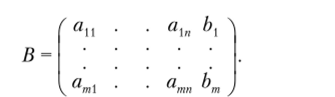
Последнее представление можно считать компактной записью самой системы, где j-я строка соответствует j-му уравнению системы.

Известны элементарные преобразования, которые приводят к эквивалентной системе.

• 1. Перемена местами любых двух строк матрицы или любых двух уравнений системы.
• 2. Умножение любой строки матрицы или любого уравнения системы на число, отличное от нуля.
• 3. Прибавление к какой-либо строке матрицы (или другого уравнения), умноженной на некоторое число.

Сущность метода Гаусса состоит в том, что с помощью элементарных преобразований любая система (и соответствующая расширенная матрица системы) может быть приведена к ступенчатому верхнетреугольному виду (при котором в расширенной матрице все элементы, лежащие ниже главной диагонали, равны нулю), допускающему непосредственное решение.

Пример Для линейной системы.

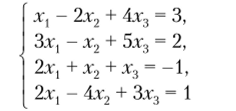
запишем «расширенную» матрицу.

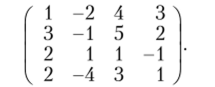
Оставляя первую строку без изменения и вычитая утроенную первую строку из второй и удвоенную первую строку из третьей и четвертой, получим эквивалентную систему:

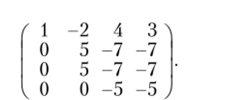
Вычитая вторую строку из третьей, придем к более простой матрице:

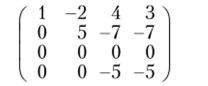
и после вычеркивания третьей строки получим в итоге верхне-треугольную ступенчатую матрицу: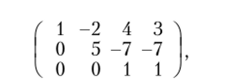

которая соответствует системе 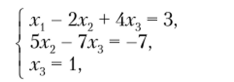имеющей решение х₃= 1, х₂ = 0, х, = -1.

10.6.4. Решение системы линейных уравнений с помощью обратной матрицы Рассмотрим систему, у которой число уравнений равно числу неизвестных, т = п.

АХ = В, где А = (a_tj) — квадратная матрица порядка п. При решении такой системы возможны два случая.

1. Матрица А = (аА — не вырождена (т.е. ее определитель Д ^ 0). В этом случае существует обратная матрица А¹. Уравнение АХ = В умножим слева на А ', получим.

А’АХ = А’В,

так как А 'А = Е (единичная матрица), то решение системы будет Х = Л 'В.

Итак, система имеет единственное решение, которое находится с помощью обратной матрицы по формуле.

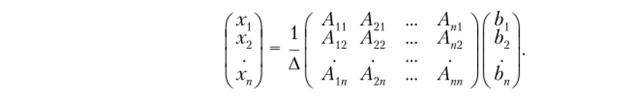
Пример Решить систему с помощью обратной матрицы:

Решение.

1. Установим, булет ли основная матрица системы невырожденной, для этого найдем ее определитель:

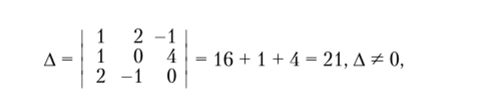
следовательно, А — невырожденая.

Решение X ищем по формуле X = А 'В. Найдем обратную матрицу:

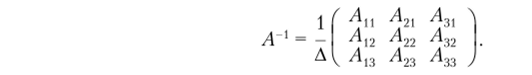
Вычислим все алгебраические дополнения:

2. В случае, если матрица будет вырожденной, т. е. детерминант ее будет ра вен нулю (Д = 0), то найти решение с помощью обратной матрицы будет невоз можно.