Непрерывные и дискретные случайные величины

Определение 2.13. Функцией распределения случайной величины X называется функция F_x(x) = Р (Х < х).

Свойства функции распределения следующие:

1) lim F (x) = 0;

t~*~ оо.

2) lim F (x) = 1;

{ —" Too.

• 3) F (x) является неубывающей;
• 4) F (x) является непрерывной справа.

Здесь и далее мы будем обозначать случайные величины заглавными буквами (X), а их соответствующие реализации — строчными (.г).

Определение 2.14. Если случайная величина принимает конечное или счетное множество значений, то она называется дискретной.

Дискретные случайные величины удобно задавать с помощью таблицы, в первой строке которой перечислены значения, которые принимает случайная величина, а во второй — соответствующие вероятности:

Определение 2.15. Если существует кусочно-непрерывная функция /(.г), такая что F%(x) = /(х), то случайная величина X называется непрерывной, а /(.г) — ее функцией плотности.

Свойства функции плотности следующие:

• 2) f (pc)dx= 1.
• -OO

Для непрерывных случайных величин вероятность попадания в точку (конкретное значение) равна нулю — для этих случайных величин обычно имеет смысл вычислять вероятность попадания в интервал.

Утверждение 2.1. Для случайной величины X с функцией плотности f (x) вероятность попадания в интервал [а; b] вычисляется по формуле.

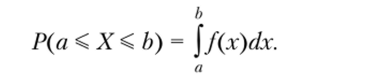
Основными числовыми характеристиками случайных величин являются математическое ожидание Е (Х) — среднее значение случайной величины X — и дисперсия var (X) — мера отклонения от среднего^[1].

Определение 2.16. Математическое ожидание для дискретной случайной величины находится по формуле.

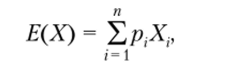
а для непрерывной случайной величины.

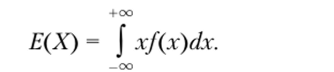
Определение 2.17. Модой случайной величины называется точка максимума функции плотности (для непрерывной случайной величины) или любое ее значение, которому соответствует максимальное значение вероятности (для дискретной величины).

Замечание 2.1. Мода случайной величины может быть неединственной.

Определение 2.18. Квантилем случайной величины порядка т называется точка Х_(т), являющаяся наименьшим решением уравнения F_x(x) = т, где F_x(x) — функция распределения случайной величины X.

Определение 2.19. Медианой случайной величины называется точка, являющаяся ее квантилем порядка 0,5.

Замечание 2.2. Таким образом, Р (Х < Х_{(0 5)}) = Р (Х > Х₍₀₅₎).

Определение 2.20. Дисперсией случайной величины X называется величина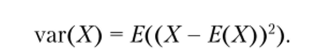

Определение 2.21. Ковариацией случайных величин X и Y называется величина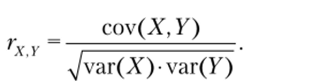

Определение 2.22. Коэффициентом корреляции случайных величин X и Y называется величина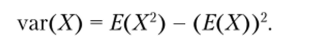

Рассмотрим свойства математического ожидания, дисперсии, ковариации и корреляции случайных величин.

• 1 .?(с)-с.
• 2. Е (сХ) = сЕ (Х).
• 3. Е (Х_х + Х₂) = Е (Х,) + ?(Х₂).
• 4. var© = 0.
• 5. var (cX) = c²var (X).
• 6. var (X, + X₂) = var^) + 2cov (X" X₂) + var (X₂).
• 7. cov (X_v X₂) = cov (X₂, X_{).
• 8. cov (oX_p AX_;) = abcov (X_v X₂).
• 9. cov (Xj, X₂ + c) = cov (X, X₂).
• 10. cov (X" X₂ + X₃) = cov (X_p X₂) + cov (Xp X₃).
• 11. cov (Xp c) = 0.
• 12. | r_x, Y< 1.
• 13. r_x, Y = ± 1 только в том случае, когда между X и Y существует точная линейная зависимость.

Здесь а, Ь, с — константы, а X, X, Х₂, Х₃ — случайные величины. Используя свойства для математического ожидания и дисперсии, можно доказать формулу для вычисления дисперсии:

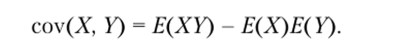
Также верна следующая формула для ковариации:

Утверждение 2.2. Если g (x) — достаточно гладкая функция (такая что приведенный ниже ряд сходится, а несобственный интеграл существует), то.

п

E (g (X)) = Tg (Xi)p_if если X — дискретная случайная величина, и E (g (X)) =

i= 1.

+оо.

= J g (x)f (x)dx, если X — непрерывная случайная величина с функцией.

— СО плотности /(дО;

Определение 2.23. Начальным моментом k-vo порядка случайной величины X называется величина т_к = Е (Х^к).

Определение 2.24. Центральным моментом k-vo порядка случайной величины X называется величина x_k = Е ((Х — E (X))^k).

Моменты случайных величин в основном используются для описания свойств этих величин.

Поскольку в практических задачах обычно исследуются несколько случайных величин, то необходимо рассматривать их совместные и условные распределения, так как это позволяет извлечь больше информации из данных.

• [1] В российской математической литературе приняты другие обозначения для данных величин (М — математическое ожидание, D — дисперсия), но так как в данной книге идет ориентация на пакеты программ, то обозначения этих и других величин в ней даны в соответствии с международной нотацией, используемой в этих пакетах.