Узлы модульного суммирования

Модульное суммирование, которое можно рассматривать как составную часть теории функций /с-значной логики, широко используется при построении криптографических генераторов псевдослучайных последовательностей с целью «улучшения» статистических характеристик выходных последовательностей, а также для обеспечения сложной зависимости знаков результирующей последовательности от промежуточных последовательностей, снимаемых с узлов и блоков генератора.

Будем рассматривать случайные величины г/, принимающие значения на множестве Z_m с вероятностями.

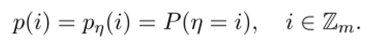
При этом множество Z_m рассматриваем как абелеву группу G = (Z_m, +) с операцией сложения по модулю га. При га = 2 соответствующие случайные величины называются двоичными.

Характеристикой статистического качества случайных величин 71 являются значения отклонений вероятностей Р (г) = г) от Другими словами, качество случайной величины определяется ее близостью к равномерно распределенной случайной величине.

Утверждение 5.18. Пусть заданы независимые двоичные случайные величины? j, j — 1,2, распределения которых задаются вероятностями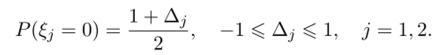

Тогда для суммы случайных величин ?= ?i + ?2 € Z2 справедливо равенство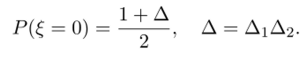

Доказательство. Справедливость утверждения вытекает из равенства.

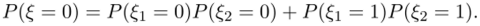
Отсюда при |Д^| < 1 получаем: |Д| < |Д_у|, j = 1,2. Таким образом, суммирование двоичных случайных величин приближает к равномерно распределенной случайной величине. Вместе с тем, если ни одна из исходных двоичных случайных величин не является равномерно распределенной, то их сумма также не будет равномерно распределенной случайной величиной.

Определение 5.23. С каждой случайной величиной у, заданной на группе Z_m и имеющей распределение Р_п = {p_v{i), г € Z_m}, свяжем характеристический многочлен

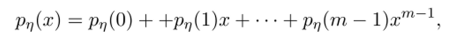
который будем рассматривать как элемент кольца Ж[х/х^т -I многочленов над полем действительных чисел Ш по модулю многочлена х^т — 1.

Кольцо R/x^m — 1 состоит из многочленов f (x) с действительными коэффициентами степени deg (/) < га. Результат сложения (умножения) многочленов g, h е М[ж]/ж^т — 1 есть остаток от деления их суммы (произведения) на многочлен х^гп — 1.

Утверждение 5.19. Пусть р^(х) G М[ж]/ж^т — 1 — характеристические многочлены взаимно независимых случайных величин? j, j = 1,2,…, t и у = YL= €jТогда в кольце М[ж]/ж^т — 1 выполнено равенство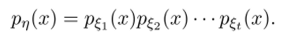

Доказательство, проводится индукцией по t. При t = 2 утверждение вытекает из следующего равенства:

Для практических приложений особый интерес имеет случай, когда сумма независимых случайных величин является равномерно распределенной случайной величиной. Непосредственно из предыдущего утверждения получаем следующее.

Утверждение 5.20. Сумма? = Хд₌₁ & независимых случайных величин С G Z_m, г = 1,2, …Д является равномерно распределенной случайной величиной тогда и только тогда, когда в кольце М[ж]/ж^т — 1 выполнено соотношение

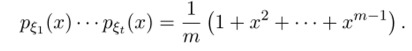
Теорема 5.12. Пусть

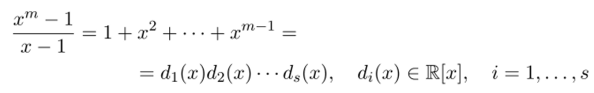
разложение многочлена на неприводимые множители над полем М. Сумма? = Хл=1 ii независимых случайных величин С е Z_m, г — 1, t является равномерно распределенной случайной величиной тогда и только тогда, когда для любого индекса i € {1,2,…, s} найдется индекс j G {1,2,…, t}, при которомр^(х) = 0 (moddj (x)).

Доказательство. Учитывая, что х^т — 1 = (ж —1)(1 + ж²-|——-Ьж^т₁).

и у многочлена х^т — 1 нет кратных корней, в условиях теоремы кольцо К[ж]/ж^т — 1 изоморфно прямой сумме полей.

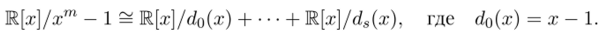
Элементу h (x) е Щж]/ж'^т —1 при данном изоморфизме соответствует вектор h = (го (ж), г₁(.'г),…, г,(ж)), коэффициенты которого удовлетворяют сравнению Vj (x) = h (x) (mod dj (x)). При этом, если h есть характеристический многочлен некоторой случайной величины, то г о (ж) = 1. Следовательно, образом многочлена

являющегося характеристическим многочленом равномерно распределенной случайной величины, будет вектор (1,0,…, 0). Пусть.

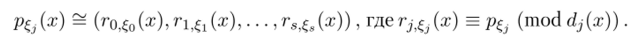
Тогда характеристический многочлен суммы? = ?Т₌₁& будет соответствовать вектору

где.

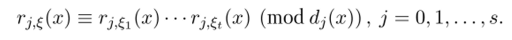
Отсюда, если выполнены условия теоремы, то р${х) = (1,0,…, 0). Следовательно,? — равномерно распределенная случайная величина и достаточность условий доказана. Необходимость условий теоремы вытекает из равенств.

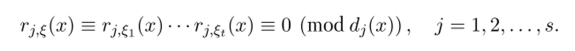
Следствие 1. Пусть 2 ^ т ^ 3. Сумма ? = ^_г=1 С: независимых случайных величин С € Z_m является равномерно распределенной случайной величиной тогда и только тогда, когда найдется индекс j G {1,2,…, t}, при котором — равномерно распределенная случайная величина.

Данный результат следует из неприводимости двух многочленов 1 + ж и 1 + ж + ж² над полем действительных чисел R.

Следствие 2. Пусть т = р — простое число,, …,?₍ & Z_m — независимые случайные величины, у которых все коэффициенты характеристических многочленов являются рациональными числами. Тогда сумма? = Хл₌₁ & есть равномерно распределенная случайная величина тогда и только тогда, когда найдется индекс j € {1,2,… Д}, при котором — равномерно распределенная случайная величина.

Данный результат вытекает из того факта, что многочлен х^р — 1 над полем рациональных чисел имеет только два неприводимых делителя: ж—1 и 1 + ж + • • • + ж^р- см. [2, стр. 59, упр. 9|.