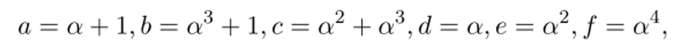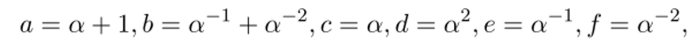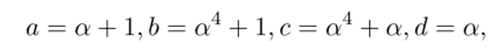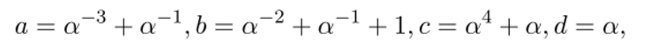Примеры MDS-матриц A8х8 над полем F28

В алгоритме шифрования FOX 128 используется матрица следующей структуры.

Такого сорта матрица имеет v (A) = 21 единицу и с (А) = 6 различных, отличных от нуля элементов, что близко к оптимальным значениям гц (8,8) = 24, (8,8) = 5.

Примерами выбора элементов, приводящих к MDS-матрице, являются:

где а — корень неприводимого многочлена f (x) = l+x²+x^s+x⁴+x^s, f (x) G F2 [ж], а также.

где a — корень неприводимого многочлена f (x) = 1 + ж³ + х^л + x°+ +x⁶ + x⁷ + x^s, f (x) G F₂[x].

Известны примеры MDS-матриц A$_x$ над полем F₂s с оптимальным значением параметра с (А) = с (8,8) = 5:

Матрицы данного вида имеют 15 единичных элементов, что заметно ниже оптимального значения гц (8,8) = 24.

Примерами выбора элементов, приводящих к MDS-матрице, являются:

где а — корень неприводимого многочлена f (x) = 1+ж²+ж³+ж⁴+ж⁸, /(ж) G Р₂[ж], а также.

где а — корень неприводимого многочлена /(ж) = 1 + ж³ + ж⁴ + ж⁵+ +ж⁶ + х⁷ + X^s, /(ж) G F₂[ж].

В заключение главы приведем алгоритм проверки того, что заданная d х d матрица А = (ау) над полем F₂n является MDSматрицей. Мы будем основываться на сформулированном нами ранее утверждении 5.24.

Алгоритм 5.1 (Проверка MDS-матрицы) Вход: п > 1, неприводимый многочлен /(ж) степени п, /(ж) € F-2[x], матрица А = («;,-) размера d х <7 с коэффициентами из поля F₂».

Выход: двоичная переменная b_rnds, принимающая значение true, если А = (a-ij) — MDS матрица, и b_mds = false — в противном случае.

• 1. Определяем b_mds = true.
• 2. Вычисляем обратную матрицу Л^-1. Если обратной матрицы не существует, полагаем b_mds = false и завершаем алгоритм.
• 3. Проверяем, что все d² элементов матриц А и Л^-1 отличны от нуля. Если это не так, то полагаем b_rnds = false и завершаем алгоритм.
• 4. Если d < 3, то завершаем алгоритм со значением b_mds = true.
• 5. Определить t = d — 2.
• 6. Пока t > 1 и b_mds = true, выполнять
• 6.1. Перечисляем все множество ^ ^ ^ подматриц размера t х t в массив L.
• 6.2. Для всех е от 0 до ^ ^ ^ - 1 выполнить:
• 6.2.1. Вычисляем обратную матрицу к матрице L[e] и поместим ее по адресу М[е.
• 6.2.2. Если обратная матрица М[е] не существует или один из ее элементов равен нулю, то полагаем b_rnds = false и завершаем алгоритм.
• 6.3. Определить t = t — 2.
• 7. Вернуть значение b_mds в качестве выхода алгоритма. ?