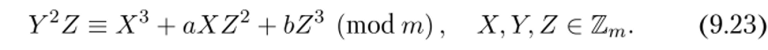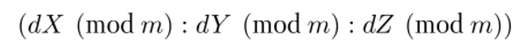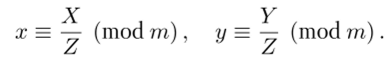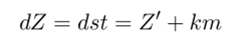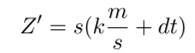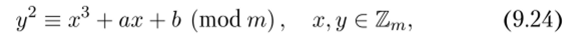Эллиптические кривые над кольцами

Выше мы рассмотрели уравнения (9.11), (9.12) над произвольным полем К и определили на множестве их решений структуру абелевой группы — группы точек эллиптической кривой. Однако мы можем рассмотреть эти уравнения над произвольным кольцом, например кольцом вычетов Ъ_т по модулю некоторого натурального составного числа га. Рассмотрим сравнение.

Пусть (X: Y: Z) — произвольная тройка, удовлетворяющая сравнению (9.23), тогда для любого d Е Ъ_т такого, что НОД (d, m) = 1, тройка.

также является решением сравнения (9.23). Этот факт позволяет нам задать на таких тройках отношение эквивалентности

Множество эквивалентных троек мы, как и ранее, будем называть точкой, а множество точек — эллиптической кривой ?_a,&(Z_m), определенной над кольцом Z_m в проективной форме записи.

Следует заметить, что множество точек эллиптической кривой ?а, ь (%т) не образует абелеву группу, однако для нее можно рассмотреть отображения, заданные равенствами (9.18) и (9.19), рассматриваемыми как сравнения в кольце Z_m. Результат применения указанных отображений также принадлежит множеству ?_aj,(Z_m).

Предположим, что для некоторого представителя (X: Y: Z) точки кривой ?_а, ь (Z_m) выполнено условие НОД (2', т) = 1, тогда мы можем аналогично равенствам (9.14) определить аффинную точку (х, xj)

Если же у точки кривой есть представитель (X: Y: Z) такой, что НОД (?, т) = s > 1, то вычет Z ¹ (modm) не может быть определен.

Обозначим Z = st. Тогда для любого взаимно простого с т вычета d также будет выполнено.

для некоторого целого к и t = у. Следовательно, величина.

является целым числом, для которого НОД (Z'- m) ^ s > 1. Мы получили, что если Z-координата хотя бы одного представителя точки кривой не является взаимно простой с т, то и Z-координаты всех остальных представителей также не взаимно просты с т и, следовательно, не могут быть приведены к аффинной форме записи.

Рассмотрим теперь сравнение.

определяющее эллиптическую кривую ?_0if,(Z_m) в аффинной форме записи.

Легко видеть, что каждой точке (х, у), удовлетворяющей сравнению (9.23), найдется тройка (х: у : 1), удовлетворяющая (9.24). Обратное, как следует из сказанного выше, неверно.

Как мы покажем далее, этот факт может быть существенно использован при разложении числа m на множители, см. главу 13. Другие приложения эллиптических кривых, определенных над кольцом вычетов Z_m, мы приведем в следующих главах.