«N — 1» методы доказательства простоты

Теперь мы перейдем к рассмотрению методов, позволяющих получить строгое доказательство простоты числа. Именно подобный класс методов используется на практике при построении простых чисел, используемых в криптографических схемах.

Методы доказательства простоты целых чисел, использующие разложение числа т — 1 на простые множители, были известны достаточно давно. Хорошо известна теорема Эдуарда Люка (Edouard Lucas) о простоте числа гп, основанная на свойствах первообразных корней.

Теорема 13.2 (Люка, 1876). Пусть т > 1 — нечетное целое число. Если найдется целое число а, НОД (а, т) = 1, такое, что для любого простого делителя q числа т — 1 выполнены сравнения

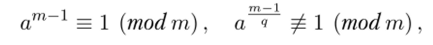
то т — простое число.

Основываясь на теореме Люка, мы можем предложить простой тест проверки простоты нечетного числа т, если известно разложение rn — 1 на множители.

Алгоритм 13.3 (Алгоритм Люка доказательства простоты).

Вход: Целое число га такое, что га — 1 = шис;

Выход: Заключение о том, является число га простым или составным.

• 1. Определить с = 20 и к = 1.
• 2. Выбрать случайно элемент 1 ^ а < т. Если НОД (а, т) > 1, то закончить алгоритм с уведомлением, что число га составное.
• 3. Вычислить с = с — 1. Если с = 0, то завершить алгоритм с уведомлением, что алгоритм не может дать однозначного ответа на вопрос, составное число или нет.
• 4. Выполнять, пока к ^ п
• 4.1. Если а^т~¹ ^ 1 (mod га), то число га составное.

ГО — 1.

4.2. Если выполнено условие а ** =1 (mod m), то вернуться на шаг 2.

• 5. Вычислить fc = к + 1.
• 6. Завершить алгоритм с уведомлением, что число га простое. ?

Ситуация, когда нам полностью известно разложение числа га — 1 на простые множители, возникает нечасто. Как правило, используемые нами методы разложения на множители позволяют получить лишь частичное разложение числа га — 1 на множители. Это вынуждает нас использовать более тонкие результаты, чем теорема Люка.

Итак, мы хотим проверить на простоту нечетное натуральное число га. Запишем га — 1 в виде.

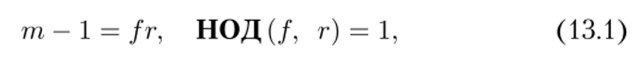
где / - число с известным разложением на множители / = П?₌₁ Qk^k, а г — составное число с неизвестным разложением на множители. Заметим, что если число г простое, то мы получаем полное разложение числа га — 1 на простые сомножители, что позволяет нам воспользоваться теоремой Люка для проверки простоты га. Поэтому далее будем считать, что число г составное.

Дополнительно мы будем считать, что каждый простой делитель q числа г удовлетворяет неравенству q > В для некоторого натурального числа В. В качестве границы В на практике можно выбрать величину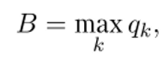

то есть максимальное из простых чисел, входящих в разложение числа /. Впрочем, можно несколько увеличить эту границу, взяв в качестве величины В значение <7^+1 — 1, где qx*+i «следующее за максимальным % простое число.

Определим следующие условия.

1. Для каждого простого числа </*, к = 1, п, входящего в разложение числа /, найдется некоторое взаимно простое с т целое число a& такое, что.

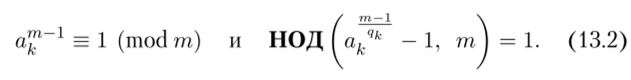
2. Найдется некоторое взаимно простое с тп целое число Ь такое, что.

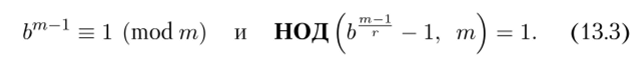
Выполнимость одного или двух указанных условий позволяет нам говорить о простоте числа тп.

Теорема 13.3 (Поклингтон, 1918). Рассмотрим нечетное натуральное число т, удовлетворяющее условию (13.2). Пусть р — произвольный простой делитель числа т, тогда

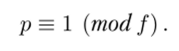
Сформулированная теорема была впоследствии использована Дерриком Лемером (Derrick Henry Lehmer) для доказательства простоты целых чисел.

Теорема 13.4 (Лсмср, 1927). Пусть т > 0 — нечетное целое число. Если число т удовлетворяет условию теоремы 133 и /² ^ Дт, то число т — простое.

Доказательство. Если выполнены условия теоремы 13.3, то для любого простого делителя р числа т выполнено равенство р = 1 + kf при некотором к € Z. Следовательно, для любого простого делителя р выполнено неравенство p=l + kf^l + Дт > Дт, которое противоречит утверждению леммы 9.1. Полученное противоречие завершает доказательство. ?

Приведем пример использования данной теоремы. Рассмотрим число m = 156 • 5²⁰² + 1. Используя вычисления на ЭВМ, находим, что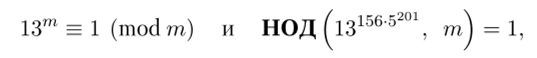

следовательно, всякий простой делитель р числа тп имеет вид р — 1 + А'5²⁰². Поскольку 5²⁰² > Дтп, то число тп простое.

Теперь покажем, как можно использовать для доказательства простоты введенное нами ранее условие (13.3).

Теорема 13.5. Пусть т — нечетное натуральное число, для которого выполнено условие (13.3) и р — произвольный простой делитель числа т, тогда

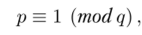
где q — некоторый простой делитель числа г.

Скомбинировав утверждения двух последних теорем, можно получить следующее утверждение.

Теорема 13.6. Пусть т — нечетное натуральное число, для которого выполнены условия (13.2) и (13.3). Пусть р — произвольный простой делитель числа т, тогда

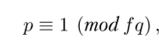
где q некоторый простой делитель числа г. Кроме того, если выполнено неравенство

то т — простое число.

Доказательство данной теоремы очевидным образом основывается на утверждениях предыдущих теорем, и мы предлагаем его читателю в качестве упражнения.

Основываясь на изложенных выше идеях, приведем несколько алгоритмов построения простых чисел, которые используются при генерации параметров криптографических схем.

Далее мы приведем простой рекурсивный алгоритм, который позволяет строить простые числа р с известным разложением числа р— 1 на множители. Основная идея данного алгоритма заключается в поиске простых чисел в арифметических прогрессиях. Хорошо известен следующий результат.

Теорема 13.7 (Дирихле, см. [2, гл. 3]). Пусть арифметическая прогрессия задана соотношением :гд. — ak+b, к — 0, 1, …, где параметры а, Ь — натуральные взаимно простые числа. Тогда среди чисел ац- бесконечно много простых.

Как показывают практические вычисления, простые числа встречаются в арифметических прогрессиях достаточно часто. В комбинации с изложенными выше теоремами Поклингтона и Лемера мы получаем достаточно удобный инструмент для построения больших простых чисел.