Кинематический анализ пространственных расчетных схем

Необходимое условие геометрической неизменяемости. Рассмотрим пространственную расчетную схему, состоящую из Т тел. Каждое тело, взятое отдельно, имеет в пространстве шесть степеней свободы (см. рис. 1.1,.

а). Пока тела не соединены между собой, совокупная степень их свободы будет равна 6 Т. Простой шаровой шарнир, соединяющий два тела, уничтожает три степени свободы. Если в расчетной схеме имеются тела, жестко соединенные друг с другом, то жесткое соединение этих тел уничтожает по шесть степеней свободы. Кроме того, по одной степени свободы уничтожает каждая простая линейная связь.

Тогда степень свободы анализируемой расчетной схемы будет.

где Т — число тел; С — число простых линейных связей во всех соединениях тел; Ж — число жестких соединений тел; С_оп — число опорных связей.

Если в расчетной схеме отсутствуют жесткие соединения тел, формула (1.7) принимает вид Если для данной расчетной схемы W> 0, система изменяема; если W = 0, система неизменяема; если W < 0, система неизменяема, но имеет избыточные связи, не требуемые для обеспечения геометрической неизменяемости.

Таким образом, для обеспечения геометрической неизменяемости необходимо выполнение условия.

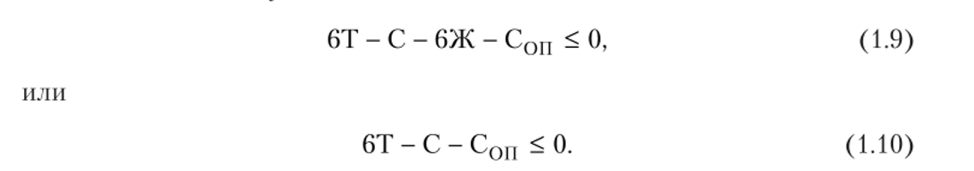
Формулы (1.7) и (1.8) и соответствующие им условия (1.9) и (1.10) описывают общий случай определения степени свободы пространственной расчетной схемы.

При анализе пространственных ферм удобнее пользоваться иными, более простыми зависимостями.

Обозначим число узлов пространственной фермы через У, число собственных стержней фермы через С_ф, число опорных стержней через С_оп.

Каждый узел фермы можно рассматривать как точку, которая в свободном состоянии имеет три степени свободы. Таким образом, степень свободы необъединенных между собой узлов будет равна ЗУ. При соединении двух узлов стержнем суммарная степень свободы уменьшается на единицу. Следовательно, стержень фермы можно рассматривать как простую линейную связь. Полное число связей фермы, ограничивающих степень свободы ее узлов, будет равно С_ф + С_оп. Тогда степень свободы пространственной фермы может быть определена как.

а необходимое условие геометрической неизменяемости примет вид.

Соблюдение условий (1.9), (1.10) и (1.12) необходимо, но недостаточно, так как указанные соотношения устанавливают необходимые соотношения между числом связей и числом тел, но не показывают, как же соединены эти тела между собой. Достаточность указанных условий должна быть дополнена анализом геометрической структуры расчетной схемы.

Анализ геометрической структуры. Анализ геометрической структуры расчетной схемы базируется на правилах соединения тел в единое жесткое целое и присоединения их к основанию.

Для образования неизменяемого соединения двух тел или присоединения одного тела (неизменяемой группы тел) необходимо не менее шести простых линейных связей. Задача состоит в том, как расположить эти стержни, так как их неправильное размещение повлечет за собой изменяемость соединения.

На рис. 1.22 показаны примеры неправильного присоединения к основанию неизменяемой системы тел или соединений двух тел.

Рассмотрим исключительные соединения двух тел при помощи шести линейных связей, приводящие к мгновенной изменяемости.

• 1. Оси шести линейных связей пересекают одну прямую, А А (рис. 1.22, а). Эта прямая будет осью бесконечно малого поворота одного тела относительно другого. Здесь могут быть следующие частные случаи:
  • — линейные связи по три пересекаются в двух точках (рис. 1.22, б). Через эти точки проходит прямая А — А, являющаяся осью бесконечно малого поворота двух соединяемых тел;
  • — четыре линейные связи расположены в одной плоскости (рис. 1.22, в). В этом случае две другие линейные связи пересекут эту плоскость в двух точках, через которые проходит прямая, пересекаемая осями всех четырех стержней, лежащих в указанной плоскости. Прямая А — А будет осью бесконечно малого поворота двух соединяемых тел;
  • — линейные связи расположены в параллельных плоскостях (рис. 1.22, г). Точки пересечения осей связей в силу параллельности плоскостей будут иметь одновременное бесконечно малое смещение в направлении, перпендикулярном плоскостям (по линиям смещения I, II и III, показанным на рисунке);
  • — линейные связи расположены в двух плоскостях (рис. 1.22, д). Прямая пересечения плоскостей А — А пересекается осями всех стержней и является осью бесконечно малого поворота соединяемых тел.

Рис. 1.22

• 2. Более трех осей линейных связей пересекаются в одной точке:
  • — оси линейных связей параллельны (рис. 1.22, е). Если в соединении есть более трех линейных связей, оси которых параллельны, соединяемые тела могут иметь поступательные перемещения относительно друг друга, но любому направлению в плоскости, перпендикулярной осям связей (или бесконечно малый поворот вокруг оси А — А)

оси линейных связей не параллельны, но более трех из них сходятся в одной точке. Сходящиеся связи закрепляют только три степени свободы. Остальных связей (менее трех) недостаточно для закрепления еще трех степеней свободы.

3. Оси трех линейных связей лежат в одной плоскости и сходятся в одной точке (рис. 1.22, ж). Сходящиеся связи в этом случае закрепляют всего две степени свободы. Остальных связей недостаточно, чтобы закрепить остальные четыре степени свободы соединяемых тел.

Примеры правильного расположения связей при прикреплении пространственных тел к основанию показаны на рис. 1.23.

Рассмотрим несколько примеров анализа геометрической структуры пространственных расчетных схем.

Рис. 1.23.

Пример 1.4

Произвести проверку геометрической неизменяемости прикрепления твердого тела к основанию (рис. 1.23, Э).

Решение. Количество тел Т= 1, количество опорных связей С_оп = 6. Необходимое условие геометрической неизменяемости (1.8) выполняется, так как 1^=6 -1−6 = 0.

Анализ прикрепления тела к основанию начинаем с определения заведомо неподвижной точки тела. Такой точкой является точка F, прикрепленная к основанию тремя связями ЛЕ, BF и CF, не параллельными и не лежащими в одной плоскости. Следующая неподвижная точка — Е, также закрепленная по трем направлениям: двумя связями АЕ и DE — с основанием, и самим телом Т по линии EF с неподвижной точкой F. Таким образом, две точки тела Fw Е прикреплены неподвижно.

Свободу перемещений остальных точек тела ограничивает связь CG, поставленная вертикально, так как ось этой связи не должна проходить через прямую EF (пересекаемую всеми остальными стержнями) или быть параллельной. В противном случае возможен бесконечно малый поворот тела Т вокруг прямой EF.

Следовательно, рассматриваемое прикрепление твердого тела к основанию геометрически неизменяемо.

Аналогично анализируются и другие способы прикрепления тела к основанию, представленные на рис. 1.23.

Пример 1.5.

Проверить геометрическую неизменяемость пространственной рамы, изображенной на рис. 1.24.

Рис. 1.24.

Решение. В рассматриваемой расчетной схеме пространственной фермы общее число узлов У = 8; число стержней фермы С_ф= 16; число опорных связей С₀п = 8. Необходимое условие геометрической неизменяемости (1.12) выполняется:

1У = 3 • 8 — 16 — 8 = 0.

Анализ соединения стержней фермы начинаем с определения ее неподвижных частей. Неподвижной точкой опорного кольца является узел А, закрепленный опорными стержнями в трех направлениях. Тогда стержни опорного кольца АВ, ВС, CD и DA тоже будут неподвижными, так как каждый узел кольца будет закреплен в трех направлениях: непосредственно опорными стержнями в двух направлениях и через стержень опорного кольца на соседней опоре в другом направлении.

Каждый последующий узел фермы прикреплен к неподвижным узлам опорного кольца тремя связями, стержнями фермы, не параллельными и не сходящимися в одной точке, и поэтому также является неподвижным.

Таким образом, вся ферма является геометрически неизменяемой.