Действие ударной нагрузки

При ударе происходит передача кинетической энергии ударяющего груза упругой системе, сопровождающаяся деформацией последней и возникновением равных между собой сил взаимодействия груза и упругой системы. Удар может быть продольным, если ударяющий груз действует вдоль оси элемента расчетной схемы, и поперечным, если удар происходит перпендикулярно оси элемента.

Рассмотрим явление удара при следующих допущениях:

• 1) при ударе в элементе расчетной схемы возникают только упругие деформации;
• 2) удар считается неупругим, т. е. ударяющее тело не отскакивает после удара, а продолжает перемещаться вместе с ударяемым телом как одно целое.

Предположим, что груз весом G падает на невесомую балку с высоты h. Скорость падения груза, как известно из курса физики, равна v = s]2gh, откуда h = v² /2g.

Действие ударяющего груза на балку выразим через эквивалентную силу Р_жв. Очевидно, что тогда динамическое перемещение места удара будет у_тш = 8_ПР_жв, где 6_И — податливость балки в направлении удара.

Выразим эквивалентную силу через динамическое перемещение: Р_жв = — Удин / ^ii;

Пол пая работа падающего груза Т_у = G (h + у_лпп).

Полученная работа переходит в потенциальную энергию деформации ударяемой конструкции:

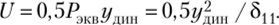
Приравняв на основании формул (12.14) и (12.15) Т_у = U, получим.

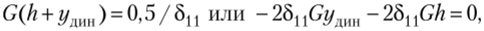
где 6_nG = A_1G — статический прогиб места удара от статического действия груза G.

Решив полученное квадратное уравнение относительно у_тн, получим.

Выражение в скобках формулы (15.32) показывает, во сколько раз результат ударного (динамического) действия груза больше его статического действия, и, следовательно, является динамическим коэффициентом при ударе, т. е.

Таким образом, Р_экв = р G, у_ши = рД₁₀. Эти же соотношения между статическим и динамическим действием падающего груза в силу допущения о справедливости закона Гука в пределах упругости сохраняются для любых усилий, напряжений и перемещений в сечениях расчетной схемы.

Определив силу удара Р_экв, можно производить обычный статический расчет любой расчетной схемы, считая Р_экв обычной статической нагрузкой.

Если в формуле (15.33) h — 0, т. е. нагрузка приложена сразу (случай внезапного приложения нагрузки), величина динамического коэффициента р = 2. Это означает, что внезапно приложенная нагрузка вызывает вдвое большие деформации и напряжения, чем статическое действие той же нагрузки.

При наличии на сооружении в месте удара сосредоточенной массы т при массе падающего груза т_л статический прогиб от веса обеих масс будет уже равным.

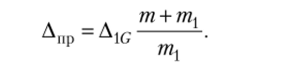
Подставляя в формулу (15.33) Д_пр вместо Д_1С, получим.

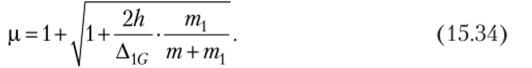
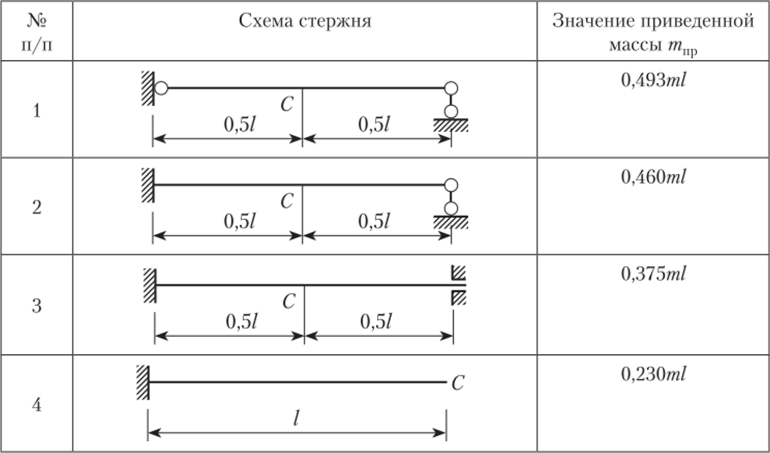
Равномерно распределенная масса т (т/м) конструкции приводится к сосредоточенной в месте удара. В табл. 15.2 приведены значения массы т_пр при приведении распределенной массы к месту удара С.

Таблица 15.2

Приведение равномерно распределенной массы к месту удара.

Пример 15.6.

Требуется определить силу удара груза G_i = 2 кН, падающего с высоты h = 0,2 м на железобетонную балку (рис. 15.15) с пролетом / = 6,0 м. Балка изготовлена из бетона класса ВЗО (Е_ь = 32,5 • 10³ МПа, 1_г = 36 • 10~⁴ м⁴). Собственный вес балки G = 20 кН. Решение. 1. Масса падающего груза т_{ = G_x / g = 2 / 9,81 = 0,204 т.

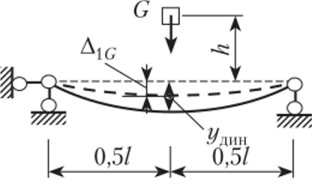
Рис. 15.15.

2. Масса балки, приведенная к месту удара (табл. 15.2, п. 1) т_пр = 0,493G / g = 0,493 • 20 / 9,81 = 1,005 т.

Статический прогиб от действия падающего груза (см. рис. 10.7).

GP 2 б³

А_1С = -т = 7,69−10″ ⁵ м.

48?/ 48−32,5*10⁶ -36 10″⁴

Соотношения масс т_х / (т_{ +т) = 0,204 / (0,204 + 1,005) = 0,1687.

Значение динамического коэффициента [см. формулу (15.34) |.

I 20 2.

ц = 1 + ₄ 1 + - - ' - 0,1687=30,64.

V 7,69 Ю" ⁵

Эквивалентная сила удара Р_жп= = 30,64 • 2 = 61,28 кН.

Пренебрегая собственной массой балки, получим динамический коэффициент [см. формулу (15.33)] и силу удара значительно большие:

р = 1+ J1+ ^{2 0,2}, = 73,13; = 73,13• 2 = 146,26 кН.

V 7,6910-⁵

Таким образом, сила удара груза, даже при падении с небольшой высоты, оказывается значительно больше, чем вес самого груза, причем, как видно из формул (15.33) и (15.34), сила удара увеличивается с увеличением жесткости сооружения.

Пример 15.7.

При забивке деревянной сваи d = 0,2 м, длиной /= 6,5 м (рис. 15.16) молот копра весом G = 1,6 кН падает с высоты h = 0,6 м. Определить динамические напряжения в сечениях сваи, условно принимая, что нижнее сечение не смещается. Модуль упругости для древесины вдоль волокон ?=0,1 • 10⁵ МПа.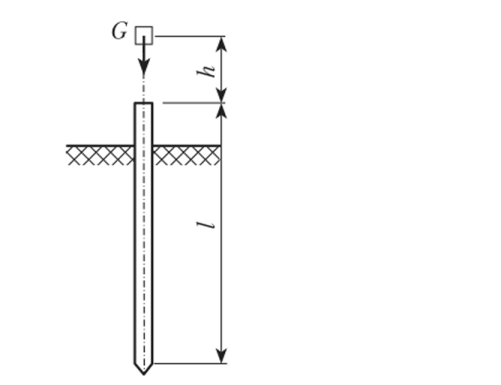

Рис. 15.16

Решение. 1. Площадь поперечного сечения сваи А = пг² = я • 11² = 380,133 см².

• 2. Жесткость сваи при сжатии ЕЛ = 0,1 • 10⁸— 380,133 • 10~⁴ = 380 133 кН.
• 3. Продольное статическое укорочение сваи

_А GI 1,6 6,5.

Д_|Г= — = —-—=27,36 Ю^-6 м.

• 1С ЕЛ 380 133
• 4. Динамический коэффициент [см. формулу (15.33) |

n = l + jl+—^{2 0,6} =210,43.

^h V 27,36−10-е.

5. Статическое напряжение в свае а_с= G/A = 1,6 / 380,133 • 1(Н = 42,09 кН/м².

6. Динамическое напряжение а_дии = ра_с= 210,43 • 42,09 = 8857 кН/м² = 8,857 МПа.