Способ приведенных масс

Назначение способа — свести систему со многими степенями свободы к системе с меньшим числом степеней свободы или даже к системе с одной степенью свободы. Эта операция выполняется на основе равенства количества кинетической энергии систем с различным числом степеней свободы.

При замене распределенной массы, как и в энергетическом методе, необходимо знать форму колебаний. Примем ее, как и в гл. 3, в виде произведения двух функций: у (х, t) = y (x)f (t). Взяв производную по времени от этой функции, получим выражение для скорости:

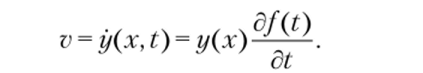
Зная скорость, можно записать выражение кинетической энергии для распределенной массы т (х):

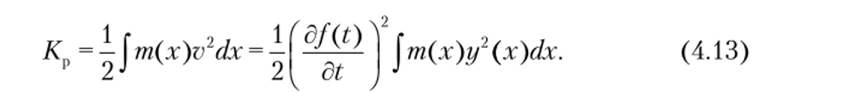
Рассмотрим теперь ту же систему, но с одной степенью свободы, сосредоточив массу т₁ в определенной точке конструкции, которую обозначим через 1. Ордината в точке 1 будет определяться выражением у (х, t) = yj{t), где г/, — амплитуда колебаний точки приложения сосредоточенной массы т_л. Скорость колебаний этой точки имеет вид.

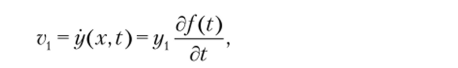
а кинетическая энергия будет представлена выражением.

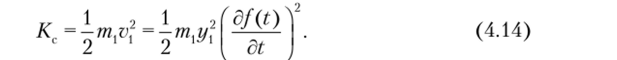
Из равенств выражений (4.13) и (4.14) определим искомую массу:

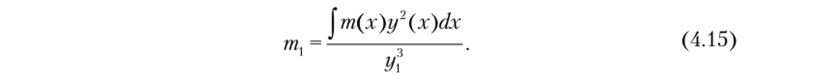
Поскольку истинная форма колебаний у (х) неизвестна, то ее нужно задавать с учетом граничных условий. Отсюда приближенность рассматриваемого способа. Другое затруднение — выбор места приложения массы. Очевидно, что целесообразно точку приложения массы назначать в месте наибольшего отклонения кривой от недеформированной оси стержня. Функцию у (х) удобно представлять через г/, тогда это значение сокращается в выражении (4.15). После определения приведенной массы дальнейший расчет выполняется как для системы с одной степенью свободы (см. гл. 1).

Пример 4.4. Определим низшую частоту свободных колебаний шарнирно опертой бачки постоянного сечения с равномерно распределенной массой т. Приведенную массу поместим в середине пролета. Форму колебаний примем по синусоиде: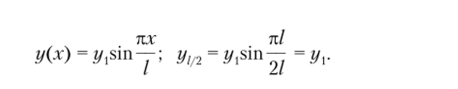

Решение

Подставим значения формы колебаний в формулу (4.15):

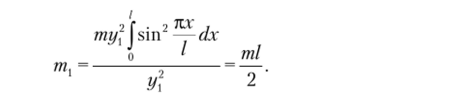
Получили тот же самый результат, что и при замене распределенной массы сосредо точенной массой, но правилу рычага. Определим частоту свободных колебаний по формуле (1.4):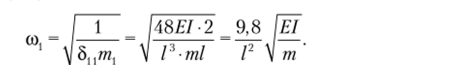

/³

Прогиб в середине пролета от единичной силы: 8″ = ?

Расхождение составляет 0,7%.

Упражнение 4.5. Решите пример 4.1 способом приведенных масс. Приведенную массу поместите па конце консоли. Форму колебаний примите, как в примере 4.1.

В ряде случаев возникает необходимость понижения числа степеней свободы системы. Эту операцию легко выполнить способом приведенных масс. Пусть имеется система с п степенями свободы. Требуется понизить число степеней свободы до k, где k < п. При сосредоточенных массах в том и другом случае в качестве формы колебаний можно взять собственные векторы, определяемые, например, с помощью системы MATLAB. Уравнения для вычисления приведенных масс М- будут иметь вид.

Здесь т- — заданные сосредоточенные массы; y_i и у_} — соответственно перемещения масс M_i и т₎ (берутся из заданной формы колебаний).

Пример 4.5. Пусть имеется расчетная схема десятиэтажного здания в виде консольного стержня (рис. 4.7, а). Исходные данные: т_л = т₂ = т₃ = т_л = т₅ = т_в = = т₁ = тп_ь= т₉ = 510 г, т_п) =615 т. Высота всех этажей одинакова: h = 3,3 м. Жесткость EI = 718 015 680 кН м². Заменим заданную расчетную схему системой с тремя степенями свободы, разместив приведенные массы на уровне 3, б и 9-го этажей (рис. 4.7, б).

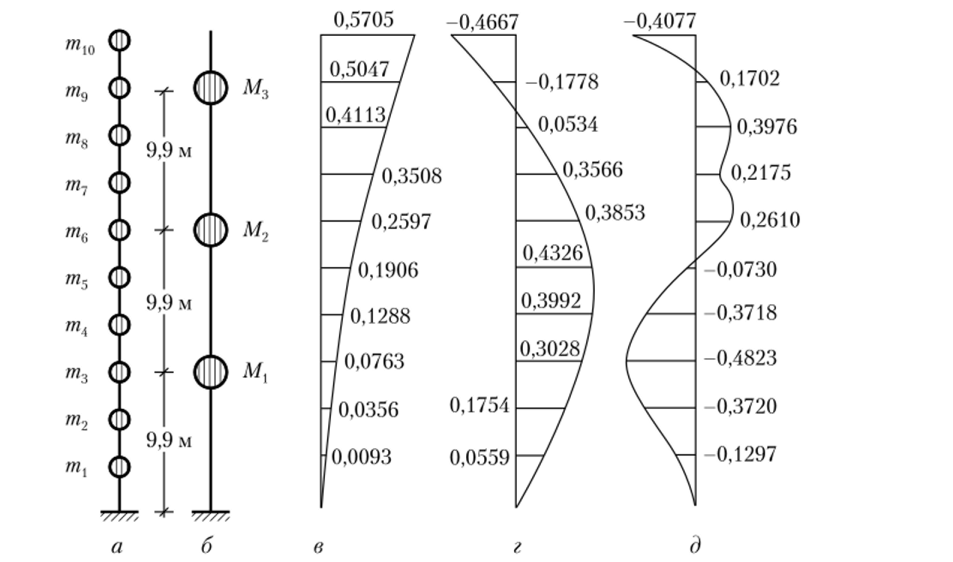
Рис. 4.7. Формы колебаний системы с 10 степенями свободы.

Подсчитаем частоты собственных колебаний и соответствующие им векторы, например с помощью системы MATLAB (см. приложение 1.1).

Решение

В данном случае система статически определимая, поэтому нужно составить только матрицы b, f и М. Собственные векторы для первых трех частот (со, = 6,0 с^-1; со₂= 38,0 с^-1; со₃= 117,8 с^-1) приведены на рис. 4.6, в — д.

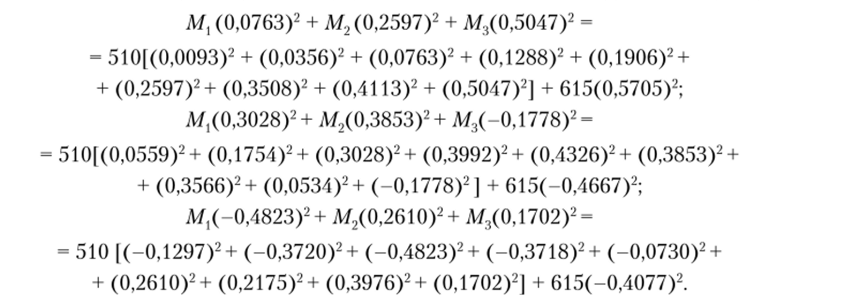
В результате решения системы уравнений получим, что = 1375 т, М₂ = 2428 т, М₃ = 1462 т.

Для системы с этими массами (рис. 4.6, б) подсчитаем частоты: со, = 6,16 с ¹ (+2,6%); со₂= 38,42 с ¹ (+1,1%); со₃ = 111,06 с ¹ (-5,7%). В скобках указан процент расхождения с частотами, полученными выше.

В заключение еще раз отметим, что точность вычислений зависит от удачного расположения приведенных масс. Поэтому в некоторых случаях необходимо сделать несколько попыток.