Решение задач устойчивости методом Бубнова — Галёркина

Метод впервые был применен И. Г. Бубновым (1913 г.) и затем Б. Г. Галёркиным (1915 г.). Метод использовался для приближенного решения дифференциальных уравнений, не связанных с вариационными проблемами [20].

Исходным пунктом в методе является дифференциальное уравнение изогнутой оси стержня. В общем случае, когда стержень имеет переменное поперечное сечение, переменную по длине продольную силу, в момент потери устойчивости уравнение примет вид Это уравнение можно получить из рассмотрения равновесия бесконечно малого элемента оси стержня в слегка изогнутом состоянии. Уравнение в развернутом состоянии записывается следующим образом:

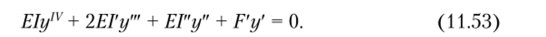
Если EI и F имеют постоянные значения, уравнение упрощается:

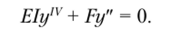
При решении задачи устойчивости стержня от собственного веса при постоянном сечении уравнение примет вид.

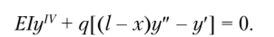
При решении задач методом Бубнова — Галёркина форма потери устойчивости стержня, как и в методе Ритца, задается приближенным выражением в виде ряда (11.50). Но на этот раз функции ф,(.г), ф₂(х),…, ф"(.г) должны удовлетворять всем граничным условиям стержня.

В общем случае решение заключается в следующем: если у (х) является точным решением краевой задачи, то уравнение (11.52) будет равно нулю, и, следовательно, функция, стоящая в левой части этого уравнения, будет ортогональной к любой функции, в том числе и к функциям (11.50), т. е.

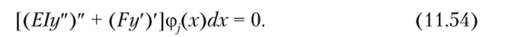
Это и есть уравнение Бубнова — Галёркина.

Однако методу дана и другая трактовка, основанная на принципе возможных перемещений. В качестве возможных перемещений принимаются функции ф₂(д). •••> ф"(-^г)> которые являются кинематически возможными, так как они удовлетворяют всем граничным условиям. Составим уравнение для возможных работ. При этом учтем, что рассматриваемый стержень в отклоненном положении должен находиться в равновесии (статический критерий устойчивости) под действием внутренних и внешних сил. В соответствии с принципом возможных перемещений сумма возможных работ внешних и внутренних сил должна равняться нулю:

Здесь интеграл от первого члена в скобках, умноженного па функцию cfпредставляет работу внутренних сил, а интеграл от второго члена, также умноженного на эту функцию, представляет работу внешних сил. Если для решения задачи берется несколько функций, то для каждой из них составляется равенство (11.55).

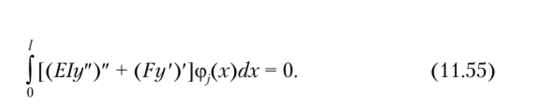
Далее процедура решения напоминает процедуру метода Ритца. После интегрирования получается система однородных линейных алгебраических уравнений относительно параметров й_;. Далее составляется определитель из коэффициентов при а_; и приравнивается к нулю, что дает уравнение устойчивости, из которого определяется критическая нагрузка.

Пример 11.13. Определим критическую нагрузку для стержня, изображен;

(лЛ пого па рис. 11.19, с заданным изменением поперечного сечения I_x = I + ~.

¹)

В качестве формы потери устойчивости примем ряд, удовлетворяющий всем.

ш 2лх

граничным условиям: у (х) = a, sin— + «₂sin-r-.

Рис. 11.19. Стержень переменного сечения.

Решение

Для решения возьмем дифференциальное уравнение (11.53), составленное для случая переменного поперечного сечения. Вычислим производные:

жителя — 14,50. Расхождение — 1,07%.

Выполним второе приближение.

Пропуская подстановку функций в уравнение (11.53), выпишем результат после перемножения и интегрирования:

Составим п раскроем определитель из коэффициентов при В итоге полу;

После умножения на синус, интегрирования и приведения подобных членов получим.

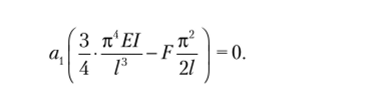
3 л²Е1

Е1

3 п²Е1 Е1

Так как а, Ф 0, то Т_кр = -• = 14,8 —. Точное значение численного мно.

EI (EI)²

чим квадратное уравнение F² — 73,95—F+ 862,34 — =0.

^ V * >

Из уравнения находим наименьший корень, через который определяем крити- EI

ческую нагрузку F_Kp = 14,50 —, что практически совпадает с точным значением.

Упражнение 11.7. Определите критическую силу для стержня постоянного сечения (см. рис. 11.2, а) методом Бубнова — Галёркина, используя кх

функцию у (х) = a, sin—.

Контрольные вопросы

• 1. Какой критерий устойчивости реализуется в энергетическом методе?
• 2. В чем заключается принцип Дирихле?
• 3. Какая энергия реализуется в энергетическом методе?
• 4. Чем нужно задаваться при реализации энергетического метода, и какие при этом должны быть условия?
• 5. В какую сторону дает отклонение энергетический метод при правильном его использовании?
• 6. За счет какого перемещения совершает работу внешняя сила в энергетическом методе?
• 7. Какие усилия, кроме момента, надо учитывать при расчете многоэлементных сетчатых систем?
• 8. Является ли точным метод конечных элементов при решении задач устойчивости?
• 9. В чем отличие метода конечных элементов при решении задач устойчивости от метода перемещений?
• 10. Какое свойство потенциальной энергии реализовано в методе Ритца?
• 11. В чем заключается идея метода Бубнова — Галёркина при решении задач устойчивости?
• 12. В чем отличие расчета на прочность от расчета на устойчивость?