Мощностная нижняя оценка

В работе [86, с. 92] бездоказательно, просто как очевидный факт утверждается, что время поиска по крайней мере не меньше чем время необходимое на перечисление ответа. В нашей модели этот факт находит свое доказательство и носит название мощностной нижней оценки. В связи повсеместностью применимости мощностной нижней оценки часто при оценке времени алгоритма поиска оценивают только разность между временем поиска и временем перечисления ответа (см., например, [64, 86]).

Пусть нам даны произвольные множества запросов X, записей У и отношение поиска р на X х У. Причем на множестве запросов задано вероятностное пространство (X, а, Р).

Скажем, что базовое множество Т допустимо для ЗИП I, если существует ИГ над базовым множеством Т, который разрешает ЗИП I.

Следующий результат, называемый мощностной нижней оценкой, справедлив для любой ЗИП при минимальных ограничениях. Смысл этого результата заключается в том, что время поиска не может быть меньше чем время, необходимое на перечисление ответа.

Справедлива следующая теорема [22].

Теорема 4 (мощностная нижняя оценка). Пусть I = = (X, У, р) — произвольная ЗИП, такая, что существует такая запись у G V, что 0(у, р) ф 0, Т — измеримое базовое множество, допустимое для I, тогда

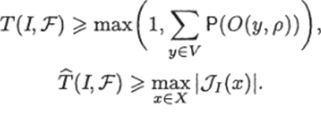
Доказательство. Возьмем произвольный ИГ ?/, разрешающий задачу I. Такой граф существует, так как U (I, T) ф 0.

Возьмем произвольный запрос х € X. Так как ИГ U разрешает ЗИП /, то ответ на запрос х

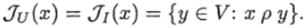
Возьмем произвольную запись у 6 Ju (х). Поскольку запись у попала в ответ, то, значит, в ИГ U существует некий лист а, которому приписана запись у и такой, что <�р_а(х) = 1. А так как ip_Q(x) = 1 и никакой лист не совпадает с корнем, то существует цепь, ведущая из корня в лист а, проводимость которой равна 1, и в этой цепи есть ребро, ведущее в а, с проводимостью 1. Это ребро назовем проводящим ребром записи у. Понятно, что разным записям из Ju{%) соответствуют разные проводящие ребра, так как эти ребра ведут в разные листья. Если проводящее ребро записи предикатное, предикат, приписанный проводящему ребру, обязательно был вычислен перед тем, как мы попали в лист. Если проводящее ребро записи переключательное, то обязательно был вычислен переключатель, приписанный вершине, из которой исходит проводящее ребро. Причем такие переключатели для разных записей из Ju{x) будут разными, так как только одно из переключательных ребер, исходящих из одной вершины, может иметь проводимость, равную 1. Таким образом, каждой записи из Jij (x) можно сопоставить переключатель или предикат, вычисляемый непосредственно перед попаданием в соответствующий записи лист. Причем разным записям будут сопоставлены разные переключатели или предикаты. Отсюда следует, что Следовательно,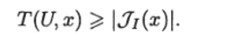

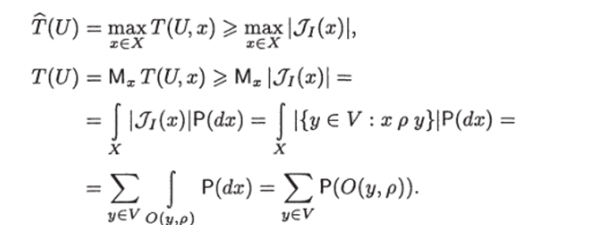
А так как это неравенство выполняется для любого графа U € то.

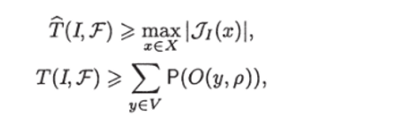
Так как в библиотеке V существует такая запись у, что 0(у, р) Ф = 0, то в любом ИГ, разрешающем ЗИП /, существует хотя бы одна цепь, и соответственно хотя бы одно ребро исходит из корня. Следовательно,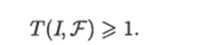

Тем самым теорема доказана.

В случае, когда базовое множество переключателей пусто, т. е. в случае ПИГ, этот результат относительно Т (/, J⁷) можно доказывать по-другому.

Если М — некоторое множество ребер некоторого ПИГ, то через Г (Л0 будем обозначать сумму сложностей ребер из Л/*.

Если U — некоторый ПИГ, а (3 — некоторая вершина ПИГ U, то через Afu, p будем обозначать множество ребер ПИГ С/, входящих в вершину р.

Лемма 2. Если S = (X, Y, р, а, Р) — некоторый тип задан информационного поиска, где X — множество запросов, У — множество записей, р — отношение поиска, заданное на X х Y, а — некоторая алгебра подмножеств множества X, Р — вероятностная мера на а, и U — некоторый ПИГ, разрешающий некоторую ЗИП I = {X, V, р) типа S, то для любой записи у 6 V справедливо

Доказательство. Возьмем произвольную запись у € V. Через В обозначим множество вершин, из которых исходят ребра, ведущие непосредственно в листья из Ьу (у), т. е. В — множество начал ребер ИЗ UА/и, а;

<*€Lu (y)

Так как ПИГ U разрешает ЗИП /, то согласно теореме 1.

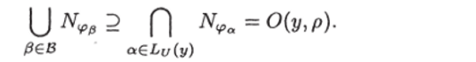
Из-за аддитивности меры Р.

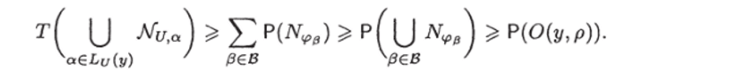
Тем самым лемма доказана.

Доказательство теоремы 4 для ПИГ.

Возьмем произвольный ПИГ U € U (I, T). Нетрудно заметить, что для любых у, у' (= V, таких, что у ф у справедливо.

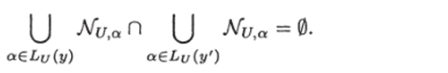
Тогда согласно лемме 2 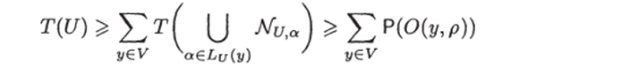для любой U Следовательно,.

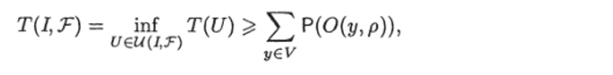
что и требовалось доказать.

С мощностной нижней оценкой непосредственно связано и понятие мгновенно решаемой задачи поиска, введенное в [27, 30, 157].

Под мгновенно решаемыми задачами поиска понимаются такие ЗИП, которые могут быть решены в среднем за время, необходимое на перечисление ответа, плюс некая не зависящая от размерности задачи константа. Здесь под размерностью задачи понимается объем библиотеки, в которой производится поиск.

Введенное таким образом понятие мгновенно решаемой задачи поиска нс может рассматриваться как строгое, и также как понятие алгоритма по версии А. Н. Колмогорова и В. А. Успенского [57] и А. А. Маркова [67], носит интуитивный характер, поскольку время здесь измеряется в некоторых элементарных операциях и тем самым предполагает некоторые «разумные» ограничения на множество элементарных операций. Если ничем не ограничивать множество элементарных операций, то всякая задача поиска становиться мгновенно решаемой. Этот факт доказывается в последней главе данной работы.

Упражнения

• 1.21. Пусть X = {1,2,…, ЛГ}, 5 = (X, X, =, Р, о) — тип поиска идентичных объектов, где а = 2^х, Р — равномерная вероятностная мера, т. е. для любого х? X выполняется Р (х) = 1/7V, V = {3,5,7,11,13,17,19}. Приведите мощностную нижнюю оценку для ЗИП I = (X, V, =).
• 1.22. Пусть Sdomi = ([0,1], [0,1], Р, а) — тип одномерной задачи о доминировании, где Р — равномерная вероятностная мера на [0,1], V = = {з/i, У2, ? • •, У к} Я [0,1]. Приведите мощностную нижнюю оценку для ЗИП

/ = .

1.23. Пусть Sint = {Xint, Yi_nt, Pint) «тип одномерного интервального поиска и на множестве запросов Х_|П» = {(«, v): 0 ^ ti ^ v ^ 1} задана равномерная вероятностная мера. V = {yi, y2* • • • уЗ/fc} Я [0,1]. Приведите мощностную нижнюю оценку для ЗИП / = (Xi_nt)V, pint) — Оцените сверху полученную величину.