Статически неопределимые фермы

Общие понятия

В гл. 3 были рассмотрены методы определения усилий в стержнях статически определимых ферм с помощью уравнений статики. Однако на практике часто применяются статически неопределимые фермы, для расчета которых недостаточно одних уравнений статики.

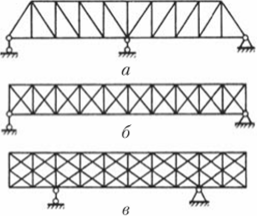
Рис. 7.1.

На рис. 7.1 показаны некоторые типы плоских статически неопределимых ферм. На рис. 7.1, а показана ферма на трех опорах, которая является статически неопределимой, так как для нее нельзя определить опорные реакции. В ферме на двух опорах, показанной на рис. 7.1, б, реакции в опорах легко найти, но усилия в стержнях определить нельзя. В этом случае ферма является статически неопределимой. Многорешетчатая ферма, изображенная на рис. 7.1, в, также является статически неопределимой.

В строительной практике могут применяться самые разнообразные типы статически неопределимых ферм, однако методы их расчета во всех случаях остаются неизменными.

Выбор основной системы и определение числа лишних неизвестных

В процессе расчета статически неопределимых ферм, так же как и балочных систем, выбирается основная система путем отбрасывания лишних связей и превращения заданной фермы в статически определимую систему. Эта задача в большинстве случаев решается легко. Необходимо строго следить за тем, чтобы полученная таким путем основная система была неизменяемой. В тех случаях, когда возникают затруднения, параллельно применяется аналитическая формула.

В гл. 3 при исследовании неизменяемости была получена формула С = 2У, где С — общее число стержней, включая и стерженьки опорных связей, а У — общее число узлов. Если в ферме имеются «лишние» стержни, то С > 2У; разница между С и 2У будет равна степени статической неопределимости.

Применим эту формулу для ферм, изображенных на рис. 7.1. Для фермы, показанной на рис. 7.1, а, число стержней, включая четыре опорных стерженька, будет С = 37 + 4 = = 41; число узлов У = 20; i = 41 — 2 • 20 = 1. Для фермы, изображенной на рис. 7.1, б, С = 51 + 3 = 54; У = 22; / = 54 — 22 • 2 = = 10.

Таким образом, степень статической неопределимости системы, изображенной на рис. 7.1, б, равна десяти. Отметим, что в местах пересечения раскосов последние не образуют узлов. При наличии скрепления раскосов, например с помощью болтов, степень статической неопределимости увеличивается. Для фермы, показанной на рис. 7.1, в, С = 54 + 20 = 74; У = 22 + 10 = 32; i = 74 — 2−32 = 10.

На рис. 7.2, а, б показаны фермы с шарнирными узлами, для которых степень статической неопределимости будет одинаковой. Возможные основные системы для этих ферм показаны на рис. 7.3. На схеме рис. 7.3, а в качестве лишних неизвестных приняты усилия в раскосах, а на схеме рис. 7.3, б за неизвестные приняты усилия в верхних поясах.

Для расчета статически неопределимых ферм чаще всего применяется метод сил. Исключением являются фермы с жесткими узлами, для расчета которых может успешно применяться метод перемещений.

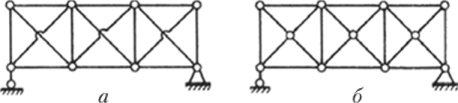
Рис. 7.2.

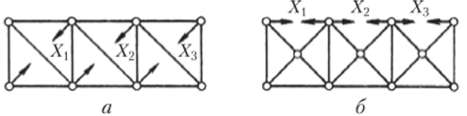
Рис. 73.