Собственные колебания системы с одной степенью свободы

Рассмотрим случай собственных колебаний, описываемых уравнением (15.6). Вначале проведем некоторые преобразования этого уравнения. Введем обозначения.

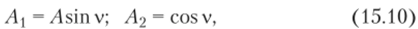
подстановка которых в уравнение (15.6) дает.

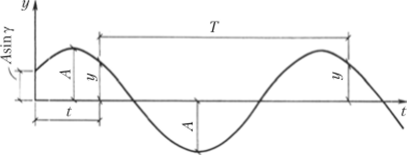
Рис. 15.13.

Полученное уравнение описывает движение балки при собственных колебаниях.

На рис. 15.13 изображен график синусоиды, представленной выражением (15.11). Синусоида в начале координат имеет ординату, равную Asm v, т. е. при t = 0 отклонение не равно нулю. Это явление обусловлено так называемым сдвигом фазы. Наибольшая ордината в синусоиде (15.11) равна А. Эта величина наибольшего возможного отклонения называется амплитудой; ее легко определить из выражений (15.10). Возведя в квадрат А и Л₂, получим.

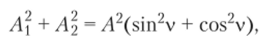
откуда, с учетом значений (15.7), найдем.

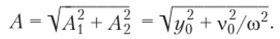
Таким образом, амплитуда зависит от начальных условий и частоты.

Поделив А на Л₂, по выражениям (15.10) с учетом равенств (15.7) получаем.

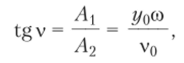
откуда.

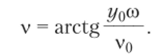
Из графика очевидно, что величина у меняет знак, следовательно, движение массы носит колебательный характер, масса т движется то вниз, то вверх и в определенные моменты достигает наибольших отклонений: А и -А. Время Г, за которое масса совершает один полный цикл, называется периодом колебаний. Его легко определить из условия, что при возрастании времени на Т величина у не изменяется, т. е.

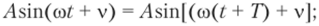
отсюда найдем.

Величина, обратная периоду колебаний, по физическому смыслу определяет число полных циклов колебаний в единицу времени:

В самом деле, один полный цикл происходит за Тсекунд, а за одну секунду число циклов будет в Т раз меньше. Величина п называется технической частотой.

Вернемся теперь к формуле (15.12). Величина со больше п в 2л раза, следовательно, она определяет собой также частоту колебаний, но только не в единицу времени, а в 2л единиц. Например, если п — число колебаний в секунду, то со — число колебаний в 2л секунд, поэтому условно называется круговой частотой колебаний. В дальнейшем будем величину со называть просто частотой колебаний.

Частота колебаний является одной из важных характеристик системы, она зависит от размеров и жесткостей системы и физических констант материала.

Из равенства (15.4) находим.

Для рассматриваемой системы, изображенной на рис. 15.12, при массе т_у прикрепленной к балке в середине пролета, будем иметь.

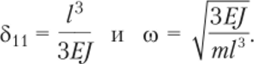
Из этого выражения очевидно, что чем больше масса т, тем меньше частота колебаний (больше период). Точно так же при увеличении пролета частота уменьшается, колебания происходят медленнее. При увеличении момента инерции сечения и модуля упругости происходит обратная картина: частота увеличивается, период уменьшается.

Рассмотрим теперь некоторые вопросы, связанные с существом явления.

Собственные колебания возникают в том случае, когда бачка каким-либо образом выведена из состояния покоя, например после встряхивания или какого-либо толчка. Из рис. 15.13.

очевидно, что по прошествии периода Тколебательный процесс не меняется, поэтому создается впечатление, что колебания будут продолжаться бесконечно долго. В действительности это нс так: собственные колебания постепенно затухают, амплитуда уменьшается, после некоторого времени колебания прекратятся и масса остановится. При решении задачи сделано допущение об отсутствии сил сопротивления, которые в действительности есть. В частности, имеет место сопротивление воздуха, которое при колебаниях сооружений невелико. Главные силы сопротивления возникают за счет внутреннего трения при деформации упругой системы. Для учета этих сил проводятся многочисленные эксперимен;

тальные исследования. С помощью записывающих приборов снимаются диаграммы колебаний, которые затем анализируются. На рис. 15.14 показан пример такой диаграммы.

Рис. 15.14.

Аналитическое решение этой

задачи, хорошо подтвердившееся экспериментами, показало, что амплитуда колебаний постепенно уменьшается по экспоненциальному закону. Как показано на рис. 15.15, верхняя и нижняя пунктирные линии имеют уравнения е^ЕЛ и e~^Et. В эти линии вписывается график изменения колебаний. Уравнение колебаний принимает вид.

Для определения величины, которая зависит от вязких свойств системы, замеряют амплитуды А_п и А_п+1, образовавшиеся в моменты времени t_n и t_n+_y отличающиеся на период Т. Тогда.

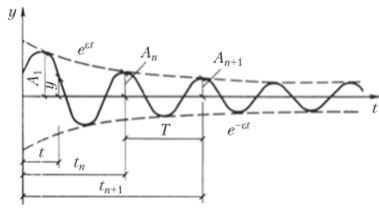
Величина у называется логарифмическим декрементом затухания. Она для разных материалов различна и часто зависит не только от материала, но и от конструктивного решения системы. Так, например, логарифмические декременты затухания для обычной железобетонной балки и для предварительно напряженной железобетонной балки тех же размеров будут различными.