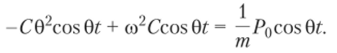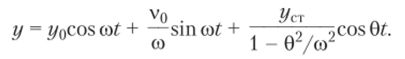Вынужденные колебания упругих систем
Заметим, что при 0/со 1 динамический коэффициент становится отрицательным. Объясняется это тем, что имеет место сдвиг фаз, т. е. закон изменения внешней силы не совпадает с законом движения массы т. Изменение направления действия силы произойдет несколько раньше, чем изменит направление движения масса т. Таким образом, внешняя сила на некотором отрезке времени тормозит движение массы. При очень… Читать ещё >
Вынужденные колебания упругих систем (реферат, курсовая, диплом, контрольная)
Рассмотрим теперь вынужденные колебания упругих систем при действии силы P (t)> изменяющейся во времени по гармоническому закону (15.1). Как уже установлено, они определяются третьим слагаемым равенства (15.9) у = = Ceos 0?, где С — амплитуда вынужденных колебаний. Для определения С подставим выражение (15.1) в дифференциальное уравнение (15.5). Учтя, что d2y/dt2 = -C02cos0?, получим.
Сократив все члены на cos 0?, найдем величину амплитуды С:
Подставив сюда вместо ее значение по (15.14) и учтя, что ЬРо есть статический прогиб у балки при условии, если вместо динамической силы (15.1) приложена ее амплитуда, будем иметь.
Из этой формулы очевидно, что амплитуда вынужденных колебаний от силы, изменяющейся по гармоническому закону, больше, чем прогиб, вызванный максимальным значением динамической силы, но приложенной статически.
Формулу (15.17) перепишем в виде.
где и — динамический коэффициент, равный.
На рис. 15.16 показан график изменения величины динамического коэффициента, взятого по абсолютной величине. При 0/со, стремящемся к единице, он быстро возрастает, а при совпадении частот колебаний (0/со = 1) обращается в бесконечность.
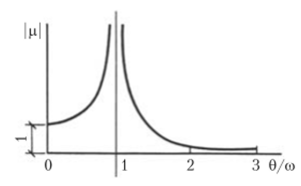
Рис. 15.16.
Выше упоминалось, что если не учитывать силы сопротивления, то получаемое решение будет приближенным. В действительности при совпадении частоты вынужденных колебаний с частотой свободных колебаний прогибы, а следовательно, напряжения в балке не обращаются в бесконечность, но они, как увидим в дальнейшем, достигают больших величин. Явление сильного нарастания амплитуд колебаний при совпадении частот носит название резонанса.
Резонанс опасен для сооружений, поэтому необходимо принимать меры для того, чтобы частоты собственных колебаний не совпадали с частотой вынужденных колебаний.
Заметим, что при 0/со 1 динамический коэффициент становится отрицательным. Объясняется это тем, что имеет место сдвиг фаз, т. е. закон изменения внешней силы не совпадает с законом движения массы т. Изменение направления действия силы произойдет несколько раньше, чем изменит направление движения масса т. Таким образом, внешняя сила на некотором отрезке времени тормозит движение массы. При очень большом отношении 0/со вынужденные колебания массы окажутся настолько малыми, что практически масса т перестает колебаться.
Вернемся к уравнению (15.9). Подставив в него значение амплитуды вынужденных колебаний С, получим.
Первые два члена описывают собственные, а третий член — вынужденные колебания. Собственные колебания быстро затухают, поэтому при стационарном движении останутся только вынужденные колебания, которые имеют ту же частоту, что и гармоническая сила.