Моделирование проблемных ситуаций с использованием метода аналитических сетей

Традиционно методология анализа иерархий и аналитических сетей, разработанная Т. Л. Саати, используется для разработки иерархической структуры, которая включает цель принятия решения, признаки (критерии) и альтернативы, которые задаются лицом, принимающим решение. Данная методология может быть, в частности, применена для разработки иерархической структуры условий принятия решения. При этом условия разбиваются на более детальные подусловия, которые могут быть связаны между собой. Результаты проверки (или возможные реализации) подусловий в совокупности формируют проблемные ситуации принятия решения¹.

В качестве вершины такой иерархической структуры выступает цель «Найти коэффициенты относительной значимости условий, подусловий и реализаций подусловий, учитываемых в задаче принятия решения».

В соответствии с методом анализа иерархий будем считать, что цель и уровни условий, располагающиеся под целью, составляют управляющую иерархию. При этом предполагается, что условия не зависят друг от друга.

Под каждым условием управляющей иерархии формируется сеть подусловий. Вид таких сетей зависит от сложности и содержания решаемой задачи^[1][2][3]. Возможные варианты сетей подусловий приведены на рис. 2.5.

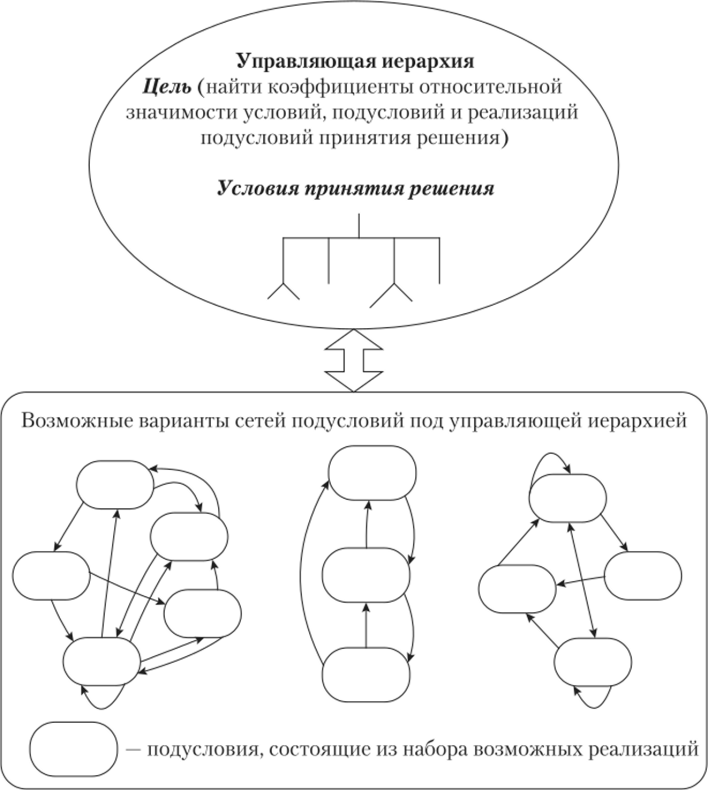
Рис. 2.5. Сетевая структура подусловий принятия решений^3.

Для обработки управляющей иерархии условий и вычисления коэффициентов их относительной значимости может быть использован метод анализа иерархий¹, а для расчета коэффициентов относительной значимости подусловий и их реализаций — метод аналитических сетей².

Определим коэффициенты относительной значимости условий в задаче принятия решения³.

Введем следующие условные обозначения:

U = (U_v …, U_w …, U_M), т = 1,…, М — условия принятия решения;

Р_тп — элементы матрицы парных сравнений относительной значимости условий, сформированные ЛПР, где т, п = ,…, М;

Z_co6cTB.м ⁼ (^гсобств. и •••> ^zco6ctb. м) ^— собственный вектор матрицы парных сравнений относительной значимости условий;

A,_{max ;}v/ ^— максимальное собственное значение матрицы парных сравнений относительной значимости условий;

W = (w_i9…, w_m, …, w_M) — вектор коэффициентов относительной значимости условий.

Оценки относительной значимости условий задаются в так называемой фундаментальной шкале Саати (табл. 2.12), состоящей из следующих возможных оценок: {1/9, 1/8, 1/7, 1/6, 1/5, ¼, 1/3, ½, 1, 2, 3, 4, 5, 6, 7, 8, 9}⁴. Связь оценок Р_тп и Р_пт выражается отношением: Р_пт = 1 / Р_тп Каждой градации шканты соответствует содержательное описание.

Таблица 2.12

Содержательная трактовка оценок матрицы парных сравнений Саати применительно к различным сущностям (условиям, подусловиям и их реализациям).

• 1 Саати Т. Л. Принятие решений. Метод анализа иерархий.
• 2 Саати Т. Л. Принятие решений при зависимостях и обратных связях. Аналитические сети.
• 3 Кравченко Т. К. Метод аналитических сетей при принятии решений в условиях неопределенности.
• 4 Саати Т. Л. Принятие решений. Метод анализа иерархий.

Заметим, что формируемые таким образом матрицы являются квадратными, обратно-симметричными и содержащими единицы на главной диагонали. Например, если Р_тп равно семи, то относительная значимость условия т «существенно выше» условия п. При этом значение Р_пт будет равняться 1/7, а это означает, что относительная значимость условия п «существенно ниже» условия т.

Рассмотрим процедуру нахождения коэффициентов относительной значимости условий, учитываемых в задачах принятия решений^[1].

• 1. Задаются условия принятия решения (вариант разработки нескольких уровней условий не рассматривается).
• 2. Формируются матрицы парных сравнений относительной значимости условий с элементами Р_тп, в которых оценивается относительная значимость условий т и п, где т, п= 1,…, М.
• 3. Для матрицы парных сравнений относительной значимости условий вычисляется собственный вектор Z_co6cm М⁼ (^собств. 1″ •••"^{собств.} •••> Z_cобств. м)> соответствующий максимальному собственному значению матрицы^[5]. Общий вид матричного уравнения для вычисления собственного вектора (из определения собственного вектора):

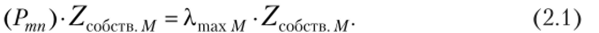
4. Элементы полученного вектора преобразуются согласно следующему правилу:

5. Вектор W = (w_v …, w_m, …, w_M) — искомый вектор коэффициентов относительной значимости условий, который впоследствии будет использоваться при вычислении коэффициентов относительной значимости подусловий принятия решения и их реализаций.

Определим коэффициенты относительной значимости подусловий принятия решения и их реализаций. После обработки управляющей иерархии необходимо обработать все сети, описывающие структуру подусловий принятия решения каждого условия.

Как уже было отмечено выше, вид таких сетей зависит от содержания решаемой задачи. Рассмотрим возможный вид сетевой структуры подусловий и их реализаций. Подобные сетевые структуры могут содержать зависимости следующих типов (рис. 2.6)^[1]:

• • тип /: зависимости подусловий от подцели (изображены сплошными стрелками, исходящими из подцели);
• • тип На. зависимости между двумя различными подусловиями и их реализациями (изображены пунктирными стрелками, исходящими из одного подусловия и входящими в другое);
• • тип ПЬ: взаимные зависимости между двумя различными подусловиями и их реализациями (изображены двумя разнонаправленными пунктирными стрелками, соединяющими два подусловия);
• • тип III. зависимости между реализациями одного подусловия (изображены пунктирными стрелками, исходящими из подусловия и входящими в то же подусловие).

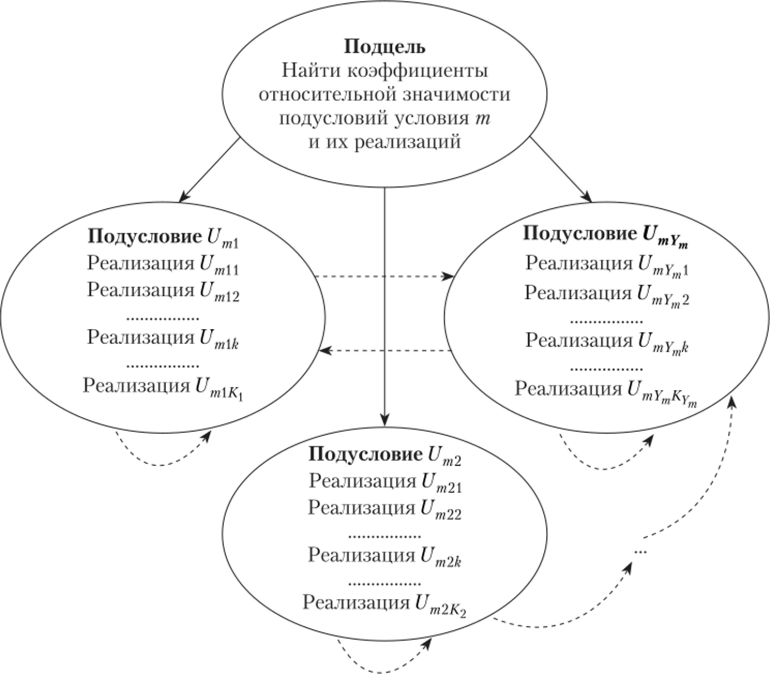
Рис. 2.6. Возможный вид сети нодусловий иод управляющей иерархией условий¹

Как было отмечено выше, для обработки данного вида сетей может применяться метод аналитических сетей, формализация которого применительно к новому объекту выглядит следующим образом:

U_my — подусловия г/, соответствующие условию т, где у = 1, …, Y_m; т = = 1, М;

— элементы матрицы парных сравнений относительной значимости подусловий у — U_т и t — U_mt относительно условия т, где уЛ- К У_т^[7]

Z_{co6crB m} — собственный вектор матрицы парных сравнений относительной значимости подусловий у относительно условия т> где т — 1, М;

А,[пах _т — максимальное собственное значение матрицы парных сравнений относительной значимости подусловий условия т, где т = 1, М;

w)_ny — вектор коэффициентов относительной значимости подусловий у условия т, где у = 1,Y_mm- 1,М.

Матрицы парных сравнений относительной значимости подусловий с элементами Р^_{у> t}) отражают зависимости типа I. Количество таких матриц равняется количеству условий, учитываемых в задаче принятия решений. Для иллюстрации приведем общий вид матрицы для зависимостей типа I (табл. 2.13).

Таблица 2.13

Общий вид матрицы парных сравнений относительной значимости подусловий условия т

Приведем условные обозначения для зависимостей типа 11а

U_mt — подусловия t условия т, влияющие на другие подусловия;

U — подусловия у условия т, подверженные влиянию других подусловий;

U_myk ~ реализации k подусловий у условия т, подверженные влиянию реализаций других подусловий, k = 1,…, К_у; у = 1,…, Y_rn; т = 1,…, М;

U_mth — реализации h подусловий t условия т, влияющие на реализации других подусловий, h = 1,…, K_t;t= 1,Y_m т = 1,…, М;

U_mtl — реализации / подусловий t условия ш, влияющие на реализации других подусловий, / = 1,…, К_с; t = 1,…, У_;"; т = 1,…, М;

_f и i) ~ ^{элемеиты} матрицы парных сравнений относительной значимости реализаций h и / подусловий t условия т, влияющие на реализации k подусловий г/, сформированные ЛПР;

Z^Te _w(/y о ^— собственные векторы матриц парных сравнений относительной значимости реализаций нодусловий t, влияющих на реализации подусловий у условия т

^шах т (и t)~ максимальные собственные значения матриц парных сравнений относительной значимости реализаций подусловий t, влияющих на реализации подусловий у условия т;

^wm (_y, t) ~ векторы коэффициентов относительной значимости реализаций подусловий t_y влияющих на реализации подусловий у условия т.

Зависимости типа IIа будут описаны таким количеством матриц парных сравнений относительной значимости реализаций h и / подусловий ?, какое.

число реализаций k содержится, а подусловиях у, подверженных влиянию подусловий t.

Для иллюстрации приведем общий вид матриц для зависимостей типа а (табл. 2.14).

Таблица 2.14

Общий вид матриц парных сравнений относительной значимости реализаций подусловий t, влияющих на реализации подусловий у

При наличии взаимозависимости между двумя различными подусловиями и их реализациями, которые изображены на рис. 2.6 двумя разнонаправленными пунктирными стрелками, помимо вышеуказанных матриц парных сравнений относительной значимости реализаций типа Па строятся дополнительные матрицы типа IIb (табл. 2.15).

Таблица 2.15

Общий вид матриц парных сравнений относительной значимости реализаций подусловий у, подверженных влиянию реализации подусловий t

Приведем условные обозначения для зависимостей типа II/?:

P^^b_h(p ц — элементы матриц парных сравнений относительной значимости реализаций к и / подусловий у условия т, подверженных влиянию реализаций h подусловий t;

^собств _{m (f} — собственные векторы матриц парных сравнений относительной значимости реализаций подусловий у условия т, подверженных влиянию реализаций h подусловий t;

^maxm (t, y) ~ максимальные собственные значения матриц парных сравнений относительной значимости реализаций подусловий у условия т, подверженных влиянию реализаций h подусловий t

~ векторы коэффициентов относительной значимости реализаций подусловий у условия т, подверженных влиянию реализаций h подусловий t.

Зависимости типа IIb будут описаны таким количеством матриц парных сравнений относительной значимости реализаций kill подусловий зу, какое количество реализаций h содержится в подусловиях t, влияющих на подусловия у (см. табл. 2.15).

Приведем условные обозначения для зависимостей типа III:

U_mt — подусловия t условия т, содержащие внутренние зависимости между реализациями;

U_mtk ~ реализации k подусловий t условия т, подверженные влиянию других реализаций этих же подусловий, где k = 1,…, K_t

U_mth, U_md — реализации h и / нодусловий t условия т, влияющие на реализации этих же подусловий, где Л, / = 1, …, K_t;

_k(U _v у — элементы матриц парных сравнений относительной значимости реализаций Ли/ подусловий t условия т, влияющих на реализации k подусловий V,

^соб_ств mt ~ собственные векторы матриц парных сравнений относительной значимости реализаций подусловий t условия т_у содержащих внутренние зависимости между реализациями;

^шах mt ~ максимальные собственные значения матриц парных сравнений относительной значимости реализаций подусловий t условия т w) l} — векторы коэффициентов относительной значимости реализаций подусловий t условия т.

Зависимости типа III описываются таким количеством матриц парных сравнений относительной значимости реализаций h и /, влияющих на реализации k, какое количество реализаций содержится в подусловиях t, имеющих внутренние зависимости. Для иллюстрации общий вид таких матриц приведен в табл. 2.16.

Таблица 2.16

Общий вид матриц парных сравнений относительной значимости реализаций нодусловий t, имеющих внутренние зависимости между реализациями.

Введем дополнительные условные обозначения для нахождения результирующих коэффициентов относительной значимости реализаций подусловий условия т:

SrnSuperMatr ~ суперматрица (общая композиция всех найденных векторов коэффициентов относительной значимости реализаций подусловий принятия решения условия га);

^rnSuperMatr ~ предельная суперматрица (суперматрица, многократно умножаемая сама на себя);

^wmyk ~ искомые векторы коэффициентов относительной значимости реализаций подусловий принятия решения условия га.

Выделим основные исходные данные для итогового решения поставленной задачи:

U_ту — подусловия принятия решений, соответствующие условию га, где т= 1,Му= 1,Y_m;

U _к — реализации к подусловий у условия га;

^т (у, t)' mth^mtf)" ^U_mfk № тук"^ myl)" mth^mti) ЭЛвМеНТЫ M3T;

риц парных сравнений всех типов, сформированные ЛПР в шкале Саати.

Опишем результирующую процедуру нахождения коэффициентов относительной значимости реализаций подусловий принятия решения условия га^[1].

• 1. Формируются исходные данные задачи.
• 2. Для нахождения коэффициентов относительной значимости подусловий принятия решений формируются матрицы парных сравнений с элементами _ty в которых оценивается относительная значимость подусловий принятия решений условия га.
• 3. Для матрицы парных сравнений относительной значимости подусловий принятия решений условия га вычисляется собственный вектор 2^обс_{ТВ т}, соответствующий максимальному собственному значению матрицы^{1[9]. Общий вид матричного уравнения для вычисления собственного вектора (из определения собственного вектора):}

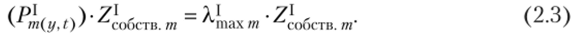
4. Для того чтобы получить коэффициенты относительной значимости подусловий, элементы полученного вектора преобразуются согласно следующему правилу:

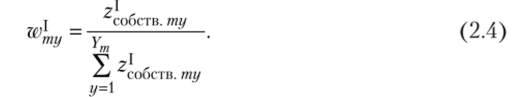
• 5. Для нахождения коэффициентов относительной значимости реализаций подусловий формируются матрицы парных сравнений с элементами ^Pu^X:_yS^U^U_md), P™_h(U_myk, U_mi/l), P™_k{U_mth, U_mtl).
• 6. Для всех матриц парных сравнений относительной значимости реализаций подусловий вычисляются собственные векторы Z^_{CTB m (l/ t}y ^собств.m (t, y) ^{исобств.} mt* соответствующие максимальным собственным значениям матриц^[10].

Из определения собственного вектора следует:

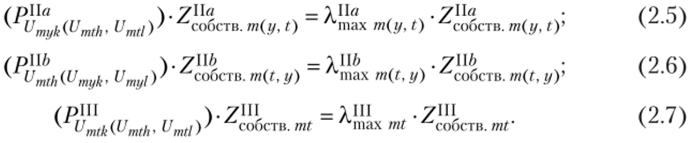
7. Через полученные собственные векторы находятся элементы векторов коэффициентов относительной значимости реализаций:

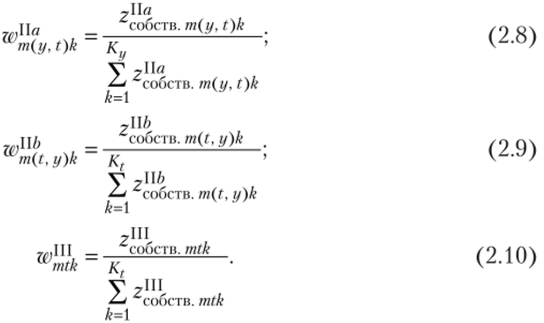
8. Все векторы, полученные в пунктах 4 и 7, группируются в суперматрицу S_mSuperMatr общий вид которой представлен в табл. 2.17.

Заполнение блоков суперматрицы осуществляется согласно следующим правилам:

• • вектор коэффициентов относительной значимости подусловий у условия т w)_ny служит для взвешивания блоков суперматрицы;
• • векторы коэффициентов относительной значимости реализаций ty ^wm{t. у) Р^{асположены 13} блоках, находящихся не на главной диагонали. При этом выполняются следующие условия:
• — при наличии зависимости между двумя различными подусловиями и их реализациями (зависимости типа Нс/) заполняется только один соответствующий блок суперматрицы. Блок, симметричный ему относительно главной диагонали, будет содержать нули. В табл. 2.17 этот случай проиллюстрирован блоками (2.1) и (2.2);

при наличии взаимозависимости между двумя различными подусловиями и их реализациями (зависимости типа IIа и 116) заполняются два соответствующих блока, располагающихся симметрично относительно главной диагонали. В табл. 2.17 этот случай проиллюстрирован блоками (4.1) и (4.2).

• векторы коэффициентов относительной значимости реализаций w^[_n)} расположены в блоках на главной диагонали. В табл. 2.17 этот случай проиллюстрирован блоком (3). При этом если у подусловия отсутствуют внутренние зависимости, то соответствующий блок будет содержать нули. В табл. 2.17 этот случай проиллюстрирован блоком (1).

Таблица 2.17

Общий вид суперматрицы.

• 9. Суперматрица S_mSuperMatr возводится в предельную степень (вычисляются произведения суперматрицы на саму себя) до тех пор, пока результат не стабилизируется¹.
• 10. Значения w_myk искомых коэффициентов относительной значимости реализаций подусловий условия т будут рассчитаны^[11][3] в предельной суперматрице S'" §_uperMatr.

Подобный расчет коэффициентов относительной значимости реализаций подусловий проводится для каждого условия ш, где т = 1,…, М.

Под проблемной ситуацией будем понимать совокупность отдельных реализаций всех выделенных подусловий условий принятия решения. Каждая проблемная ситуация должна содержать ровно по одной реализации из каждого подусловия каждого условия.

Наличие логического отношения «И» между отдельными реализациями позволяет складывать оценки относительной значимости отдельных реализаций выделенных подусловий рассматриваемых условий, формирующих данную проблемную ситуацию.

При большом количестве условий и подусловий принятия решения, а также их возможных реализаций количество проблемных ситуаций будет очень велико. С учетом того, что в каждой проблемной ситуации эксперт должен задавать оценки альтернатив по различным признакам, трудоемкость решаемой задачи может быть неоправданно высокой. Поэтому обычно рассматривается не более шести-восьми проблемных ситуаций, имеющих наиболее высокие коэффициенты относительной значимости.

• [1] Кравченко Т. К. Метод аналитических сетей при принятии решений в условиях неопределенности.
• [2] Caamu Т. Л. Принятие решений при зависимостях и обратных связях. Аналитическиесети. М.: ЛЕНАНД, 2015.
• [3] Там же.
• [4] Кравченко Т. К. Метод аналитических сетей при принятии решений в условиях неопределенности.
• [5] Caamu Т. Л. Принятие решений. Метод анализа иерархий.
• [6] Кравченко Т. К. Метод аналитических сетей при принятии решений в условиях неопределенности.
• [7] Саати Т. Л. Принятие решений при зависимостях и обратных связях. Аналитические сети.
• [8] Кравченко Т. К. Метод аналитических сетей при принятии решений в условиях неопределенности.
• [9] Caamu Т. JI. Принятие решений. Метод анализа иерархий.
• [10] Саати Т. Л. Принятие решений. Метод анализа иерархий.
• [11] Саати Т. Л. Принятие решений при зависимостях и обратных связях. Аналитические сети.
• [12] Там же.