Принятие решений с использованием принципов Парето и большинства и оценок альтернатив, заданных в порядковой шкале

Данный метод предназначен для согласования экспертных оценок альтернатив на основе принципов Парето и большинства, с позиций различных признаков в различных проблемных ситуациях. При этом экспертные оценки рассматриваемых альтернатив задаются в порядковой (ранговой) шкале. Обозначение метода в ЭСППР — PRT, PUR_r

В качестве возможных вариантов решения рассматривается набор из I альтернатив X = (X, Х₂,…, X,…, Х,)_} i - 1, 2,…, /.

Решение принимается при наличии J проблемных ситуаций 5 = (5^ S₂, …, S,…, Sr), j= 1,2,Каждая из проблемных ситуаций появляется с веро;

./.

ятностью Pj , j = 1, 2, …J, ?Pj = 1.

j=i

Каждая из альтернатив характеризуется L признаками. Каждый признак.

L

имеет коэффициент относительной значимости Z/, / = 1, 2,…, I, ?Z/ = 1.

ы Для оценки альтернатив привлекаются D экспертов. Каждому из экспертов присваивается коэффициент компетентности XV_d, d = 1,2, …, Д.

iw_d=.

d=l.

Каждый из экспертов оценивает каждую альтернативу по каждому признаку в каждой из возможных проблемных ситуаций. Оценка производится в порядковой шкале, т. е. чем предпочтительнее альтернатива — тем меньше ранг, присваиваемый экспертом. В результате формируется набор матриц предпочтений, каждая из которых имеет размерность I х L, где / — количество возможных вариантов решения (альтернатив), L — число признаков сравнения. Элемент матрицы предпочтений F_j/dj представляет собой оценку варианта решения X, d-м экспертом с позиций /-го признака в j-й проблемной ситуации, заданную в порядковой шкале (г = 1, 2,…, 1,1= 1, 2,…, L, d = = 1,2, … D;j= 1, 2,…,)).

Алгоритм решения задачи предусматривает выполнение следующих шагов.

Шаг 1. Попарное сравнение альтернатив. В соответствии с принципом Парето, используемым для согласования предпочтений, задаваемых экспертом d в различных ситуациях j с позиций нескольких признаков /, альтернатива X, предпочтительнее альтернативы Х_к, если:

• • по мнению всех экспертов d (d= 1,2,…, D) во всех проблемных ситуациях j (j = 1, 2,…, J) с позиций всех признаков / (/= 1, 2,…, L) выполняется неравенство F_ddj < F_k/dj, т. е. альтернатива X, не хуже альтернативы Х_к;
• • имеется хотя бы один эксперт q (q = 1,2,D), по мнению которого хотя бы в одной ситуации h (h = 1, 2, …, J) хотя бы по одному признаку t (t = 1, 2, …, L) выполняется неравенство F_itqh < F_ktqh, т. е. альтернатива X, лучше альтернативы Х_к.

В случае выполнения перечисленных условий для некоторых пар сравниваемых альтернатив, худшие альтернативы из этих пар помечаются как «нежелательные».

Шаг 2. Определение альтернатив, входящих в состав множества Парето. На данном шаге альтернативы, помеченные как «нежелательные» в результате попарных сравнений, исключаются из рассмотрения. Оставшиеся альтернативы X, — являются элементами множества Парето (/ = 1, 2,…, Г, где Г — количество альтернатив, вошедших в состав множества Парето). Любая из альтернатив множества Парето предпочтительнее любого из отброшенных вариантов, сами же элементы множества Парето несравнимы между собой.

Шаг 3. Формирование матриц парных сравнений для альтернатив множества Парето. На данном шаге для альтернатив Х_;, являющихся элементами множества Парето (г = 1, 2, …, /'), формируются матрицы парных сравнений, в которых попарно сопоставляются все альтернативы по каждому признаку, в каждой ситуации, на основе оценок, заданных каждым экспертом. Элементы матриц парных сравнений (г, к = 1, 2,…, /*; /= 1, 2,…, L;d= 1, 2,…, D, j = 1, 2, …, J) для всех возможных пар рассматриваемых альтернатив определяются на основе оценок всех экспертов по всем признакам во всех проблемных ситуациях следующим образом:

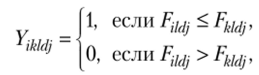
где Рщ — элемент матрицы предпочтений, заданный в порядковой шкале d-м экспертом для г-й альтернативы, по /-му признаку, ву-й проблемной ситуации (г = 1, 2,…, Г; I — 1,2,…, L;d = 1,2,…, D; j = 1, 2,…,./);

Рщ — элемент матрицы предпочтений, заданный в порядковой шкале d-м экспертом для А'-й альтернативы, по /-му признаку, в у-й проблемной ситуации (k = 1, 2,…, Г; 1= 1, 2,…, L; d = 1, 2,…, D; j = 1, 2,…, J).

Шаг 4. Формирование обобщенной матрицы для альтернатив, входящих в состав множества Парето. Элементы обобщенной матрицы B_ik (г, k = 1,2,…, Г) для всех возможных нар альтернатив, входящих в состав множества Парето, в соответствии с принципом большинства определяются следующим образом:

где Ущ — элемент матрицы парных сравнений для г-й и /г-й альтернатив по /-му признак}', в j-й проблемной ситуации, на основе оценок d-ro эксперта (г, k = 1, 2,…, Г, 1=1, 2,…, L; d = 1, 2,…, D;j = 1, 2,…,/);

Pi — вероятность появления j-й проблемной ситуации (j = 1, 2,.

ZI — коэффициент относительной значимости /-го признака (/=1,2,…, I);

W_(/ — коэффициент компетентности d-го эксперта (d = 1,2,…, ?)).

Шаг 5. Формирование медианной матрицы для альтернатив множества Парето. Элементы медианной матрицы Y_tl (i, k = 1, 2,Г) для всех возможных пар альтернатив множества Парето определяются следующим образом:

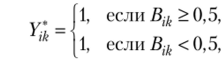
где B, j, — элемент обобщенной матрицы для г-й и k-й альтернатив (г, k = 1, 2, Г).

Шаг 6. Определение коэффициентов предпочтительности альтернатив множества Парето. На данном шаге для всех рассматриваемых альтернатив множества Парето определяются коэффициенты предпочтительности Ej (i = 1, 2,Г). Эти коэффициенты рассчитываются по формуле.

где Y'_k — элемент медианной матрицы для г-й и k-й альтернатив (г, k = 1, 2,.

Шаг 7. Ранжирование альтернатив множества Парето. На данном шаге альтернативы множества Парето упорядочиваются по убыванию коэффициентов предпочтительности E_t (г = 1, 2, Г). Альтернатива с наибольшим значением коэффициента Ej считается наиболее предпочтительной и получает ранг 1, альтернативе со вторым, но величине значением коэффициента Ej присваивается ранг 2 и т. д.