Примеры синтеза логических автоматов

На рассматриваемых ниже задачах синтеза еще раз оценим возможность изучаемого аппарата преобразования логических функций в целях построения минимальной логики.

Многофункциональные автоматы. В отличие от предыдущих задач, здесь речь идет об автоматах не с одним, а с несколькими выходами. Ранее при изучении одноразрядных сумматоров (см. таблицы истинности на с. 90, 92) мы уже имели дело с двумя выходами — s (сумма) и р (перенос).

Если у автомата на п входов имеется р выходов, каждый из которых подчиняется своей логической функции.

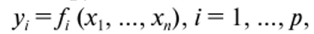
то такой автомат в принципе эквивалентен р самостоятельным автоматам. Если каждый автомату, имеет к, импликант при записи функции в ДНФ, то общее число элементов И будет составлять.

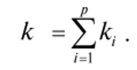
Поскольку для реализации дизъюнкции в каждом автомате необходим элемент ИЛИ, то их общее количество ?_или = р. Общее количество элементов И и ИЛ И составляет к = к_и + к_иш. Например, у автомата на 4 входа а, />, с_у d есть две функции:

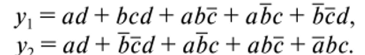
Нетрудно видеть, что к_и = 10, ?_или = 2, к = 12. Однако если для каждой из функций заполнить свою карту Карно, то можно обнаружить общие поля, которым соответствует некоторая функция Я. Эту функцию целесообразно использовать при синтезе каждой из функций у

На рис. 30 показаны карты для у, и у₂, общая составляющая часть Я заштрихована.

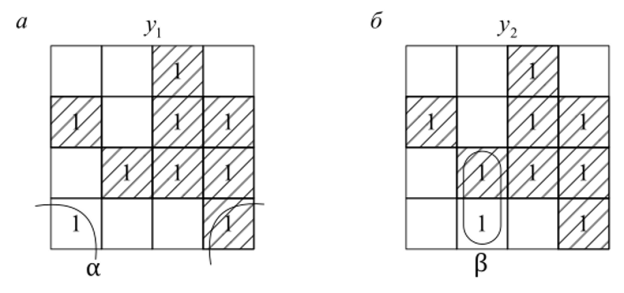
Рис. 30. Карты Карно для функций у, (я) и у₂ (б).

В соответствии с методом Карно можно записать.

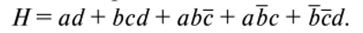
С учетом общей части Я каждая функция может быть представлена как.

Общее число логических элементов в системе (19).

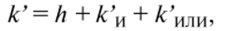
где И — число элементов в структурной схеме Я.

Если к' < ку то выгоднее перейти к моделированию функций через выражение (19).

Для нашего примера ср, = bed (контур а), ср₂ = abc (контур |3), следовательно,.

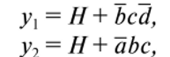
при этом И = 6, к'_и = 2, к'_или = 2, к'= 10. Поскольку к'< 12, то имеет смысл воспользоваться структурной схемой, показанной на рис. 31.

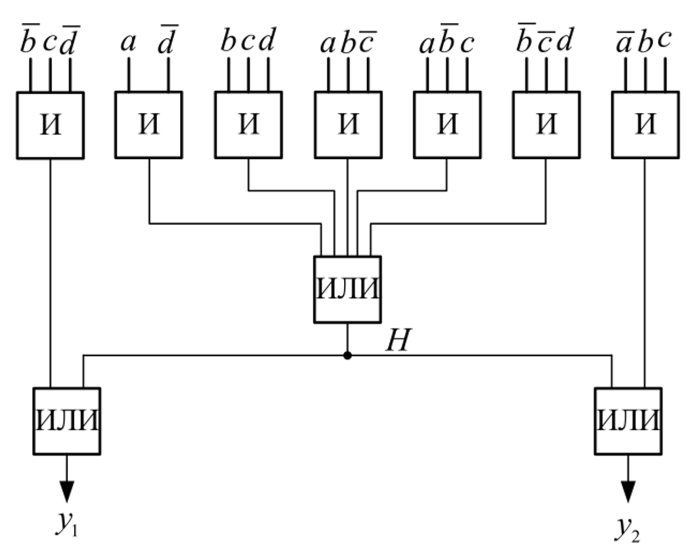
Рис. 31. Автомат с двумя выходами у, и у₂

Реализация логической функции на базе мультиплексора. Мультиплексор (МП) — это цифровой многопозиционный переключатель, подругому — коммутатор. Один из п входов с номером j коммутируется на единственный выход V, если на адресное управление s подано двоичное число j. На рис. 32 показано условное отображение МП с 8 входами (от 0 до 7), имеющими соответственно адресные номера 000, 001,010 и т. д. до 111. Размерность s равна 3, что позволяет задавать адрес входа j в виде минтерма т_}.

Например, если требуется закоммутировать шестой вход, то s = ПО, иначе s = abc, при этом V= в₆ Информация на входе в₆ (1 или 0) повторяется на выходе V. Эта информация может быть не только в виде одного сигнала, но и в виде последовательности дискретных сигналов, а также в виде аналогового сигнала. В нашей комбинаторной задаче будем рассматривать в, как двоичный сигнал (0 или 1). Таким образом, при 5=110 имеем V— ъ_ь-аЬс = в₆/и₆, где т_ь — шестой минтерм. В целом с учетом того, что МП может коммутировать любой вход, можно записать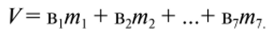

Нетрудно видеть, что МП можно использовать для реализации логической функции, записанной в СДНФ.

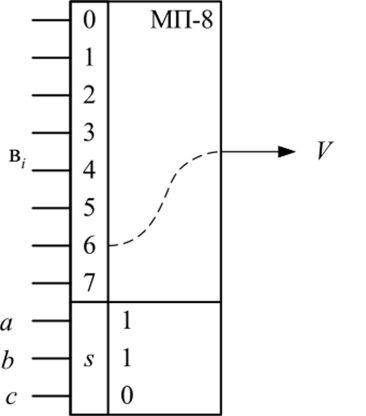
Рис. 32. Восьмиразрядный мультиплексор.

Рассмотрим пример. Требуется синтезировать устройство, сигнализирующее о работе энергетического комплекса, состоящего из трех агрегатов а, Ь, с. Нормальное состояние — в работе находится не менее двух агрегатов (/;,), в противном случае — аварийный сигнал/_v Соответствующая таблица истинности (рис. 33) отражает поставленное условие. Естественно, f_a =/,.

Поскольку в этом случае V= 1 т_ъ + 1 т₅ + 1 т_ь + 1 т_ъ достаточно на 3-й, 5-й, 6-й и 7-й входы подать питание, чтобы обеспечить состояния входов в₃ = в₅ = в₆ = в₇ = 1, то МП, показанный на рис. 29, будет действовать согласно таблице истинности и логической формуле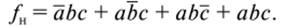

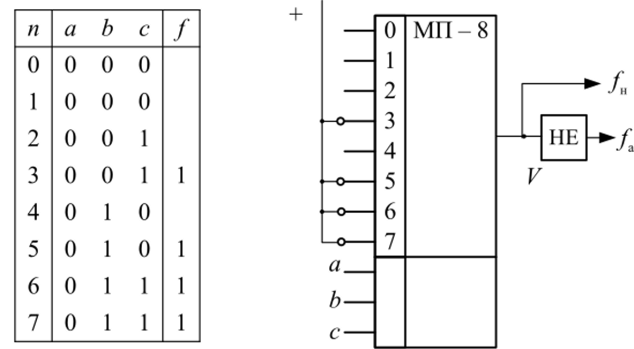
Рис. 33. Реализация функции/_н на МП.

Кодирующие и декодирующие устройства. Во многих информационных системах, в том числе вычислительной технике, телемеханике и АСДУ ЭЭС, используется преобразование информации. Чаще всего речь идет о преобразовании двоичных чисел в другую запись, например в код Грея, код Хэмминга и др. Естественно, возникает необходимость возврата из этих записей (кодов) к двоичному виду. Поскольку в своей деятельности человек использует множество цифр и символов различных языков, объединяемых в тот или иной информационный алфавит, то возникают задачи кодирования и декодирования этих символов. Например, нажимая на обычном калькуляторе кнопку одной из цифр десятичной записи, мы получаем отображение этой цифры на жидких кристаллах в виде семисегментного кода. Часто преобразователи кодов называются шифраторами и дешифраторами. Поскольку в двоичной логической технике используется только два символа — 0 и 1, то элементы исходного алфавита а, а₂, …, а,…, а," представляются при вводе в кодирующее устройство КУ (рис. 30, а) как единица на входе с номером /, т. е. как 00 … I … 0. Функция устройства преобразования заключается в получении на т выходах комбинации 1 и 0, однозначно соответствующей поданному сигналу с номером /. Чаще всего эта комбинация есть двоичное число. Если т = 256, то п — 8, так как восьмиразрядным двоичным числом можно отобразить т входных символов. Например, нажимая на клавиатуре элемент а₁₃₇, получим число 10 001 001. На рис. 34, а показано КУ на 16 входов (от 0 до 15) и 4 выхода для получения двоичных чисел от 0000 до 1111. При / = 3 получаем 0011.

Задача декодирования состоит в получении сигнала «1» на выходе /, если на входы 0 … 2″ ^-1 подана комбинация 0 и 1, соответствующая двоичному числу/. На рис. 30, б показан случай, когда входное число 0101₍₂₎ декодируется в сигнал на выходе / = 5.

Иногда приходится переводить информацию из одной системы кодирования в другую, например из кода Грея в двоичную систему. Таким образом, устройства преобразования информации являются типичными примерами многофункциональных логических автоматов.

Рассмотрим задачу получения кода Хэмминга. Как известно, при передаче информации в канале связи из-за внешних помех может произойти искажение сигнала так, что 1 будет восприниматься на приемном конце как 0 и наоборот. Например, при передаче двоичного числа 1000 будет получено, допустим, число 1010. По внешнему виду никоим образом невозможно судить о достоверности информации. Если же исходное двоичное слово (обозначим его разряды как abed) дополнить контрольным разрядом х, формирование которого подчиняется логической формуле х = а ®Ь ®с ®г/, то в кодовой комбинации xabed всегда будет четное число единиц.

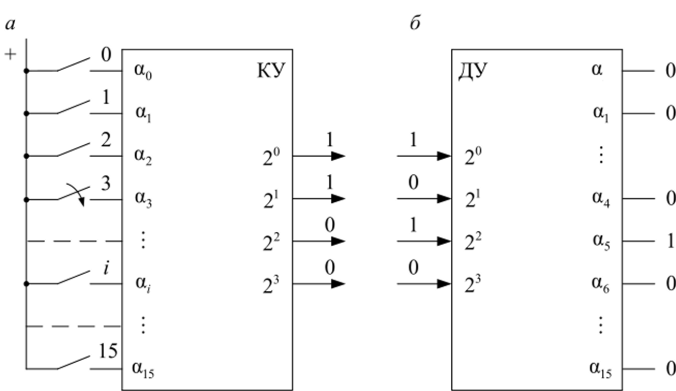
Рис. 34. Кодирующее (а) и декодирующее (6) устройство В нашем примере отправляемое число есть 11 000, и если на приемной части получено число 11 001 с нечетным числом единиц, то можно сделать однозначный вывод о наличии искажения информации, не выявляя при этом разряд с искажением сигнала. Более сложный код Хэмминга позволяет не только установить факт появления ошибки, но и указать тот разряд, в котором требуется восстановить сигнал, т. е. произвести его инверсию. Для этого вводятся дополнительно три разряда х, х₂, х₃, и код приобретает вид х_хх₂ах₃bed. Таким образом, четырехразрядный код переводится в семиразрядный, в котором дополнительные переменные вычисляются по логическим формулам.

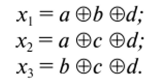
На элементной базе М2 — «сложения по модулю 2» (операция неравнозначности) — схема приобретает вид, показанный на рис. 35. Легко перейти к базису «И—ИЛИ—НЕ», если вспомнить, что ab = аЪ + ab. Тогда в этом базисе получим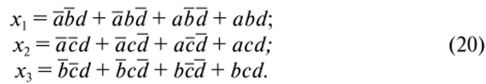

Поскольку в формировании переменных х, х₂, х₃ используются трехразрядные минтермы, постольку получение этих переменных может быть выполнено на восьмиадресных мультиплексорах (рис. 36) с трехразрядным адресным управлением. В каждом из мультиплексоров питание подается на входы 0, 2, 4, 7, так как именно эти минтермы фигурируют в формулах (20).

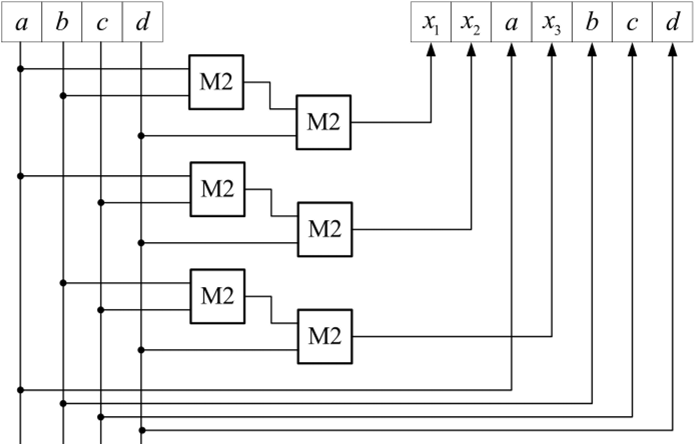
Рис. 35. Получение кода Хэмминга.

Для синтеза декодирующего устройства на приемном конце канала связи воспользуемся логическими формулами.

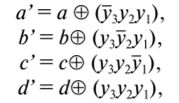
обеспечивающими инверсию одного из входных сигналов (a, b, с, d) в результат декодирования a', b с d если в соответствующем разряде произошло искажение сигнала, и сохранение сигнала (например, а' = а), если искажения не было.

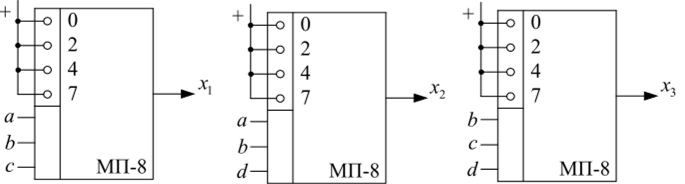
Рис. 36. Получение дополнительных разрядов в коде Хэмминга на мультиплексорах.

При этом дополнительные переменные вычисляются (формируются) согласно формулам.

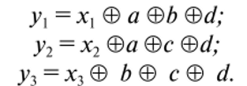
Пусть искажение произошло в шестом разряде кода Хэмминга, т. е. в значении с, тогда у_х = 0; у₂ = 1; у_ъ = 1;

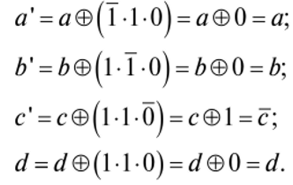
Реализация структурной схемы декодирования на той или иной элементной базе не представляет затруднений.